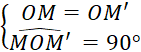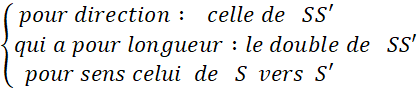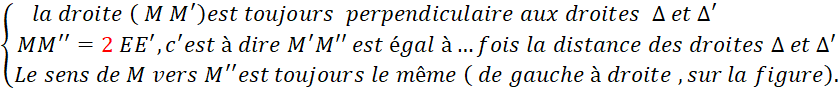Programme de troisième Collège.
Fiches sur la COMPOSITION DE TRANSFORMATION.
	Fiche 1 : Image de figures usuelles par des transformations.
	Fiche 2 : Rotation.
	Fiche 3 : Composition de deux symétries centrales.
	Fiche 4 : Composition de deux symétries orthogonales d’axes parallèles.
	Fiche 5 : Composition de deux symétries orthogonales d’axes perpendiculaires.
	Fiche 6 : Composition de translation.( et somme de vecteurs)
		Aller au corrigé …….
Pré requis:
Les transformations géométriques (liste)

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent 1°) Déplacement . 2°) voir le cours résumé sur les transformations géométriques.

Objectif suivant 1°) translation 2°) rotation 3°) rotation et translation conjuguées 4°)les propriétés des transformations géométriques

tableau liste « géométrie plane » Les tracés géométriques

		Rappels :
		LES TRANSFORMATIONS GEOMETRIQUES ( COMPOSITION ) :
Liste des transformations principales :
1°) Les divers « déplacements » :
	· Translation
	· Rotation
2°) les oppositions ou symétries, qui, en géométrie plane , sont des cas particuliers de déplacements.
	· Symétrie centrale
	· Symétrie orthogonale
3°) les divers modes de projections
	· Projection par rapport à une direction quelconque.
	· Projection orthogonale
4 °) l’homothétie
5°) la similitude

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

	Fiches sur la COMPOSITION DE TRANSFORMATIONS .
	Fiche 1 : Image de figures usuelles par des transformations.
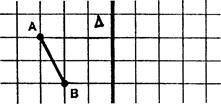
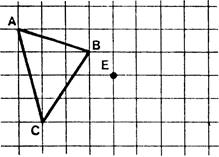
	Dans chacun des cas , symétrie orthogonale , symétrie centrale, translation , dessinez les images des figures données. Vous retrouvez ainsi certaines propriétés que vous avez étudiées dans les années passées.
	Symétrie orthogonale d’axe :	Symétrie centrale d’axe :	Translation de vecteur «  »
Droite
Segment
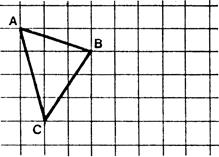
Triangle
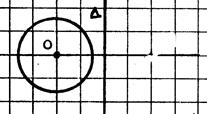
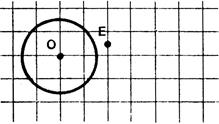
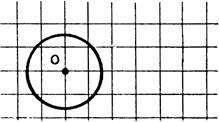
Cercle
Droites parallèles
Droites Perpendiculaires
Parallélogramme

Fiche 2 : Rotation.
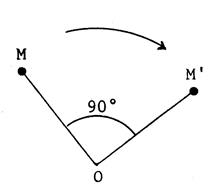
Rappel : Dire que le point « M’ » est l’image du point « M » dans la rotation de centre « O » et d’angle « 90° » c’est dire ( voir ci-contre)
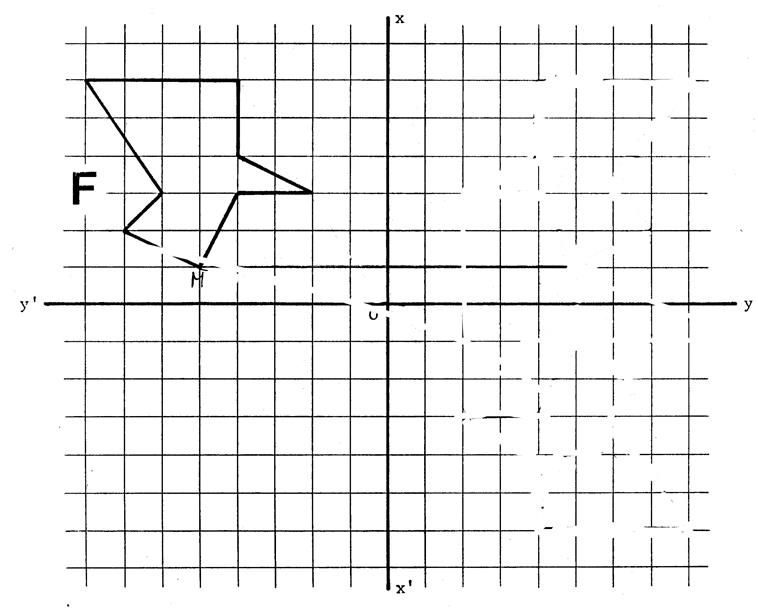
Activité 1 :
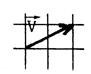
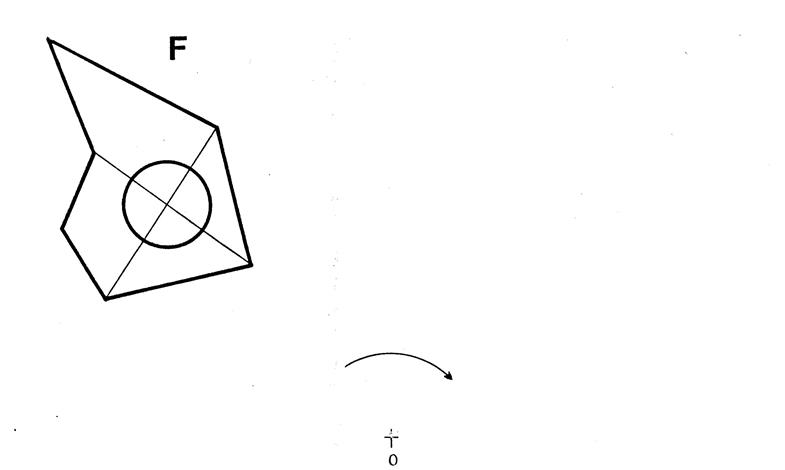
Dessinez l’image « F’ » de la figure « F » dans la rotation de centre « 0 » , d’angle « 90° » et dont le sens est donné par la flèche.
Activité 2 :
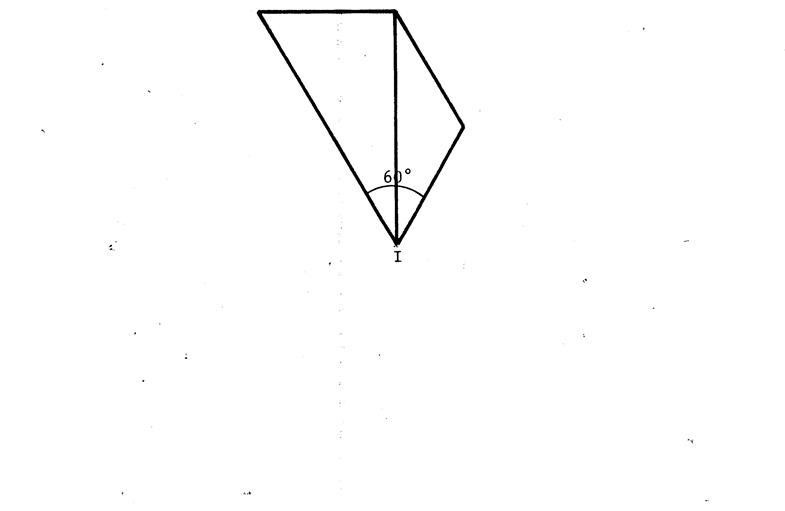
Dessinez l’image de la figure ci-dessous dans la rotation de centre « I » et d’angle « 60° » et recommencez avec l’image obtenue autant de fois qu’il faut pour que la dernière image coïncide avec la figure donnée. Vous obtenez alors une rosace que vous pouvez mettre en couleur comme il vous plaira.

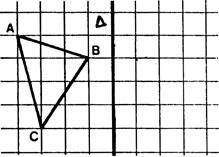
Fiche 3 : Composition de deux symétries centrales.

Activité :

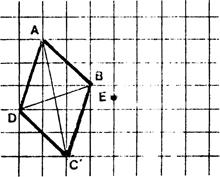
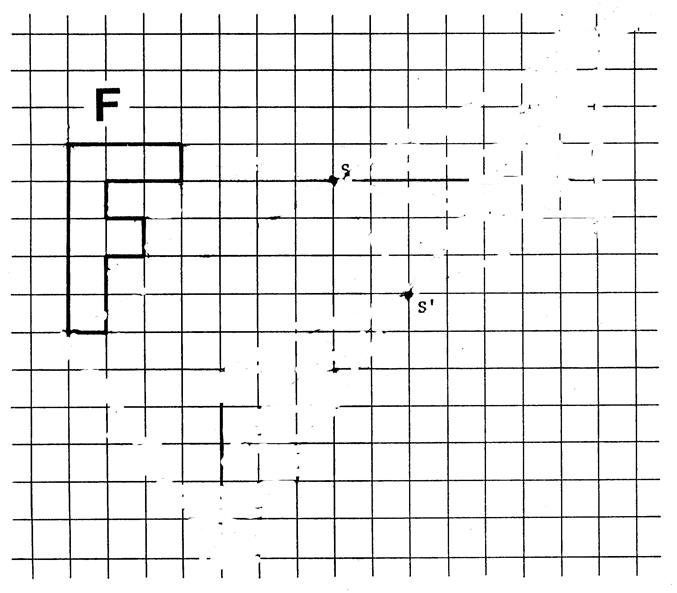
On donne deux points « S » et « S’ »et une figure « F ».

Dessinez l’image « F’ » de la figure « F » dans la symétrie centrale de centre « S » puis l’image de « F’’ »de la figure « F’ » dans la symétrie centrale de centre « S’ ».

Il semble que « F’’ » soit l’image de « F » par une « ………………………….. » .

C’est ce que nous allons démontrer.

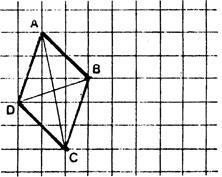
Ø Choisissez un point « M » quelconque de « F ».

Ø Placez sur « F’ » le point « M’ » symétrique de « M » par rapport à « S ».

Vous pouvez dire que « S » est le ……………….. de .

Ø Placez sur « F’’ » le point « MM’’ » symétrique de « M’ » par rapport à « S’ ».

Vous pouvez dire que « S’ » est le centre de .

Dans le triangle «  M M’ M’’ » , « (SS’) » est alors « droite des milieux ».

Vous en déduisez que :

On a ainsi déterminé un vecteur «  » qui a :

« S » et « S’ » étant des points fixes donnés le vecteur «  » est indépendant du choix de « M ».

Quel que soit le point « M » de « F » et son image « M’’ » sur « F’’ » , on a toujours :

La transformation qui fait passer de « F » à « F’’ » est donc une ………………………….. de vecteur

Ø Quand on applique à une figure une transformation suivie d’une autre transformation on dit que la transformation résultante est la composée de ces deux transformations.

Ø Ce qui a été démontré pour « F » est vrai pour tout autre figure. On énoncera alors le théorème suivant :

Théorème :

La composée de deux symétries centrales est une ………………………..

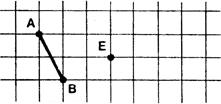
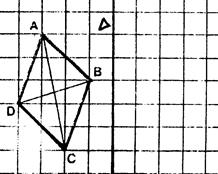
Fiche 4 : Composition de deux symétries orthogonales d’axes parallèles.

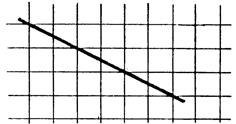
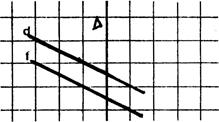
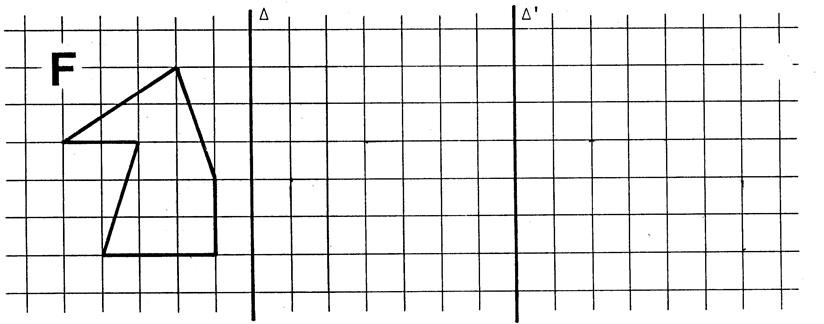
On donne deux droites «  » et «  » parallèles et une figure « F ».

Activité : On vous demande de dessiner l’image « F’ » de la figure « F » dans la symétrie orthogonale d’axe «  » puis l’image « F’’ » de la figure « F’ » dans la symétrie orthogonale d’axe «  »

Observation :

Il semble que « F’’ » soit l’image de « F » par une ..translation ..

C’est ce que nous allons démontrer ( dans le cas de la figure ci-dessus) .

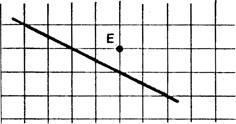
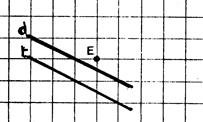
Ø Choisissez un point « M » quelconque de « F ».

Placez « M’ » symétrique de « M » par rapport à «  » . «  » est alors ……… …………….. de .

Appelons « E » le point d’intersection de ( M M ’) et «  » . « E » est alors …………….. de .

Placez « M ’’ » symétrique de « M ’ » par rapport à «  » . «  » est alors ………………… de .

Appelons « E ’  » le point d’intersection de ( M ’ M ’’) et «  » . « E ‘  » est alors ………………… de .

Démontrez verbalement que pour tout point « M » de « F » et son image «  M’’ » sur « F ‘’ »,

On a ainsi déterminé un vecteur qui a :

étant des droites fixes, le vecteur est indépendant du choix de « M ».

Quel que soit le point « M » de « F » et son image « M’’ » sur « F’’ », on a toujours

On passe donc de « F » à « F’’ » par une translation de vecteurs

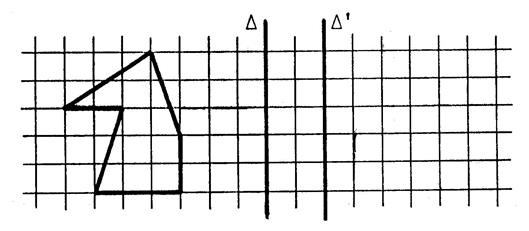
Attention :

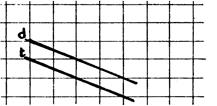
Les figures « F » , « F’ » , « F’’ » et les droites ne sont pas toujours disposées comme sur le dessin ci-dessus. IL existe plusieurs situations possibles . En voici une ci-dessous.

Dessinez les images « F’ » et « F’’ » et faites les mêmes constatations que précédemment.

Ø Quel que soit le cas de figure , il est possible de démontrer que :

Théorème :

La composée de deux symétries orthogonales d’axes parallèles est une ………………………..

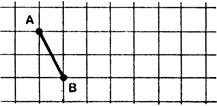
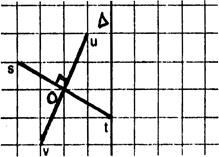
Fiche 5 : Composition de deux symétries orthogonales d’axes perpendiculaires.

«   » et «  » sont deux droites perpendiculaires sécantes en « O ».

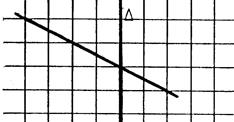
Dessinez l’image « F’ » de la figure « F » dans la symétrie orthogonale d’axe «   » puis l’image « F’’ » de la figure « F’ » dans la symétrie orthogonale d’axe «  ».

Il semble que « F’’ » soit l’image de « F » par . …………………………………………….. .

C’est ce que nos allons démontrer dans le cas de la figure ci-dessus.

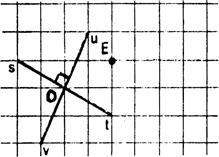
Ø Choisissons un point « M » quelconque de « F ».

Ø Placez le point « M ’ » symétrique de « M » par rapport à «   ».

( la demi-droite) est alors la bissectrice de l’angle «  » donc : «  »

Ø Placez le point « M ’’ » symétrique de « M’ » par rapport à «   ».

( la demi-droite) est alors la bissectrice de l’angle «  » donc : «  »

Démontrez verbalement que «  » , ce qui permet de dire que « M » , « O » et « M ’’ » sont …………………………..

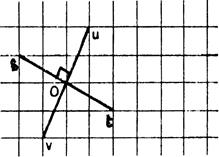
D’autre part , « O » étant le point d’intersection de «   » et de «   » , « O » est situé sur «   » donc « OM = …… » et « O » est situé sur «   » donc « OM ‘ = …… » donc « OM = …… ».

Puisque « M » , « O » , « M’’ » sont alignés et que «  OM = ……… » alors « O » est le ………………………… de

Et cela quel que soit le point « M » de « F » et son image « M’’ » de « F’’ ».

On passe donc de « F » à « F’’ » par une ……………………………… de centre « O ».

Ø Il existe d’autre cas de figure , mais il est toujours possible de prouver que :

Théorème :

La composée de deux symétries orthogonales d’axes perpendiculaires est une …………………………… dont le centre est le point d’intersection des axes de symétrie.

Fiche 6 : Composition de translation.	VOIR LA FICHE :
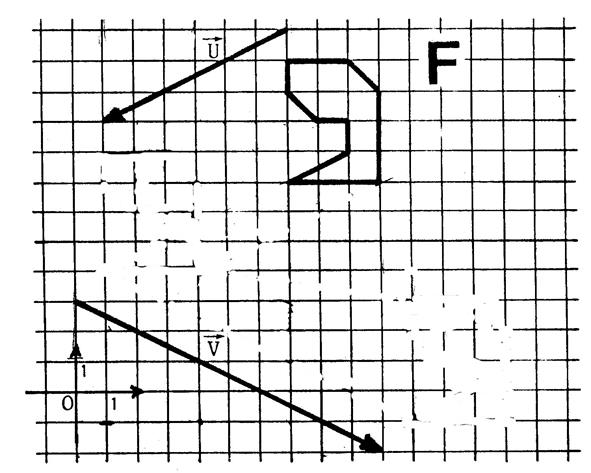
Ci-dessous : Dans le plan muni d’un repère , on donne deux vecteurs et et une figure « F ».
On vous demande de dessiner l’image « F’ » de la figure « F » dans la translation de vecteur puis l’image « F’’ » de la figure « F’ » dans la translation de vecteur .
Observation : Il semble que « F’’ » soit l’image de « F’ » par une ………………………………………….. Dessinez près de « F » et « F’’ » un représentant du vecteur de cette translation.