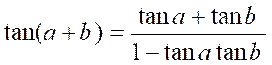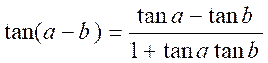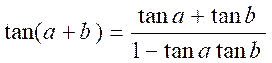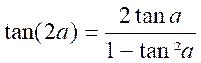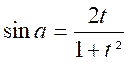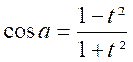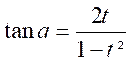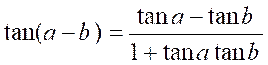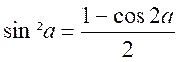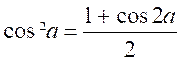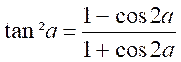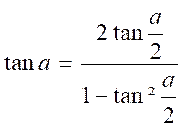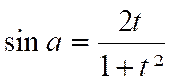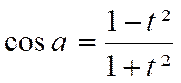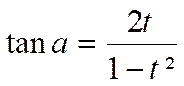Pré
requis:
|
|
|||
|
|
|
||
|
|
|||
|
|
|||
|
|
|||
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Objectif suivant : |
Retour à la liste des objectifs
de formation A savoir : les
abréviations : « tg » et
« tan » , abréviations : lire « tangente » « cotg » et
« cotan » ,
abréviations :
lire « cotangente » |
|
|
|
|
|
|
DOSSIER : LES FONCTIONS
CIRCULAIRES : ADDITION ET MULTIPLICATIONS
DES ARCS .
COSINUS,
SINUS ET TANGENTE DE LA SOMME ET DE LA DIFFERENCE DE DEUX ARCS.
En résumé :
|
Formules : Série 1 |
|
|
|
|
|
|
Sin ( a +b) = sin a cos b + sin b cos a |
|
|
|
|
“additions” |
Cos ( a +b) =
cos a cos b – sin a sin b |
|
|
|
|
|
|
|
|
|
|
Formules : Série 2 |
|
|
|
|
|
|
sin ( a – b) = sin a cos b – sin b cos a |
|
|
|
|
“Soustraction”
|
cos ( a – b)
= cos a cos b + sin a sin b |
|
|
|
|
|
|
|
|
|
II ) SINUS , COSINUS ET TANGENTE DE L’ARC «
2 a »
En résumé :
|
Formules : Série 3 |
|
|
|
|
|
|
Sin ( a +b) = sin a cos b + sin b cos a |
Devient |
Sin 2a = 2 sina cos a |
|
|
“a” et “b” deviennent
2a |
Cos
( a +b) = cos a cos b – sin a
sin b |
Devient |
Cos 2a = cos² a – sin² a |
|
|
|
|
Devient |
|
|
Problème ; exercices ;
application (formules en
cos 2a)
En résumé :
|
Formules : Série 4 |
|
|
Série 5 |
|
|
|
Cos 2a = 2 cos²a- 1 |
Qu’on peut écrire |
1 + cos 2a = 2 cos²a |
|
|
|
|
|
|
|
|
|
Cos 2a = 1 – 2 sin²a |
|
1 – cos 2a = 2 sin²a |
|
Formules : Série 6
|
|
|
|
|
|
|
TEST |
|
COURS
I )COSINUS, SINUS ET TANGENTE DE LA SOMME ET DE LA DIFFERENCE DE DEUX ARCS.
Problème posé : Connaissant les fonctions
circulaires des arcs « a » et « b », calculer les fonctions
circulaires des arcs « a + b »
et « a – b »
Nous allons établir la formule : Cos ( a +b) = cos a cos b
– sin a sin b d’où nous en déduirons toutes les autres.
|
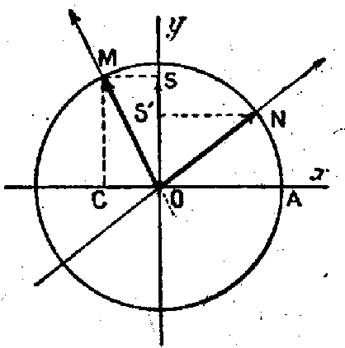
Soit le cercle trigonométrique, avec O x , axe des cosinus,et O y , axe
des sinus. A étant l’origine des arcs,marquons les extrémités M et N des arcs de mesures
respectives « a » et « b » ;. Pour introduire « a - b » ,écrivons « a – b » = l’arc AM – l’arc
AN ; = l’arc NA + l’arc AM ou d’après la formule de Chasles (info @ ) a – b =
l’arc NM à k
. 2 ou a – b = ( ON,OM) à k . 2 donc Cos ( a – b) = cos ( ON,OM) Or , le cosinus de l’angle
de deux axes est la mesure de la projection sur l’un d’eux d’un vecteur
unitaire de l’ autre ; donc : Cos ( a – b) = proj. du vecteur OM sur l’axe du vecteur ON Notons que l’on pourrait aussi bien projeter le
vecteur ON sur l’axe du vecteur OM. Les composantes du vecteur OM suivant les axes
sont : Sur O x : le vecteur OC de mesure Sur O y : le vecteur OS ,
de mesure Ce qui nous permet d’écrire que : Le vecteur OM = le vecteur OC + le vecteur OS |
|
Or, étant donné deux vecteurs OC et OS , la projection de leur résultante du vecteur OM sur un
axe a pour mesure la somme des mesures des projections des deux vecteurs ;
donc ;
La
projection
du vecteur OM (sur ON) = projection
du vecteur OC (sur ON) + projection
du vecteur OS (sur ON).
Enfin, la mesure de la projection d’un vecteur sur
un axe s’obtient en multipliant la mesure du vecteur par le cosinus de l’angle de l’axe-support
et de l’axe de projection. Donc ;
Cos
( a –b ) = ![]() cos ( Ox , ON) +
cos ( Ox , ON) +
![]() cos ( Oy , ON) ( relation 1 )
cos ( Oy , ON) ( relation 1 )
Or , d’une part ( Ox , ON ) = b
Et d’autre part , le
premier énoncé rappelé ci-dessus donne :
’ Cos ( Oy
, ON) =
projection du vecteur ON sur Oy
= ![]() = sin b
= sin b
En substituant dans le deuxième membre de ( la relation 1 ) , on trouve enfin :
Cos ( a – b) = cos
a cos b + sin a sin b
Autres formules .
Cos ( a
+ b ) .
Quels que soient les arcs « a » et
« x »x , on a :
Cos (
a – x) = (cos a) ( cos x) + (sin
a) ( sin x)
Remplaçons : “x” par “- b” :
Cos ( a – (-b) ) = (cos a) ( cos (-b) ) + (sin a) ( sin (-b) ) ; ce qui
donne :
Cos ( a +b) ) = cos a
cos (-b) + (sin a) sin (-b)
Comme : cos (-b)
= cos b , et , sin (-b)
= - sin b
Il en vient que :
Cos
( a +b) ) = cos a cos b - sin a
sin b
On dit que cette formule se déduit de la
formule cos ( a-b)
= .................en changeant “b” en (-b)
sin ( a
+ b ) .
Quels que soient les arcs « b » et
« x »x , on a :
Cos (
x -b) = (cos x) ( cos b) + (sin
x) ( sin b)
Remplaçons “x” par
“![]() -
a”
-
a”
Nous obtenons l’égalité :
Cos 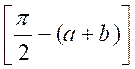 = cos (
= cos (![]() - a) cos b + sin (
- a) cos b + sin (![]() - a) sin b
- a) sin b
Or, quand deux arcs sont complémentaires, le sinus
de l’un est égal au cosinus de l’autre . Donc on peut
écrire l’égalité suivante :
Sin ( a +b) = sin a cos b
+ sin b cos a
tan ( a
+ b ) .
On a
:
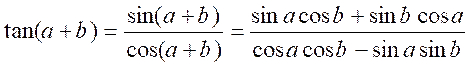
si
nous divisons en haut et en bas par « cos a cos b »
nous
obtenons :
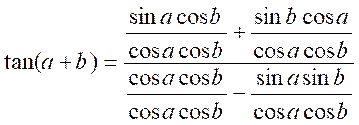
pour
enfin obtenir :
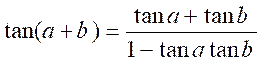
tan ( a
- b ) .
en
changeant « b » par « -b », la formule précédente
devient :
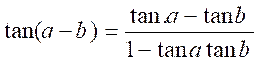
Soit en résumé les formules suivantes :
|
Formules : Série 1 |
|
|
|
|
Sin ( a +b) = sin a cos b
+ sin b cos a |
|
|
“additions” |
Cos ( a +b) = cos a cos b – sin a sin b |
|
|
|
|
|
|
Formules : Série 2 |
|
|
|
|
sin ( a - b) = sin a cos
b - sin b cos a |
|
|
“Soustraction”
|
cos ( a - b) = cos a cos b + sin a sin b |
|
|
|
|
|
Exercices :
1°) En déduire la formule qui donne tan(a-b) des formules sin(a-b) et cos (a-b)
2°)
calculer : sin 15° , cos 15° et tan 15° sachant que 15° = 60° - 45°
II) SINUS, COSINUS ET TANGENTE DE L’ARC
« 2a ».
Problème
posé : On connaît les fonctions circulaires d’un arc
« a » ; calculer les
fonctions circulaires de l’arc double « 2a »
Nous remplaçons ,
« b » par « a » dans les expressions :
Sin( a + b) , cos ( a + b) ; tan
( a +b)
On trouve : Sin( a + a) , cos
( a + a) ; tan ( a +a)
Et sin
(a +a) = sin a cos a + sin a cos
a soit : sin (2a) = 2 sina
cos a
Il en
est de même pour cos 2 a = cos cos a – sin a sin a
= cos²a – sin²a
Il en
est de même pour tan (a + a) = tan 2a
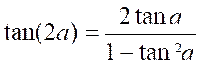
d’où en résumé , la troisième
série de formules :
|
|
Sin 2a = 2 sina cos a |
|
|
|
Cos 2a = cos² a – sin² a |
|
|
|
|
|
Exercices
résolus :
1°) On donne tan x = 2 -![]() ;
calculer « x » supposé compris entre 0 et
;
calculer « x » supposé compris entre 0 et ![]()
Calcul
de tan 2x : on trouve , après calculs tan 2x = ![]() d’ où :
(@ voir
exercice 3 , chapitre : relation entre les fonction circulaires d’un même
arc)
d’ où :
(@ voir
exercice 3 , chapitre : relation entre les fonction circulaires d’un même
arc)
Donc
2 x = ![]() ; x =
; x = ![]()
2°)
Mêmes questions pour :
a) tan y = 2 + ![]() ; même méthode : y =
; même méthode : y =![]()
b) tan
v = ![]() - 1 ;
même méthode v =
- 1 ;
même méthode v = ![]()
c) tan u
= ![]() + 1 ;
même méthode ; solution u =
+ 1 ;
même méthode ; solution u = ![]()
Application : formules en cos 2 a
Nous
écrivons
Cos 2a = cos² a – ( 1 –cos² a ) ou bien
cos 2 a = ( 1 – sin ² a ) – sin
² a
D’où
les nouvelles formules :
|
Formules : Série 4 |
|
|
Série 5 |
|
|
|
Cos 2a = 2 cos²a- 1 |
Qu’on peut écrire |
1 + cos 2a = 2 cos²a |
|
|
|
|
|
|
|
|
|
Cos 2a = 1 – 2 sin²a |
|
1 – cos 2a = 2 sin²a |
|
D’où on
tire :
|
|
|
|
Ce qui
nous permet d’énoncer le théorème suivant :
Théorème :
Sin²a , cos² a et tan ² a
s’expriment rationnellement en fonction de cos 2a . ( nota :
« rationnellement » veut dire : sans radicaux)
Activité :
Transformer en monôme 1 + sin 2a ;
1 – sin 2a (
poser 2 a = 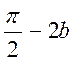 )
)
THEOREME
FONDEMMENTAL :
Les
fonctions circulaires de l’arc « a » s’expriment rationnellement en
fonction de 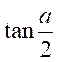
Remplaçons
« a » par ![]() dans les formules (série
3 )
dans les formules (série
3 )
|
Sin 2a = 2 sina cos a |
Devient
|
Sin a = 2 sin |
|
Cos 2a = cos² a – sin² a |
Devient |
Cos a = cos² |
|
|
Devient |
|
Cette
dernière formule donne déjà « tan a » en fonction de 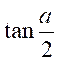 .
.
Pour
« sin a » et « cos
a » , nous observons que les seconds membres sont homogènes et du second degré en « cos
![]() »
et « sin
»
et « sin ![]() » ;
on sait que « 1 = cos²
» ;
on sait que « 1 = cos²
![]() + sin²
+ sin² ![]() » divisons
donc ces deuxièmes membres par
« 1 » puis remplaçons ;
» divisons
donc ces deuxièmes membres par
« 1 » puis remplaçons ;
Nous
obtenons :
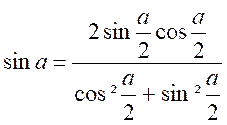 et
et 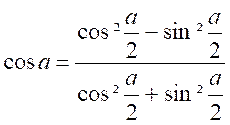
En divisant par
« cos² ![]() »,
on trouve :
»,
on trouve :
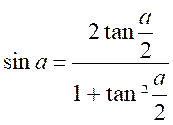 et
et 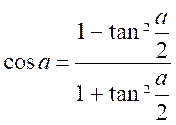
Formules : Série 6
|
|
|
|
|
|
Remarque : on a divisé par cos ![]() , cela n’est légitime
que pour : cos
, cela n’est légitime
que pour : cos ![]()
![]() ou
ou ![]()
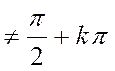 ou
ou ![]()
Si a = ![]() + k 2
+ k 2![]() , « t » est
infini , et les formules 6 donnent en divisant en haut
et en bas par « t² »
, « t » est
infini , et les formules 6 donnent en divisant en haut
et en bas par « t² »
Sin
a = 0 ; cos a = -1 ;
tan a = 0
C’est à dire les
valeurs de sin ![]() ; cos
; cos ![]() ; tan
; tan ![]()
Les formules de
la série 6 sont donc valable en toute généralité..
Reste
à refaire les exercices proposés…….
TRAVAUX AUTO _ FORMATIFS
CONTROLE:
A compléter…..