Pré requis:

Lecture : géométrie descriptive	Classe Collège 5^ème
Lecture : La représentation en Perspective	CORRIGE
A consulter : Les volumes particuliers.	Retour vers la leçon…

ENVIRONNEMENT du dossier:

Index warmaths

AVANT : 1°)Notion 2°) Au collège !!!

COURS

APRES : 1°) L’orthogonalité 2°) le parallélisme. 3°) Info ++ exercices niveau+ :

1°) Cours : plan et espace  :niveau IV 2°) Liste des cours sur la géométrie dans l’espace.

CORRIGE TITRE : Etude descriptive de l ‘espace .

Fiche 1 : Description de notre environnement.

Fiche 2 : Les droites.

Fiche 3 : Le Plan.

Fiche 4 : Droite incluse dans un plan.

Fiche 5 : Droite et plans sécants.

Fiche 6 : Droite et plans parallèles.

Fiche 7 : Position relatives d’une droite et d’un plan.

Fiche 8 : Droites coplanaires.

Fiche 9 : Droites parallèles dans l’espace.

Fiche 10 . Positions relatives de deux droites de l’espace.

Fiche 11 : Plans parallèles.

Fiche 12 : Position relatives de deux plans.

Fiche 13 : Droites perpendiculaire dans le plan.

Fiche 14 : Droites perpendiculaires dans l’espace .

Fiche 15 – Droites perpendiculaires à un plan.

Fiche 16 : Plans perpendiculaires.

Fiche 17 : Droites et plans particuliers de l’espace. (plan horizontal ; droite verticale, Plan vertical …)

Fiche 18 : exercices types ….

Travaux ; devoirs			Exo	Corrigé
TEST	Contrôle	évaluation	Et : Fiche 18 : exercices types ….	Contrôle	évaluation

Interdisciplinarités : (matière concernée)
F	H	Géo.	Vie quotidienne et vie familiale	Autres :	Sciences et technique	Physique Chimie Electricité	Statistique.

Fiche 1 : Description de notre environnement.

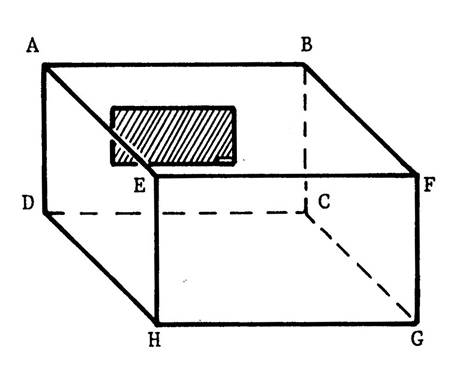
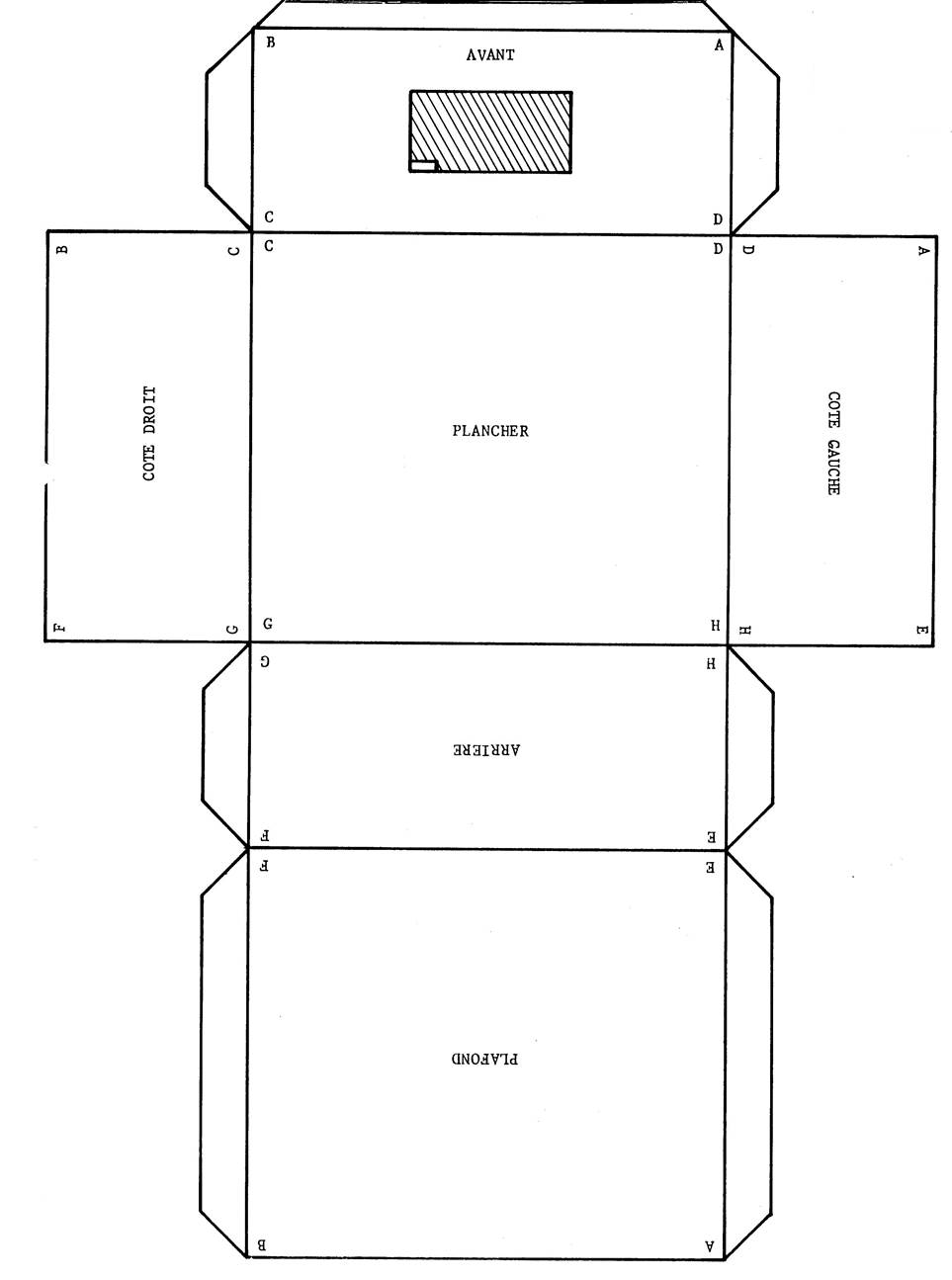
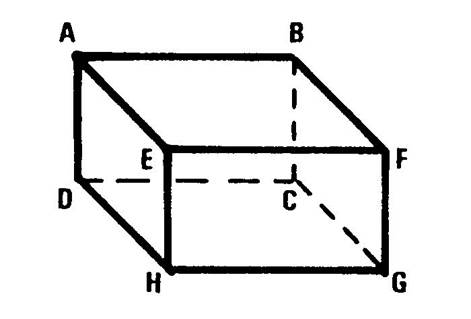
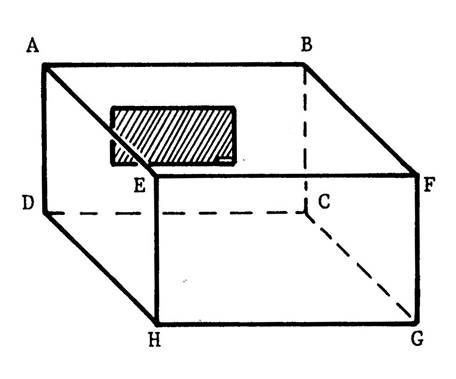
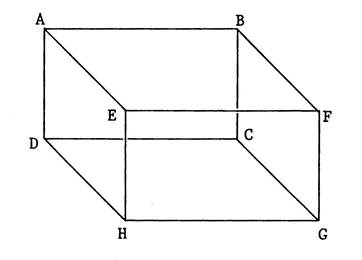
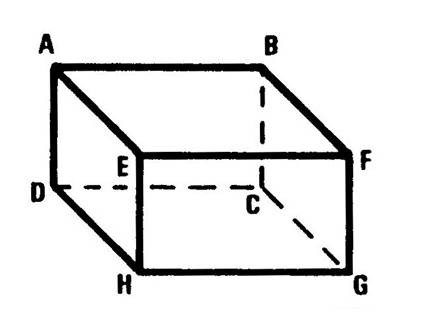
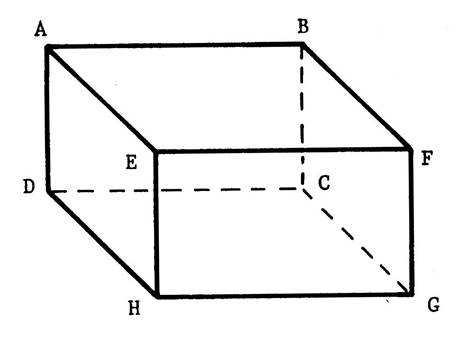
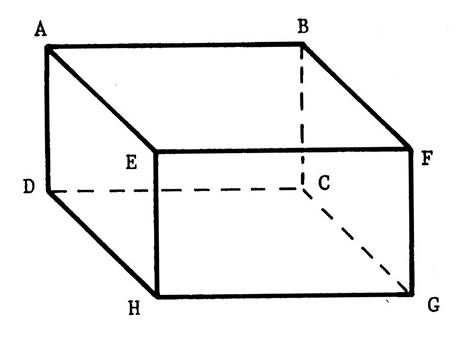
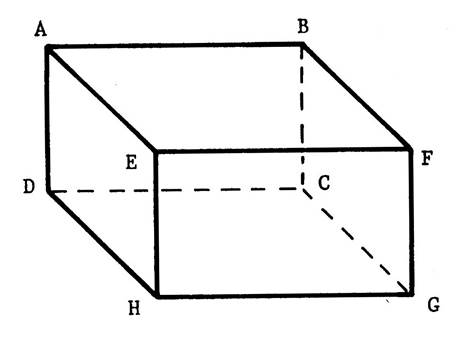
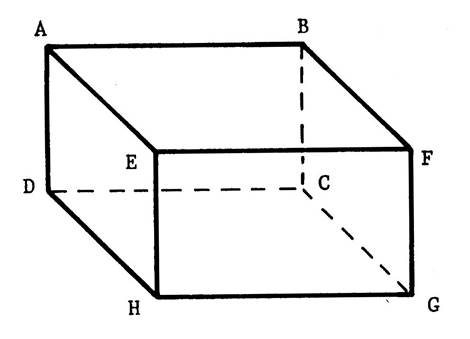
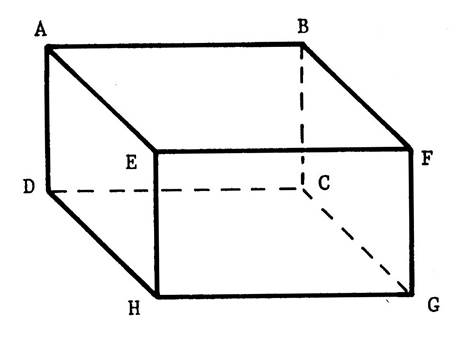
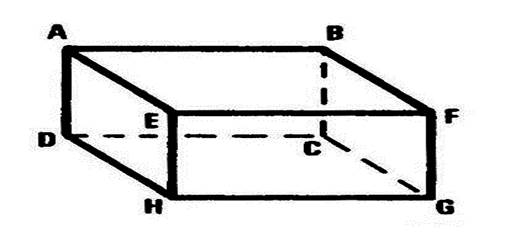
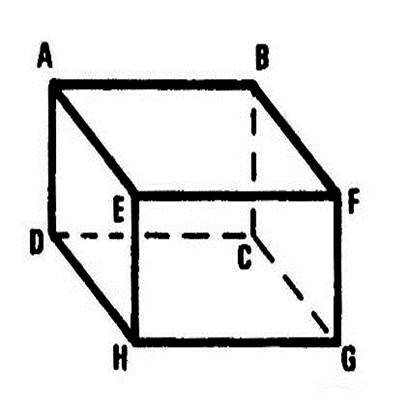
Vous êtes dans une salle ( chambre , salle à manger , salle de classe …), cette pièce peut – être considérée comme étant un parallélépipède rectangle La figure ci-contre ( salle de classe avec un tableau accroché au mur ) en est une représentation en perspective cavalière. On vous demande d’en fabriquer un modèle réduit en utilisant le patron ci-dessous. Attention : en collant les languettes , faites en sorte que les inscriptions soient apparentes.

Modèle :

Commentaires :

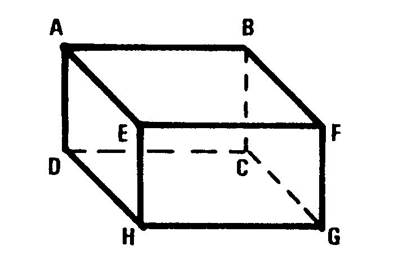
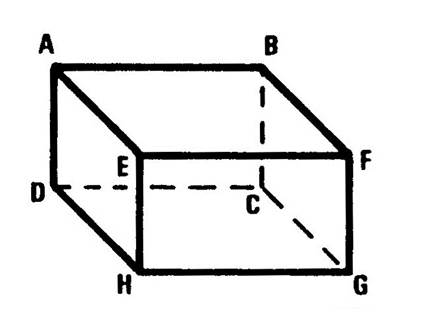
En ne tenant pas compte des imperfections, on peut considérer le plafond, le plancher, les murs comme étant des portions de « plan ». Ce sont les faces du parallélépipède rectangle. La face contenant le tableau s’appelle « ABCD ». Nommez les autres faces : ……BFGC ; EFGH ; AEHD ; ABFE ; DCGH ………………….. Combien y- en a-t-il ? …………6……….. Attention : Ne confondez pas la face et la plan la contenant : le plan est lui « illimité ».

· L’intersection du plancher et du mur contenant le tableau ( par exemple) est une portion de …. « droite »…. Nommez d’autres exemples d’intersections de faces ( préparez l’oral) Ces droites sont les arêtes du parallélépipède rectangle. Le segment [ DC ] est une arête . Nommez les autres arêtes……………….AB ; BF ; FE ; EA ; DC ; CG ; GH ; HD ; AD ; BC ; FG ; EH ; Combien y a-t-il d’arêtes ? ……12…. Attention : Ne confondez pas l ’arête et la droite la contenant : la droite est elle « illimitée ».

· Quand les arêtes se coupent , leurs intersections sont des ..points …. Ce sont les « sommets » du parallélépipède rectangle. Combien y a-t-il de sommets ? …8 …

…

Fiche 2 : Droites.

Vous savez par expérience que par deux points distincts , il ne passe qu’une seule droite.

A retenir : Deux points distincts déterminent une droite et une seule.

Question 1 : Combien y a-t-il de points dans l’espace ? …………une infinité …….. Question 2 : Combien de droites pouvez-vous imaginer ? …………une infinité ……………….

· Nous reprenons la salle de classe . ( et son modèle réduit)

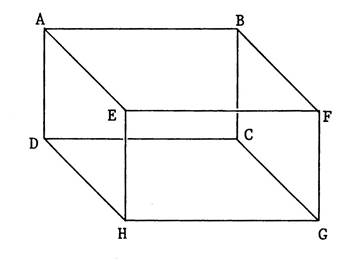
[ AB ] est une arête . ( AB ) est la droite contenant cette arête . ( A B ) est le support de [ AB ]. Activité : Nommez des droites contenant une arête . : ………………( HG ) est le support de [ HG ]. …………( BC ) ; ( CD )…………………….

· ( A F ) est une droite ne contenant pas d’arête …..

Activité : Nommez des droites qui passent par des sommets sans contenir d’arête : ………( DE )……………………………………………………………………..

Fiche 3 : Le Plan.

Info +++ le plan

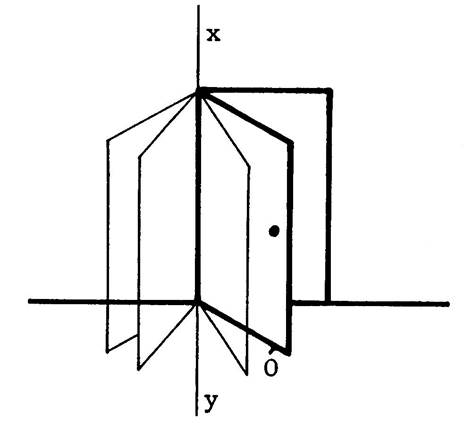
La porte de la salle de classe peut être considérée comme une portion de plan. Cette porte tourne ( pivote) autour de ses gonds. Combien de positions peut-elle occuper quand on la fait tourner autour de ses gonds ? …………….une infinité ………… Dans tous les cas , la droite « xy » est contenue dans le plan matérialisé par la porte . On dira alors :

A retenir : Etant donné une droite , il existe une infinité de plans contenant cette droite.

· Considérons un point « O » (sur le sol ). « O » n’appartenant pas à «  xy » . · Combien existe-il de positions de la porte telles que le plan de la porte passe par « O » ?...........une position ........ Cette constatation illustre une situation qui est toujours vraie.

A retenir : Une droite et un point n’appartenant pas à cette droite déterminent un plan unique.

· Vous savez que deux points distincts déterminent une droite unique. Au lieu d’une droite , il suffit donc de deux points distincts . On énoncera alors :;

A retenir : Trois points distincts non alignés déterminent un plan unique.

Remarque : Une chaise, une table à quatre pieds peuvent être bancales. (elle cogne ) Un tabouret à trois pieds ne l’est jamais . Expliquez pourquoi ? Voir , en science on parle du « le triangle de sustentation » , pour palier au problème , le quatrième pied d’un armoire doit être réglable (avec une vis )afin de faire contact avec le sol , pour éviter que l’armoire se déforme , et que les portes ne se ferment convenablement .

Nous reprenons la salle de classe et son modèle réduit. Nous allons chercher tous les plans que l’on peut désigner.

1°) Il y a déjà les plans contenant les faces. Remarque : on pourrait désigner ces plans par trois points, mais ont les désignera comme les faces elles-mêmes. Exemple : « AEHD » ; Activité : Nommez de tels plans :……

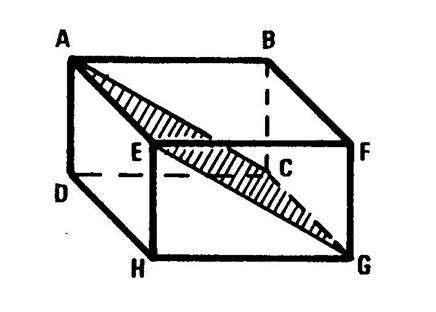
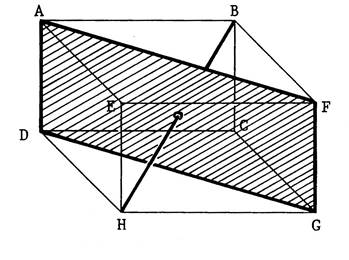
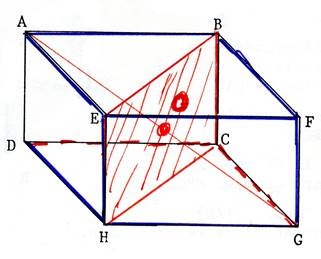
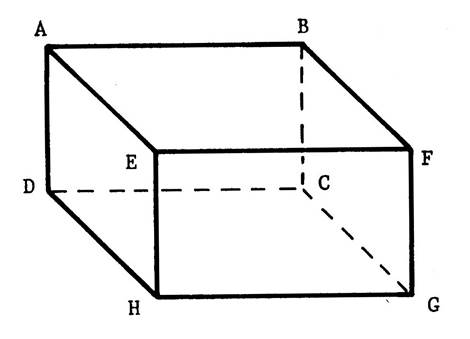
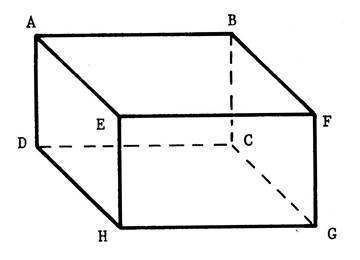
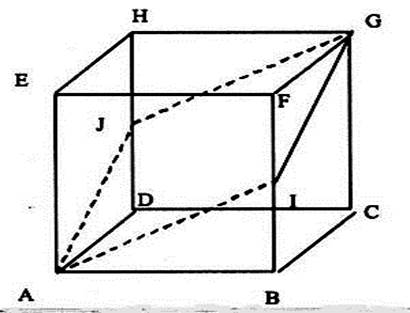
2°) Il y a des plans identifiables ne contenant pas les faces. Exemple : le plan passant par les points « ACGE » . ( ce plan est matérialisé sur la figure ci-contre par un parallélogramme hachuré). Activité : Nommez de tels plans :…  « ABGH » ; « DCFE » « DHFB »…

3°) On peut imaginer d’autres plans passant par trois points (sommets). Exemple : le plan passant par les points « E » ; « B » et « G » que l’on désignera par « E B G ». Pour vous représenter ce plan , imaginez un parallélépipède plein que l’on aurait scié suivant le plan ( de sciage) passant par les points « E » « B » « G » , Dessinez alors sur la figure ci-contre la trait de scie marqué sur les différents plans. ( le trait FG est dessiné en pointillé ) Remarque, la partie sciée est une pyramide à base triangulaire « EBG ».

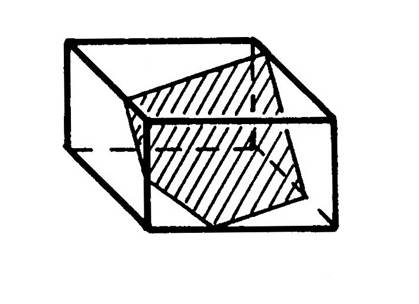
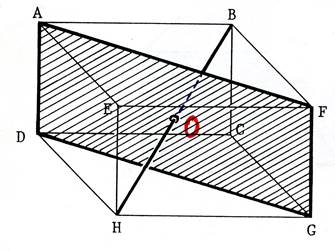
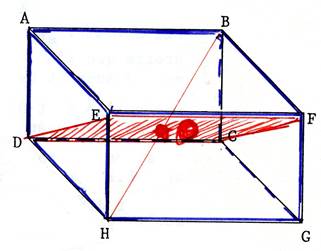
Il est possible aussi d’imaginer des plans qui ne passent pas par les sommets. Dans le dessin ci-contre nous voyons un plan qui ne passe pas par un sommet du parallélépipède rectangle.

Fiche 4 : Droite incluse dans un plan.

Info +++ : droite et plan.

Nous sommes toujours dans la salle de classe et considérons les sommets « A » et « D ». Vous savez que deux points distincts déterminent la droite que l’on appelle ( A D ) et que le support de l’arête est le segment de droite noté [ A D ]. Les points « A » et « D » sont aussi des éléments (points) du plan « ABCD ».

Tous les points (du segment) appartenant à la droite ( A D ) sont-ils des éléments du plan « ABCD » ? oui….. On peut dire ( par simplification ) que la droite ( A D ) est entièrement contenue dans le plan « ABCD » ? Il en est toujours ainsi dans des situations analogues.

A retenir : Si une droite a deux points en commun avec un plan, alors la droite est entièrement contenue dans ce plan. On dit que « la droite est incluse dans le plan » (tous les points de la droite sont alors des points du plan.)

· Nous reprenons la droite ( AD ) , elle est incluse dans le plan du tableau « ABCD ». Cette droite est aussi incluse dans un plan matérialisé par le mur, c’est le plan … «  AEHD » …… Mais elle est aussi incluse dans bien d’autres plans, il y en a un en particulier que vous pouvez nommer à l’aide des points de la vue en perspective ci- dessus , c’est le plan … «  AFGD »…..

Activité :

· La droite ( EF ) est incluse

Dans le plan …ABEF..

, dans le plan …EFGH..

,dans le plan …DCFE…

· La droite ( CG ) est incluse

Dans le plan …DCGH…..

, dans le plan …BFGC……..

,dans le plan …ACGE…

· La droite ( CH ) est incluse

Dans le plan …DCGH…..

, dans le plan ……EBCH…..

,dans le plan ……ACH……

Fiche 5 : Droite et plans sécants.

Info ++ ?

Nous considérons le plan du tableau « ABCD » et la droite ( A E ). Ils ont en commun le point « A » , en ont- ils d’autres ? …..non… La droite ( AE ) est-elle incluse dans le plan « ABCD » ? …Non…. Dans ces conditions, on dit que la droite ( AE ) est sécante au plan « ABCD » en « A » On encore on peut écrire : que la droite ( AE ) coupe le plan « ABCD » en « A ». · « A » est appelé le point d’intersection de la droite ( A E ) et du plan « ABCD »

· De même , la droite ( C F ) et le plan « ABCD » n’on en commun que le point «  C » On peut dire alors que la droite ( CF ) coupe le plan « ABCD » en « C ». Ou encore on peut dire que la droite ( CF ) est sécante en « C ».

A retenir : « Une droite est sécante à un plan » ( ou «  une droite coupe un plan »)signifie que : La droite et le plan ont en commun un point unique.

Remarque : On dit aussi que le plan coupe la droite ou que la droite et le plan sont sécants.

· Nommez des droites sécantes au plan «  ABFE » : ……( A D ) ; ( BC ) ; ( FG ) ; ( EH ) ;….... · Nommez des plans coupés par la droite ( HG ) : ……… «  AEHD » ; « BFGC »………………..

Activité : Représenter l’intersection d’une droite et d’un plan.

Ci- dessous , le dessin montre l’intersection du plan « ADGF » et la droite ( BH )

Ci- dessous , le dessin repris ci-contre et montre l’intersection du plan « ADGF » et la droite ( BH ), ligne en pointillée sert à assurer la continuité du segment BH . (partie cachée du segment par le plan hachuré « AFGD »

On a représenté en traits fin (esquisses) deux dessins de la salle de classe. ( en prenant exemple ci-dessus)

Figure 1 : En ne repassant en traits forts que ce qui est nécessaire , vous allez mettre en évidence l’intersection du plan « EBCH » et la droite ( AG ) .

Figure 2 : En ne repassant en traits forts que ce qui est nécessaire, vous allez mettre en évidence l’intersection du plan « CDEF » et la droite ( BH ) .

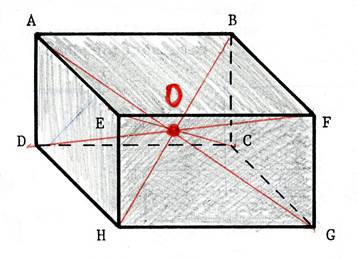
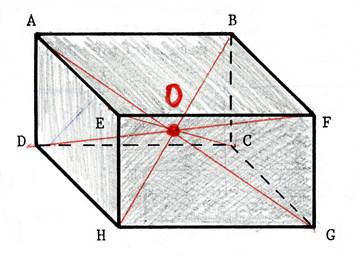
L’intersection des diagonales se coupent en un point appelé : centre de gravité du parallélépipède rectangle.

Fiche 6 : Droite et plans parallèles.

Info +le parallélisme en géométrie dans l’espace+ ?

Nous considérons le plan « ABCD » et la droite ( FG ). Remarque : il faut penser que le plan n’est pas limité à la face « ABCD » et que la droite ( FG) n’est pas limitée à l’arête du segment noté [FG] ; Question : la droite et le plan ont-ils un point commun ? …NON …. On dit alors que la droite ( FG ) est parallèle au plan « ABCD »

A retenir : Si une droite n’a pas de point commun avec un plan , on dit qu’elle est parallèle à ce plan ou que le plan est parallèle à la droite.

Activités :

1. Nommez des droites parallèles au plan « ABCD »

( EF ) ; ( F G ) ;  ( G H ) ; ( H E )

2. Nommez des droites parallèles au plan « DCGH »

( AB ) ; ( BF ) ; ( FE ) ; ( E A )

3. Nommez des droites parallèles au plan « EBCH »

( AD ) ; ( F G )

4. Nommez des plans parallèles à la droite « AE »

«  ABFEF » ; «  BFGC » ; « DCGH » ; « AEHD »

Fiche 7 : Positions relatives d’une droite et d’un plan.

Info ++ position d’une …..

La position d’une droite par rapport à un plan sera fonction du nombre de points communs.

Nombre de points communs

Position relative de la droite et du plan.

« 0 »

La droite et le plan sont parallèles

« 1 » (exactement)

La droite et le plan sont sécants.

« 2 » ( au moins (minimum) 2 )

La droite est incluse ( confondue) dans le plan.

Voir :aussi parallèle.

Ci-dessous représentations graphiques des cas précédents.

Droite et plan parallèle

Droite et plan sécants

Droite incluse (confondue) dans le plan.

A retenir : Une droite et un plan sont parallèles signifie que : La droite et le plan n’ont pas de point commun, ou que, la droite est incluse (confondue) dans le plan.

Si on veut préciser que la droite n’est pas incluse dans le plan, on dit : « La droite et le plan sont strictement parallèles ».

Fiche 8 : Droites coplanaires.

« Droites coplanaires » signifies « droites incluses dans un même plan » .

Exemple : Voir la figure ci-contre : ( A B ) ; ( AD) ; ( D B ) ; ( CD ) sont des droites coplanaires car elles sont toutes incluses dans le plan ….  « ABCD ».. Au vu de ce qui est dit précédemment, dites, en expliquant si ( EC) et ( HB ) sont coplanaires. .Oui , car elles sont incluses dans le plan « EBCH ».

Activités :

· Expliquez ( à préparer pour l’oral) pourquoi ( AD ) et ( HG ) ne sont pas coplanaires. ( AD) appartient au plan « ABCD » , (HG) appartient au plan « EFGH » , le plan « ABCD » et « EFGH » sont strictement parallèles , donc les droites qu’ils contiennent sont parallèles et donc non coplanaires.

· ( AB) et ( FG ) sont-elles coplanaires ?.............non....................... · ( BC ) et ( DG ) sont-elles coplanaires ? ………non……………. · Nommez des droites non coplanaires : …………( FG ) et ( DC )……à vous d’en trouver d’autres !!!….

Positions relatives de deux droites coplanaires .

· Deux droites d’un plan qui ont en commun deux points sont « confondues  » Dans ces conditions, elles ont alors tous leurs points communs.

· Deux droites d’un plan qui ont un seul point commun sont dites «  sécantes »… Nommez de telles droites de la salle…….(EH) et (HG)

· Deux droites d’un plan qui n’ont pas de point commun sont appelées « droites parallèles » Trouvez dans le plan «  AEHD » de telles droites : …………( AD) et ( EH) ; ( AE ) et ( DH)………………

Remarque Dans le plan « droites parallèles » signifie que se sont des droites qui n’ont pas de points commun ou qui sont confondues.

Fiche 9 : Droites parallèles dans l’espace.

Dans l’espace pour que deux droites soient parallèles, il faut qu’elles soient coplanaires.

A retenir : Dans l’ensemble des droites de l’espace : «la droite  « d » et la droite « d’ » sont parallèles signifie que « d » et « d’ » sont coplanaires et sans point commun ou qu’elles sont confondues.

«la droite  « d » et la droite « d’ » sont parallèles se dit aussi « d » et « d’ » ont même : …support……..

Activité : ( AD ) est-elle parallèle à ( FG) ? …oui .. ( AF ) est-elle parallèle à ( DG) ? …oui … Nommez des droites parallèles qui ne sont pas le support d’arêtes. ( HC) et (EB) ; ( BD ) et (FH ), ( AH ) et (BG) ; …( EG ) et ( AC)

Fiche 10 . Positions relatives de deux droites de l’espace..

Nombre de points communs

Position relative de deux droites .

« 0 »

Les droites ne sont pas coplanaires Ou Les droites sont strictement parallèles et alors elles sont ……………………..

« 1 » (exactement)

Les droites sont ..sécantes… et alors elles sont

« 2 » ( au moins « 2 »)

Les droites sont …… confondues…

Fiche 11 : Plans parallèles.

Ci-contre on vous a dessiné un solide en perspective. Les faces «  ABCD » et « EFGH » ont-elles un point commun ? …Non... Dans le cas d’un parallélépipède rectangle parfait, le plan « ABCD » et le plan « EFGH » n’ont pas de point commun. On dit alors que le plan « ABCD » et le plan « EFGH » sont parallèles.

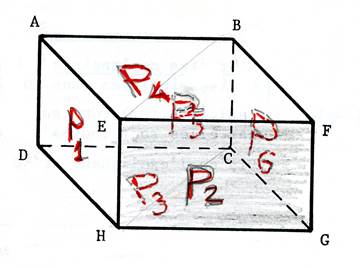
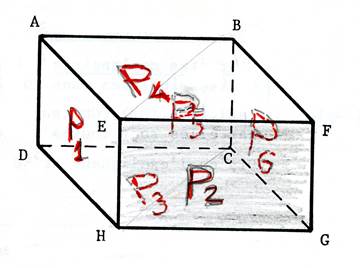
Activité : nommez les plans parallèles de la salle ( on appelle chaque plan par la lettre « P »

A scanner

A retenir : Un plan « P » et un plan « P’ » sont parallèles signifie que : « P » et « P’ » n’ont pas de point commun ou sont confondus. ( Les points de l’un appartiennent à l’autre.)

Dans ce cas , on dit que les plans ont même direction.

Fiche 12 : Positions relatives de deux plans.

Info +++

Considérons deux plans , trois cas peuvent se produire

1°) Les deux plans ont en commun trois points distincts non aligné. Vous savez que trois points distincts non alignés déterminent un plan unique, donc les deux plans sont ……confondus… 2°) Les deux plans n’ont pas de point commun . On dit alors qu’ils sont strictement parallèles. 3°) Les deux plans ont un point commun. Vous prouverez dans un niveau d’étude supérieur qu’ils ont alors une droite commune. On dit que ces plans sont sécants ( ou qu’ils se coupent ) Ils se coupent suivant une droite appelée « droite d’intersection.

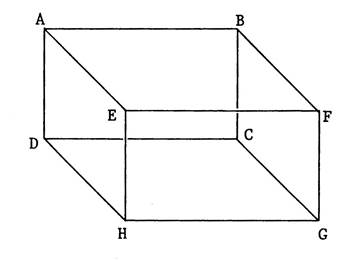
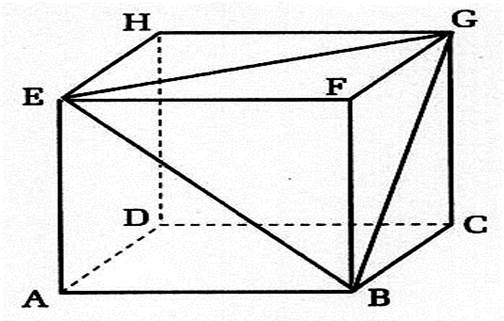
Activités : Considérons le dessin de la classe ci-contre. Les plans «  ABFE » et « DABC » se coupent suivant la droite : « AB » Les plans «  AEGC » et « DHEA » se coupent suivant la droite : « AE » Les plans «  DCGH » et « AFGD » se coupent suivant la droite : « DG » Les plans «  EHCB » et « DBFH »’ se coupent suivant la droite : « BH »

Ci-dessous représentation graphique des plans parallèles et sécants.

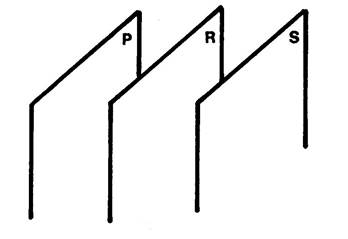
Plans parallèles :

Plans verticaux

Plans horizontaux.

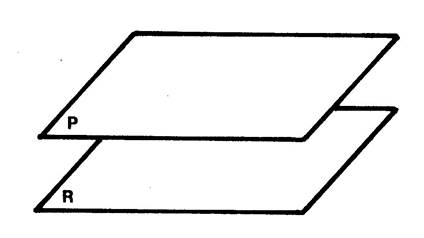
Plans sécants :

Droite d’intersection verticale.

Droite d’intersection horizontale.

Fiche 13 : Droites perpendiculaire dans le plan.

Info ++

Rappel 1 : vous avez vu précédemment …Et cette année ..

A retenir : « d » et d’ » étant deux droites d’un plan , « d » et « d’ » sont perpendiculaires signifie que : l’un des angles déterminés par « d » et « d’ » est un droite .

« d » et « d’ » sont perpendiculaires peut s’écrier «  d d’  ».

Remarque : si « d » et « d’ » sont perpendiculaires, non seulement « d » et d’ » déterminent un angle droite, mais elles en déterminent d’autres . Combien en tout ? ………….une infinité…….

· La salle de classe est un parallélépipède rectangle, que pouvez-vous dire des faces quant à leur forme ? ….ce sont des rectangles … · Dans le plan « ABFE » , trouvez des droites perpendiculaires  remarquables : « AD » ; »BC » ; « FG » ; « EH ».

Fiche 14 : Droites perpendiculaires dans l’espace .

Info +++( attention : « direction » et « sens »ne pas confondre …)

Reprenons l’exemple de la salle de classe . Les droites : ( AB) ; ( EF ) et ( HG) sont parallèles , elles ont même « direction » ; · La droite ( AD ) est perpendiculaire à la droite ( AB). · ( EF) ayant même direction que ( AB) on dit aussi que ( AD) est perpendiculaire à ( EF) . · De même ( AD ) est perpendiculaire à ……( HG ) ….

Si « d » est perpendiculaire à « d’ » , on dit alors que : « d » est perpendiculaire à toutes les droites qui ont la même direction que « d’ » . ( que ces droites coupent ou non la droite « d »)

A retenir : Dans l’espace , deux droites perpendiculaires signifie que ces droites sont respectivement parallèles à deux droites d’un plan qui sont-elles –mêmes perpendiculaires.

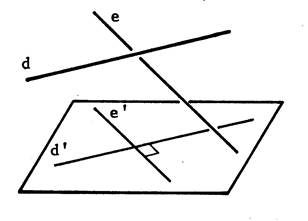
Exemple : Voir ci-contre : · On vous dit que : « d » et « e » ne sont pas sécantes. · Pourtant « d » et « e » sont perpendiculaires, car «  d // d’ » et « e // e’ » et «  d’ e’ »

Activité :

Nommez des droites de la salle de classe qui sont supports d’arêtes et qui sont perpendiculaires sans être coplanaires : ……..( EF) et (AD) ;( AE ) et ( HG) ; ….. · Que pouvez-vous dire du polygone «  DBFH » quant à sa forme ?......c’est un rectangle………. · Complétez : ( DB) .…( BF) ; ( BF) …//..( DH) ; ( BF) ….( FH ) ; ( DB ) .//…( FH) · Nommez des droites de la salle qui ne sont pas supports d’arêtes et qui sont perpendiculaires à ( BC). …………………………( EB ) ; ( HC ) ……………………………………….

Fiche 15 – Droites perpendiculaires à un plan.

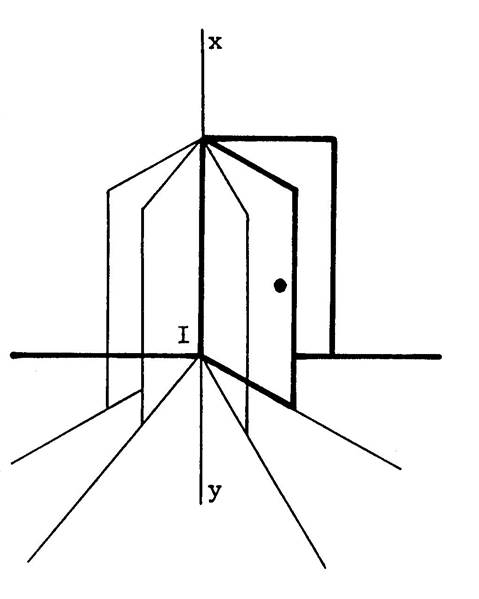
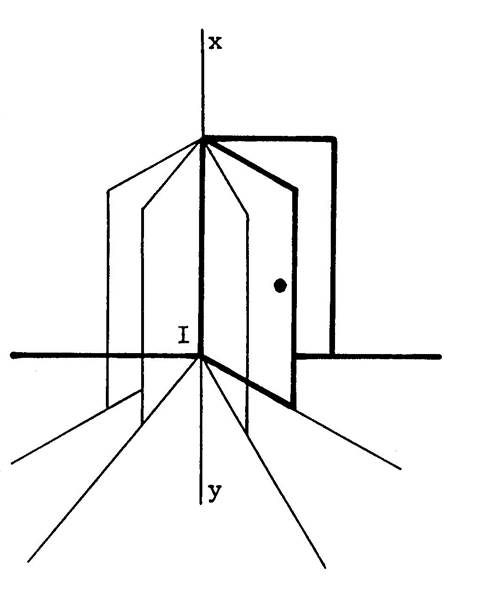
Considérons une porte (celle de la classe) tournant autour de ses gonds et ( xy) est la droite passant par les gongs et « I » l’intersection de ( xy ) avec le plan du sol. Que pouvez-vous dire de la porte quant à sa forme ? c’est un rectangle. Donc le bas de la porte est ….perpendiculaire …..à « (xy). La droite définie par le bas de la porte peut être considérée comme une droite du plan du sol. Donc la droite ( xy) est perpendiculaire à toutes les droites du plan du sol qui passe par « I » . ( xy ) est également perpendiculaire à toutes les droites du plan qui sont parallèles aux droites précédemment nommées. Donc ( x y ) est perpendiculaire à toutes les droites du plan du sol. Dans ces conditions, on dit que ( xy ) est perpendiculaire au plan du sol.

A retenir : Dire qu’une droite est perpendiculaire à un plan c’est dire qu’elle est perpendiculaire à toutes les droites de ce plan.

Remarque : Au lieu de dire « la droite est perpendiculaire au plan » , on dit aussi : « le plan est perpendiculaire à la droite » ou «  la droite et le plan sont perpendiculaires ».

Activité :

Trouvez sur la figure ci-contre ( salle de classe) · Des droites perpendiculaires au plan « ABCD » : …………(AE) ;( BF) ;(CG) ; (DH)……………….. · Des plans perpendiculaires à la droite ( BC ) ………  « ABCD » ; « BFGC  »……………………………… · Des exemples de droites et de plans perpendiculaires. ………………(EH) et « AEHD » et « EFGH »…………

Fiche 16 : Plans perpendiculaires.

Nous reprenons l’exemple de la porte tournant autour de ses gonds. Le plan de la porte contient la droite ( xy ). La droite ( x y ) est perpendiculaire au plan du sol. Dans ces conditions, on dit que le plan de la porte est perpendiculaire au plan du sol.

A retenir : «  Un plan « P » est perpendiculaire à un plan « P’ » signifie : « P » contient une droite perpendiculaire à « P’ ».

Remarque : On démontre que si « P » est perpendiculaire à « P’ » signifie que «  P » contient une droite perpendiculaire à « P’ », on peut dire alors que « P » et « P’ » sont perpendiculaires.

Activité :

On vous demande de trouver dans la figure de la salle de classe : · Des plans contenant des faces et qui sont perpendiculaires à « ABFE » : « ABCD » ; « BFGC » ; « EFGH » ; « AEHD » . · Des plans ne contenant pas de face et qui sont perpendiculaires à « DCGH ». : «AFGD » et « EBCH » . · Des plans perpendiculaires à «  ACGE » : « ABCD » et « EHGH » · « 6 » plans perpendiculaires à « BCGF » : « ABCD » ; « ABFE » ; « EFGH » ; « DCGH » ; « DEFC » ;  « ABGH »

Fiche 17 : Droites et plans particuliers de l’espace.

Plan horizontal : Le sol, le plafond sont des portions de plan horizontal. De même, la surface d’un lac quand l’eau est calme peut être considérée comme étant un plan horizontal . Préparation d’un oral : Donnez d’autres exemples.

Droite horizontale.

« horizontale et verticale »

Toute droite incluse dans un plan horizontal est appelé « droite horizontale ». Préparation d’un oral : Donnez des exemples de droites horizontales. Dans la pratique, pour vérifier qu’une droite est horizontale, on utilise un niveau à bulle.

Droite verticale .

« horizontale et verticale »

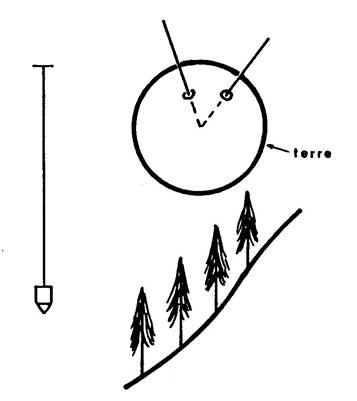
Une droite verticale est une droite dont la direction est celle indiquée par le « fil à plomb ». · En un point de la terre, la verticale est la droite passant par ce point et le centre de la terre. Dans une petite région de la terre, on admet que les verticales sont parallèles. Mais une verticale à Paris n’est pas parallèle à une verticale à Caracas.

Exemples de verticales : - Des poteaux électriques - Les sapins poussent toujours verticalement, même si le sol est en pente. - Préparation d’un oral : trouvez d’autres exemples…

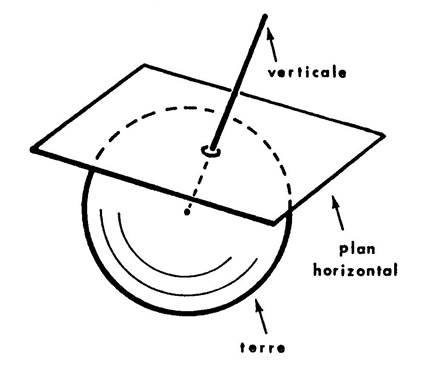
Info : sphère terrestre

Voir ci-contre le dessin : · En un point de la terre, le plan horizontal et la verticale passant par ce point sont perpendiculaires. · La terre étant considérée comme une sphère , on dit que le plan horizontal en un point est tangent à la sphère en ce point. · Dans une petite région de la terre, que pouvez-vous dire d’une droite horizontale et d’une droite verticale l’une par rapport à l’autre ?.... elles sont perpendiculaires.

Plan vertical.

Un plan vertical est un plan contenant une droite verticale. Exemple ; en général, les murs des maisons sont verticaux. Préparation d’un oral : Donnez des exemples de plans verticaux.

· Dans une petite région de la terre , que pouvez-vous dire d’un plan horizontal et d’un plan vertical l’un par rapport à l’autre ?.....ils sont perpendiculaires…

Activité :

Reprenons le dessin de la salle de classe. A l’aide des points de cette figure, nommez : - Des plans horizontaux : … « DCGH » ; « ABFE »……... - « 12 » droites horizontales :…(AB) ;(BF) ;(FE) ;(EA) ;(AF) ; (BE) ;(DG) ; ( CH) ; (DC) (CG ) ( GH) ( HD) - Des droites verticales ……(AD) (BC) (FG ) (EH)…… - « 6 » plans verticaux :… « AEHD » ,  « AFGD » ; « EBCH » ; »ABCD » ; « BFGC » , « EFGH » ……….

Cliquez ici : Fiche 18 : voir les exercices types ….

Voir le cours .

CONTROLE:

EVALUATION:

Discuter sur la position des droites  :