|
Niveau V |
Niveau : Classe 4ème |
Pré requis:
|
|
|
|
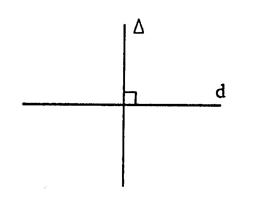
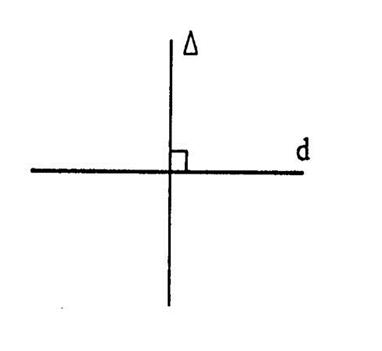
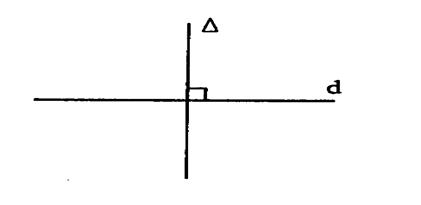
Tracé d’une perpendiculaire à une droite |
|
ENVIRONNEMENT du dossier:
|
|
|
|
|
|
Objectif précédent 1°) les
projections orthogonales 2°) L’isométrie et la rotation axiale et la
symétrie axiale. |
Objectif suivant
1°) Vers les
généralités sur les symétries. |
DOSSIER « LES SYMETRIES »
Fiche d’activités sur la SYMETRIE ORTHOGONALE .
(dit aussi : symétrie axiale )
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Devoir
Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé évaluation |
|
|
|
|
|
||
|
|
Définition : « M »
et « M ’ » étant deux points distincts et « La droite « |
|
|
||
|
|
Tout point de l’axe de symétrie est son propre
symétrique et tout point qui est son propre symétrique est situé sur l’axe de
symétrie. |
|
|||
|
|
Vous
avez vu en 6ème que : Dans toute symétrie par
rapport à une droite , si deux figures sont
symétriques , alors elles sont …superposables….. En
particulier, l’image d’une droite est une ……droite
… |
|
|||
|
|
|
|
|||
|
|
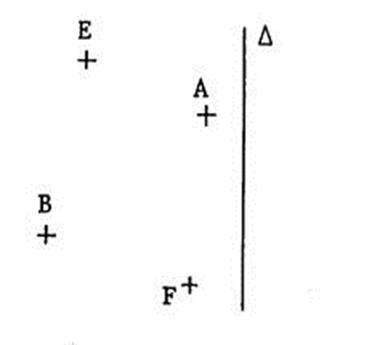
Activité
n° 1… Dessinez
en rouge l’image « |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Activité
n° 2… |
|
|||
|
|
Dessinez les images
« A’ », « B’ », « C’ » et
« F’ » des points de « A » ; « B » , « C » et « F » dans la symétrie
orthogonale d’axe « (AB) et (EF) se coupent en
« H ». (A’B’) et (E’F’) se coupent en
« H’ ». Démontrez que « H’ » est
le symétrique de « H ». |
|
|
||
|
|
Réponse : Dans la
symétrie orthogonale d’axe « La droite ( AB ) à onc pour
symétrique la droite « ( A ‘ B ‘ )de même
( EF ) a pour symétrique ( E’ F ‘ ) . Le
point « H » est situé a la fois sur la droite
( A B ) et la droite ( E F)
son symétrique est donc situé
sur la droite ( A’ B’ ) et la droite
( E’ F’) Or les droites ( A’ B ‘ )
et ( E’ F’ ) ont un seul point commun : c’est le point « H’ » donc
« H’ » est le symétrique de « H » dans la symétrie
orthogonale d’axe « |
|
|||
|
|
|
|
|||
|
|
Activité
n° 3… |
|
|||
|
|
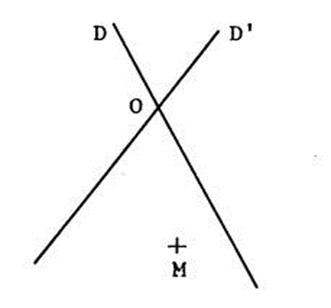
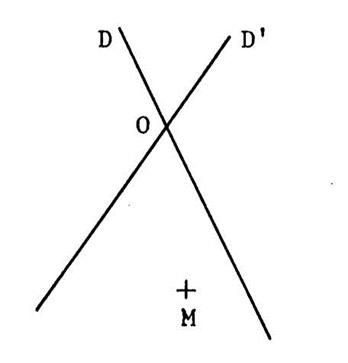
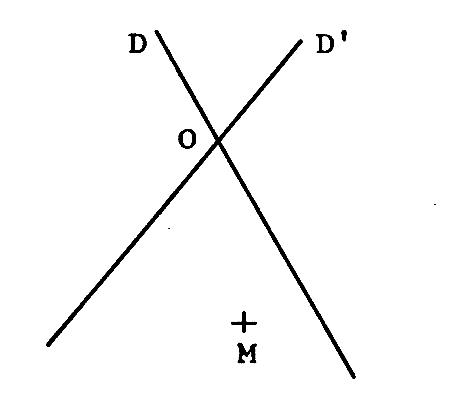
Deux droites « D » et « D’ »
se coupe en « O » . « M »
est un point situé sur « D » et « D’ ». « N » est le symétrique de « M » par rapport à « D ». « P » est le symétrique de « M » par rapport à « D’ ». 1°) Démontrez que « ON = OP » 2°) ( MN ) coupe « D »
en « H » et ( MP )
coupe « D’ » en « K ». Démontrez que ( HK ) est
parallèle à ( NP ). |
|
|
||
|
|
|
|
|||
|
|
Activité
n° 4… |
|
|||
|
|
On donne quatre points de « A » ;
« B » , « C » et « D »
tels que [AB] et [CD] aient la même médiatrice « d ». 1°)
Démontrez que « AC = BD »
et « AD = BC ». 2°)
( AC ) et (BD ) se coupent en « I » . (AD ) et ( BC ) se coupent en « J ». Démontrez
que « I » et « J »
sont situé sur « d ». |
|
|
||
|
|
|
|
|||
CONTROLE
1°) Que conserve une symétrie orthogonale
conserve ?:
Série1 :
|
Tracer la symétrie orthogonale |
|
|
|
|
|
|
|
- d’un segment de droite. |
|
|
|
-d’une droite. |
|
|
|
- d’un angle |
|
|
|
Tracer la symétrie orthogonale d’une figure
géométrique simple. |
|
|
|
|
|
|
|
Cercle |
|
|
|
Disque |
|
|
|
triangle |
|
|
|
Carré |
|
|
|
Rectangle |
|
|
Série 2 :
Construction
de l’image d’une figure :
En utilisant le quadrillage , dans chacun des deux cas ,
dessiner les images des figures ci-dessous dans la symétrie orthogonale d’axe
« d »
|
1°)
|
|
2°)
|
3°) Dessiner la figure ci-dessous
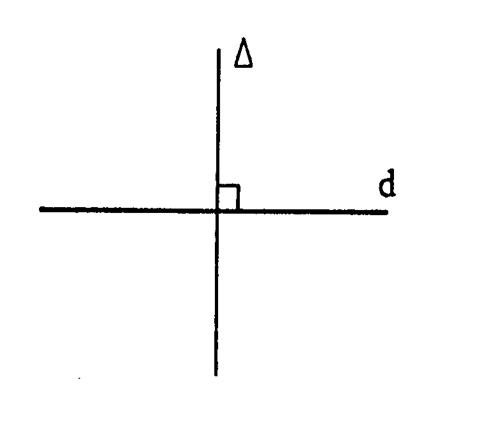
dans la symétrie orthogonale d’axe « delta » . Pour cela il faut déterminer l’image de certains points .
Laisser les droites
perpendiculaires à « delta » apparentes
|
|
4° )COMPOSITION de deux
symétries orthogonales d’axes perpendiculaires.
xx’ et yy’ sont deux
droites perpendiculaires sécantes en « O ».Dessiner l’image F’ de la
figure « F » dans la symétrie
orthogonale d’axe x’x
puis l’image « F’’ » de la figure « F’ » dans la
symétrie orthogonale d’axe yy’ .
|
|
