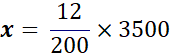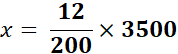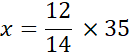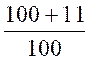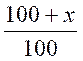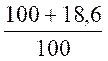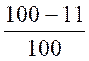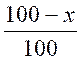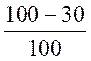|
|
|
|
|
|
Leçon : le résumé sur les %
|
Corrigé ici
|
Pré requis : calculs à savoir faire avant de
travailler les pourcentages
Faire les
calculs suivants : (en relation avec les pourcentages)
|
Multiplication
d'une fraction par un nombre : |
||
|
|
|
|
|
|
|
|
|
2,45 = |
|
|
|
Algèbre : rechercher la valeur de "x" ( SOS
Cours :Calcul nécessitant une
ou des transformations J |
||
|
245 = |
|
|
|
168 = |
|
|
|
Soit
l’égalité de la forme : |
|
|
|
Calculez : |
|
|
|
|
|
|
|
694,4 = ( |
|
|
|
1126,7 = ( |
|
x = |
|
Soit l’égalité
de la forme : |
y = ( |
|
|
Calculez : |
|
|
|
x = ( |
|
x = |
|
486,75 = ( |
|
x = |
|
626,5= ( |
|
x = |
Pré requis 2
|
Calculs : Fractions
équivalentes (égalité de deux fractions) |
|
|
Multiplication de deux
fractions |
|
|
Multiplication d'une
fraction par un nombre |
|
|
Algèbre : résoudre
une équation du premier degré à une inconnue |
|
|
A propos de
"a%" |
|
tableau |
DOSSIER: Résumé sur les opérations avec les POURCENTAGES
|
|
I )
Calcul du pourcentage d’un nombre
( a% = ![]() )
)
y
= ![]() x
; ou y =
x
; ou y = 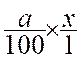 =
= 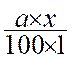 =
= ![]()
ou
« y » est la valeur de l’augmentation ou diminution
« a »
la valeur du taux
« x » le nombre sur lequel
s’applique le taux.
Exemple : on veut calculer 8% de 120
On
transforme : 8% = ![]()
On
calcule : ![]() ´ 120
=
´ 120
= 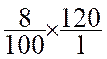 =
= 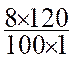 =
= 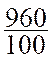 = 9,6
= 9,6
Conclusion : 8% de 120 = 9,6
II )
Calcul d’une « diminution » ou « augmentation »: Pour calculer la
valeur de l’augmentation au la valeur
d’une diminution d’un prix (ou autre grandeur) préalablement exprimée en pourcentage
,on appliquera la relation :
|
SOS COURS ! ! ! calcul d’un
pourcentage d’un nombre |
Possibilités
de calculs
Calcul
direct :
Si l’on connaît la valeur de « x »
et « a » on peut calculer « y ».
Calcul par
transformation :
Si l’on
connaît la valeur de « y » et « a » on peut calculer
« x ».
Si l’on
connaît la valeur de « y» et « x» on peut calculer « a».
III) Calcul
d’un nouveau prix ou grandeur après une augmentation :
Y
= (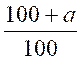 ) x
) x
ou
« y » est le nouveau prix
ou grandeur recherché
« a »
est le taux de l’augmentation
« x » est le prix ou le
grandeur sur lequel s’exerce le taux d’augmentation .
|
SOS COURS : calcul après une
augmentation et vis versa |
Possibilités
de calculs
Calcul direct :
Si l’on connaît la valeur de « x »
et « a » on peut calculer « y ».
Calcul par
transformation :
Si l’on
connaît la valeur de « y » et « a » on peut calculer
« x ».
Si l’on
connaît la valeur de « y» et « x» on peut calculer « a».
II ) Calcul d’un nouveau prix ou
grandeur après une
diminution :
Y = (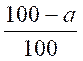 ) x
) x
ou
« y » est le nouveau prix
ou grandeur recherché
« a »
est le taux de la diminution
« x » est le prix ou le
grandeur sur lequel s’exerce le taux de diminution .*
|
SOS COURS : calcul après une
diminution et vis versa |
Possibilités
de calculs
Calcul
direct :
Si l’on connaît la valeur de « x »
et « a » on peut calculer « y ».
Calcul par
transformation :
Si l’on
connaît la valeur de « y » et « a » on peut calculer
« x ».
Si l’on
connaît la valeur de « y» et « x» on peut calculer « a».
PROCEDURE
DE RESOLUTION à appliquer à chaque cas
.une fois l’énoncé donné
1°) Identifier la relation mathématique à
appliquer :
se
poser la question : dans
quel cas suis je ?
y
= ![]() x ou Y = (
x ou Y = (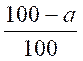 ) ou Y = (
) ou Y = (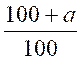 ) x
) x
2°) Identifier , dans
l’énoncé :
« y »= ; « x » = ; « a » = ;
3°) ensuite , Remplacer dans la relation mathématique les
valeurs identifiées précédemment.
4°) (il reste une inconnue) faire les
transformations, et les calculs
5°) Rendre compte (après avoir vérifié) .