Informations
pédagogiques sur Les transformations
possibles :
|
|
Equation
|
Graphe
|
Tableau
|
Représentation graphique
|
A partir
d’une Equation on peut obtenir :
|
|
x
|
x
|
x
|
A partir
d’une Graphe on peut obtenir :
|
x
|
|
x
|
x
|
A
partir d’une Tableau on peut
obtenir :
|
x
|
x
|
|
x
|
A partir
d’une Représentation graphique on peut obtenir :
|
x
|
x
|
x
|
|
|
DOSSIER :
FONCTIONS
LINEAIRES / Objectif cours 43 |
Pré requis
|
|
|
|
|
|
|
Fonction
"généralités" |
|
|
Les
Grandeurs proportionnelles |
ENVIRONNEMENT
du dossier
|
Objectif précédent : |
DOSSIER
LA FONCTION
LINEAIRE et
Son TABLEAU DE PROPORTIONNALITE
1°) On peut obtenir un tableau de
proportionnalité à partir d’ un graphe
2°) On peut obtenir
un tableau de
proportionnalité à partir d’une équation.
3° ) On peut obtenir un tableau de proportionnalité à
partir d’une représentation graphique
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Liste de situations problèmes en lien avec la fonction
linéaire. |
|
|
|
TABLEAU de (variation) dit « tableau de proportionnalité »
(regroupant les couples ( x ; ax) )
Remarque :
Un tableau
numérique représente une fonction linéaire si les couples de nombres
sont proportionnels .
Sinon , le tableau ne représente pas une fonction linéaire
.
On peut obtenir un tableau de proportionnalité à partir d’ un graphe: d’une équation ;; d’une représentation
graphique.
Voir Fonction généralité « le le
tableau de
variation »@ :
1°) On peut obtenir un tableau
de proportionnalité à partir d’ un graphe
Soit le graphe :
G = { ( -3 ; -9) ; (-2 ;-6 ) ; (-1 ;-3
) ; ( 0 ; 0 ) ; (1 ;
3 ) ; (2 ;6 ) ; ( 3 ;9 ) ; .........
}
On place les couples de nombres dans le tableau suivant :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
a x |
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Le tableau de variation sera :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
a x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
2°) On peut obtenir un tableau de
proportionnalité à partir d’une équation.
Soit l’équation y = 3x
1° )On trace le tableau :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
a x |
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
2°) on choisit des valeurs pour « x »
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
a x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y |
|
|
|
|
|
|
|
3°) on donne la valeur à
« a » , et l’on effectue tous les calculs
pour trouver « y ».
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
3 x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y = 3x |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
Conclusion :
Le tableau de proportionnalité représentant la fonction : y = 3x est :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
3 x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
Remarque : le tableau peut se réduire à 3 colonnes de
valeurs : ( suffisant pour tracer une droite)
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
3 x |
x |
|
-2 |
|
0 |
1 |
|
|
|
|
y |
|
-6 |
|
0 |
3 |
|
|
4° ) On peut obtenir un tableau de proportionnalité à partir
d’une représentation graphique.
Sur la droite on place des points que l’on
nomme : A ;B ; C ; O ;D ;E ;F Le
nombre de points est défini à partir de contraintes imposées ! !
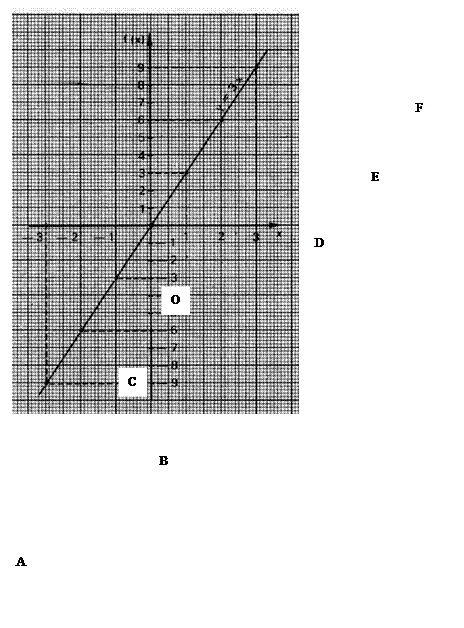
On trace le tableau :
|
|
A |
B |
C |
O |
D |
E |
F |
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Le tableau est « rempli » à partir des
résultats trouvés sur la droite :
Pour chaque point on relève son
abscisse et son ordonnée
|
|
A |
B |
C |
O |
D |
E |
F |
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
Les coordonnées du point A peuvent se noter
verticalement :
Comme
|
A |
- 3 |
|
|
-9 |
au lieu de
(de l’écriture horizontale) A (-3 ; -9 )
4°
Résumé : Plus généralement :
Modèle de tableau de proportionnalité :
|
|
|
A |
O |
|
B |
C |
|
D |
E |
|
|
|
|
relation |
x |
xA |
0 |
1 |
Valeurs choisies de la variable |
|
||||||
|
« ax » |
y |
yA |
0 |
a |
Valeurs «des « y » obtenues par calcul |
|
||||||
xA et yA sont
les coordonnées du point A
ces valeurs peuvent se noter verticalement :
![]() A xA ou horizontalement A (xA ,yA)
A xA ou horizontalement A (xA ,yA)
yA
TRAVAUX AUTO FORMATIFS.
1°) Que représente un « tableau de
variation »
?
2°) Que désigne le mot « variable » ?
3°) Représenter
le tableau de « proportionnalité ; précisez ce qu’il
« contient ».
1°) on donne l’ équation : y = 3x
, construire un tableau de proportionnalité
de 7 couples
on donne des valeurs à « x » ( exemples :
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
On effectue les calculs en remplaçant « x » par une valeur
numérique choisie et l’on rempli le tableau :
Ce qui nous nous donne le tableau suivant :
|
|
A |
B |
C |
O |
D |
E |
F |
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
2°)on nous donne le graphe suivant ; construire le
tableau de variation
G = { (
-3 ; -9) ; (-2 ;-6 ) ; (-1 ;-3 ) ; ( 0 ; 0
) ; (1 ; 3 ) ; (2
;6 ) ; ( 3 ;9 ) }
3°) Soit les fonctions établir pour chaque
un tableau de variation (minimum):
|
y1
= 2x |
y2
= - 2x |
y3
= - |
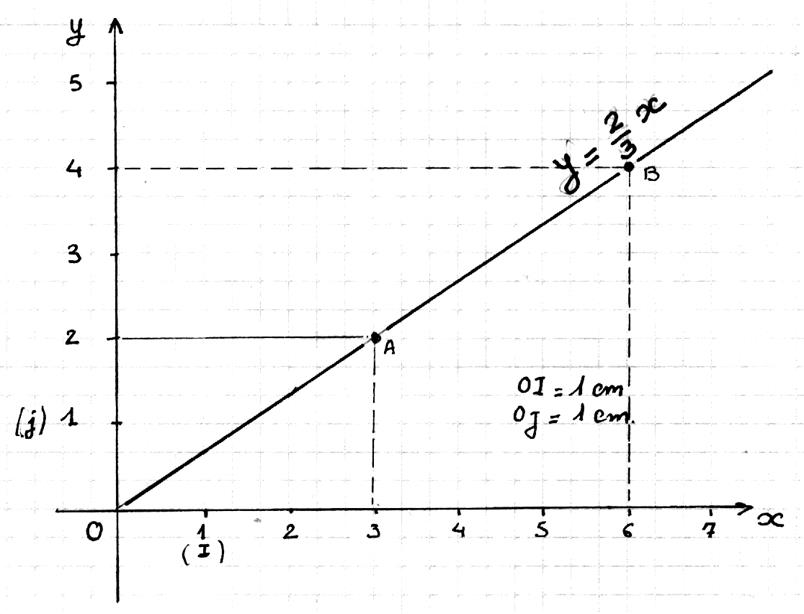
4° ) Soit le
représentation graphique d’une fonction linéaire construire un tableau :
tableau (minimal):
|
|
O |
A |
B |
|
x |
0 |
+3 |
+ 6 |
|
y |
0 |
+2 |
+ 4 |
|
|
|
Géométrie : |
|
|
|