Niveau :V

Objectif : DOSSIER : FONCTIONS AFFINES et les systèmes d’équations

Pré requis:

Méthodologie : rédiger….
Les droites : représentations graphiques
Fonction linéaire
Fonction affine
Fonction affine : les graphes
Fonction affine : applications.

Complément d’informations : Certaines parties de problèmes ci –dessous peuvent être traitées par le calcul ( notamment pour ce qui concerne la détermination des coordonnées du ou des points communs, s’ils existent ):

Lorsque nous avons deux droites sur un graphique on peut faire appelle à des connaissances supplémentaires :

Résoudre des systèmes d’équations du premier degré à deux inconnues.
Système d’équations (représentation graphique )
Pré requis :  « sciences »
Etude du mouvement uniforme.	►Autres activités

DOSSIER : Exercices et problèmes sur REPERAGE et interprétation de graphiques.

1°) Le graphique montre les déplacements de Denis et Patrick. Denis est à pied . Au bout de combien de temps a – t – il parcouru 5 km ? Quelle distance a – t - il parcouru quand il s’arrête au bout de 4 h ? Patrick : A quelle heure et à quelle distance du point de départ rencontre – t – il Denis pour la première fois ? Au bout de combien de temps rentre – t –il chez lui ? Combien de temps dure son retour ? Quelle est sa vitesse horaire ? Où et à quelle heure rencontre-il Denis pour la seconde fois ?

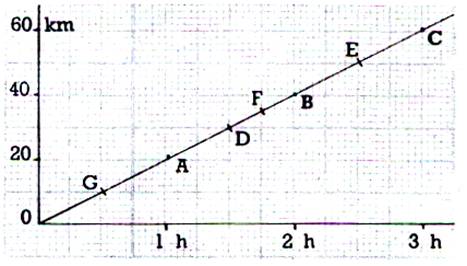
2°) Dans un système d’axes orthogonaux gradués régulièrement dont l’origine est le point O ( 0 ; 0 ) Placer les points A , B , C , D , E de coordonnées respectives ( +2 ; +2 ) ; ( -5 ; -5 ) ; ( +3 ; +3 ) ; ( +1 ; +1 ) ; ( -3 ; -3 ). Que peux –t –on dire de ces points ?

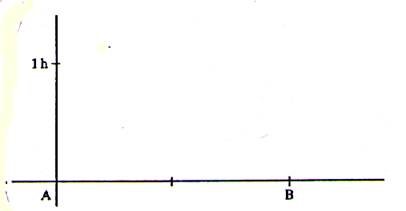
3°) Pour leur entraînement quotidien deux athlètes , Denis et Bertrand , parcourent 10 km. Denis court de A vers B à la vitesse moyenne de 8 km / h tandis que Bertrand court de B vers A à la vitesse moyenne de 7 km /h. a) En utilisant un repère du genre de celui de la figure ci contre représenter les courses de Denis et Bertrand. b) Déterminer sur le graphique à quelle distance approximative de A se situe leur point de rencontre .

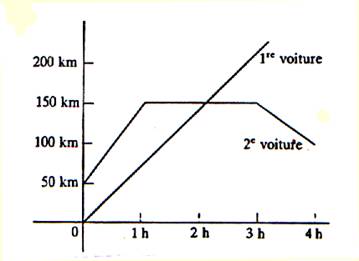
4 ° ) Traduire le graphique suivant :

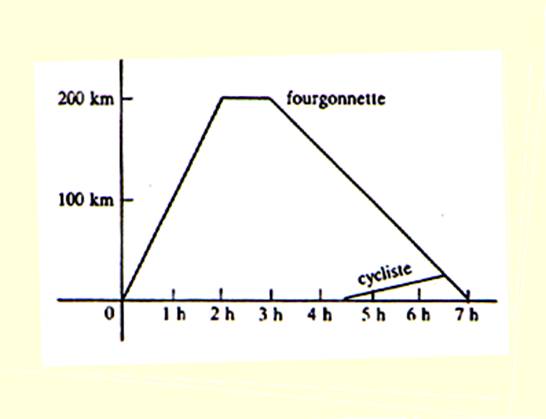
5° ) Traduire le graphique :

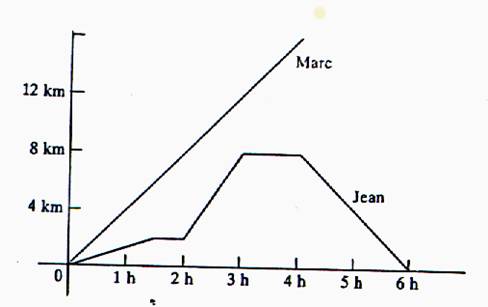
6° ) Sur ce graphique , on a représenté les déplacements à pied de Jean et de Marc. Répondre aux questions suivantes : Pour Marc : quel chemin a-t-il parcouru au bout de 2 heures ? de 3 heures ?*A quelle distance s’arrête – t – il ? Quelle distance a – t- il alors parcourue ? A quelle distance de l’arrivée était-il une heure et demie avant d’arriver ? Pour Jean : Au bout d’une heure et demie , quelle distance a-t-il parcourue ? et au bout de deux heures ? Après six heures de marche , il revient à son point de départ : quelle distance a – t –il parcourue alors ?Quelle a été la durée de ses arrêts ?

7° ) Dans un plan P , dessiner un système d’axes orthogonaux gradués régulièrement , placer des points ayant leur abscisse égale à leur ordonnée. Le point O est –il un point qui répond à cette hypothèse ?

Que peut-on dire de l’ensemble de ces points ?

Pouvez vous en donner le nom ?

8° ) Sur un quadrillage muni d’un repère orthonormé ( O, I , J ) placer les points A (+2 ;+1) ; B ( +3 ; +5 ) C ( +7 ; +2 )

On désigne par A’ le point de coordonnées ( Abscisse de A ; opposé de l’ordonnée de A)

Quelles sont les coordonnées de A’ ?

Utiliser la même méthode pour obtenir les coordonnées de B’ et de C’ à partir des coordonnées de B et C .

Placer les points A’ B’ C’ sur le quadrillage.

On désigne par A ‘’ le point de coordonnées (opposé de l’abscisse de A’ , ordonnée de A’)

Quelles sont les coordonnées de A’’ ?

Par la même méthode , à partir des coordonnées de B’ et de C’ on obtient les points B’’ et C’’.

Placer les points A’’ , B’’ et C’’ sur le quadrillage .

On a donc A ( +2 ;+1 ) a pour image A’ ( +2 ; …) qui a pour image ( … ; ..) à l’aide de ce modèle , faites la même chose pour les points B et C .

Pouvez vous donner la règle connaissant les coordonnées de A pour obtenir directement les coordonnées de A’’ ?

Cette règle s’applique – t – elle aux points B et B’’ ; C et C’’ ?

Mouvements uniformes :

Informations plus ++++

P b N°1

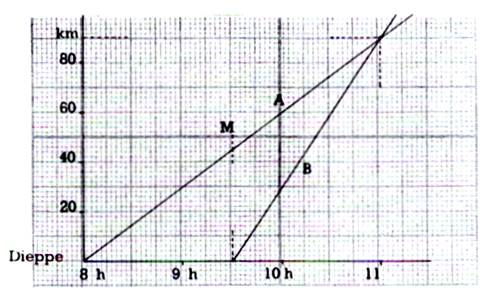
Le graphique ci-dessus représente le déplacement d’un cycliste (A) et d’un cyclomotoriste (B) s’éloignant tous deux de DIEPPE , sur la même route.

Dites pour chacun :

a) son heure de départ ;

b) sa vitesse par heure.

c) Quand part le motocycliste, le cycliste est en « M » :quel est son avance sur le motocycliste (en km) ? vérifier par le calcul ;

A quelle heure le cycliste est-il rejoint ? A quelle distance de DIEPPE ?

Pb 2

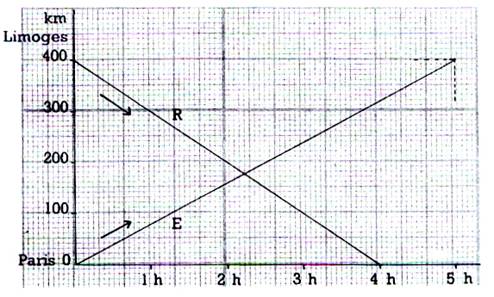
Le graphique ci-dessus représente la marche de deux trains : un rapide « R », qui va de Limoges à Paris , un expresse « E » qui va de Paris de Paris à Limoges , et qui partent en même temps.

a) Quelle est la vitesse de chacun ? Le calcul , en examinant les distances et les heures d’arrivées , vous donne-t-il le même résultat que l’examen graphique ?

b) Au bout de combien de temps se croisent-ils ? A quelle distance de Paris ? de Limoges ?

A quelle distance de Paris se trouve l’express quand le rapide arrive à Paris ? (vérifiez par le calcul)

Pb 3

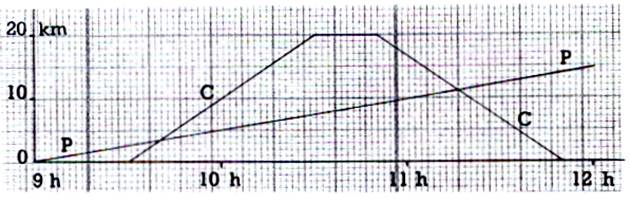
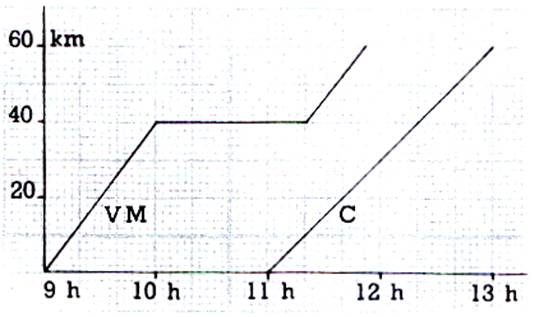
Le dessin ci-dessus représente le déplacement de deux mobiles partis du même village , dans la même direction , mais à des heures différentes :

1°)un piéton (P) qui va voir ses parents à 15 km de là , et qui marche régulièrement , sans s’arrêter ;

2°) un cycliste ( C) qui , roulant régulièrement , va à la ville voisine , y reste 20 mn , et revient à la même allure .

a) Quelles sont les heures de départ ?

b) Quelle est la vitesse de chacun ?

Quand , comment et à quelles distances du village de départ le cycliste rencontre-il le piéton ?

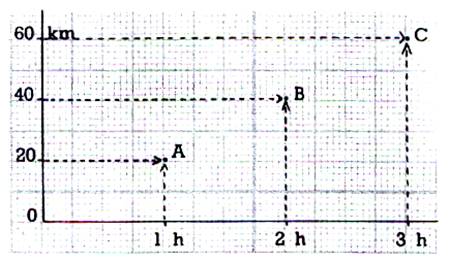
Exercices : pour les 3 graphiques suivants , imaginer une situation problème et la rédiger ; faire les calculs si nécessaire .

Commentez !