|
|
|
3ème Collège. |
|
|
Pré requis: |
|||
|
1°) le premier
degré : résolution d'équations types. Et Problèmes résolus. |
CORRIGE certains sont à finir |
||
ENVIRONNEMENT du dossier:
|
Objectif précédent : 1°) comment
traiter un problème .
|
Objectif suivant : 2°) Problèmes d’application
.impossible ; indéterminé, inacceptable . |
tableau 2°)Présentation
des cours et travaux du premier degré |
Fiches : Résolution de problèmes équations.
|
|
|
|
|
|
|
Fiche 1 : Résolution de problème. |
|
|
|
|
Fiche
2 : Equations. |
|
|
|
|
Fiche
3 : Résolution de problèmes – Interprétation de résultats |
|
|
|
|
Fiche
4 : Situations particulières. |
|
|
|
|
Fiche 5 : Equation de la forme : « a x + b = 0 » |
|
|
|
|
Fiche
6 : Résolution d’équations. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fiche 1 : Résolution de problème. |
|
|
|
|
Situation problème : Pierre , Léonie, Simon viennent de faire un héritage . Voici le
testament : La part de Léonie est égale à 5000 € plus deux
fois la part de Pierre. La part de Simon plus 30 000€ est égale à 4
fois la part de Pierre. La part de
Léonie est le triple de la part de Simon. Combien chacun des héritiers doit-il
recevoir ? |
|
|
|
|
Pour résoudre ce problème ,
vous procédez comme vous l’avez fait en 4ème. |
|
|
|
|
1°) Choix
de l’inconnue :
Appelons « 2°) Mise
en équation : C’est la traduction de l’énoncé en langage mathématique. « «
la part de Léonie (
en € ) est » : « La
part de Simon « plus » 30 000€
est égale à 4 fois la part de Pierre. » : se traduit
par :
soit la part de « La
part de Léonie est le triple de la
part de Simon » ce qui se traduit par : 3°)
Résolution de l’équation : (il ne
vous reste qu’à résoudre cette équation , comme vu en 4ème )
-
La part de Pierre est
de 9 500 €. -
Part de Léonie :
5 000 + 2 (
9500) = 5 000
+ 19 000 =
24 000 € -
Part de
Simon : 4 -
vérification : 4°)
Réponse a la question du problème : |
|
|
|
|
part de Pierre : 9 500 €. part de Léonie : 24 000 €. part de Simon : 8 000€ |
|
|
|
|
|
|
|||
|
|
Fiche 2 : Equations |
|
|||
|
|
Activités : Résolvez, comme vous l’avez fait
en 4ème , les équations d’inconnue
« |
|
|||
|
|
Equation 1 |
|
|
|
|
|
Equation 2 |
|
|
|||
|
Equation 3 |
|
|
|||
|
Equation 4 |
|
|
|||
|
|
|
|
|||||
|
|
Fiche 3 : Résolution de problèmes –
Interprétation de résultats. |
|
|
||||
|
|
Voici quatre problèmes qui se ressemblent par leur
énoncé mais qui sont bien différents par la réponse à la question posée. |
|
|||||
|
|
|
|
|||||
|
|
Problème 1 : Un père à
42 ans , son fils à 12 ans . Ils ont leur
anniversaire le même jour. Dans combien
d’années, l’âge du fils sera-t-il le tiers de l’âge du père ? |
|
|||||
|
|
1°) Choix
de l’inconnue : appelons « 2°) Mise
en équation .
Dans « « l’âge
du fils est le tiers de l’âge du père » se traduit par : .. 3°)
Résolution de l’équation : |
|
|||||
|
|
|
|
|
|
|||
|
|
4°) Réponse à la question du problème : Comme « |
|
|||||
|
|
Problème 2 : Un père à
42 ans , son fils à 12 ans . Ils ont leur anniversaire
le même jour. Dans combien d’années, l’âge du fils sera-t-il le
quart de l’âge du père ? |
|
|||||
|
|
1°) Choix
de l’inconnue : appelons « 2°) Mise
en équation .
Dans « « l’âge
du fils est le tiers de l’âge du père » se traduit par : .. 3°) Résolution de l’équation : |
|
|||||
|
|
|
|
|
|
|||
|
|
4°) Réponse à la question du problème : Comme « |
|
|||||
|
|
|
|
|||||
|
|
Problème 3 : Un père à
42 ans , son fils à 12 ans . Ils ont leur
anniversaire le même jour. Dans combien d’années, l’âge du fils sera-t-il le
|
|
|||||
|
|
1°) Choix
de l’inconnue : appelons « 2°) Mise
en équation .
Dans « « l’âge
du fils est le tiers de l’âge du père » se traduit par : .. 3°) Résolution de l’équation : |
|
|||||
|
|
|
|
|
|
|||
|
|
4°) Réponse à la question du problème : Comme « Le problème n’a pas de solution car au bout de
258 ans , le père et le fils seront
« mort » depuis longtemps. |
|
|||||
|
|
Problème 4 : Un père à
42 ans , son fils à 12 ans . Ils ont leur
anniversaire le même jour. Dans combien d’années, l’âge du fils sera-t-il le
|
|
|||||
|
|
1°) Choix
de l’inconnue : appelons « 2°) Mise
en équation .
Dans « « l’âge
du fils est le tiers de l’âge du père » se traduit par : .. 3°) Résolution de l’équation : 4°) Réponse à la question du problème. Le nombre trouvé n’est pas ……………..donc le problème
…………………………………………………. ( Il n’est même pas possible de donner un
nombre entier de jours , expliquez pourquoi ) . |
|
|||||
|
|
|
|
|
|
|
Fiche 4 : Situations particulières. |
|
|
|
|
Problème 1 : Paul, Victor et Lison ont leur anniversaire le
même jour. Paul à 14 ans , Victor
17 ans et Lison 25 ans. Dans combien d’années la somme des âges de Paul
et de Lison sera-t-elle égale au double de l’âge de Victor. |
|
|
|
|
1°) Choix
de l’inconnue : Appelons « 2°) Mise
en équation. -
Dans « x » années , l’âge de Paul
sera ……………………………. -
Dans « x » années , l’âge de Victor
sera ……………………………. -
Dans « x » années , l’âge de Lison
sera ……………………………. « La
somme des âges de Paul et de Lison est
le double de l’âge de Victor se
traduit par : ………………….+
………………...= 2 (……..) 3°)
Résolution de l’équation. |
|
|
|
|
|
|
|
|
|
Quel que
soit le nombre mis à la place de « On aboutit
alors à l’égalité « Donc
cette équation n’a pas de solution. 4°)
Réponse à la question du problème. |
|
|
|
|
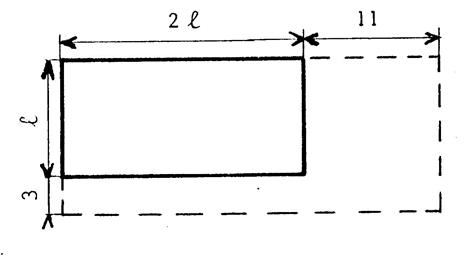
Problème 2 : |
|
|
|
|
Partant d’un
rectangle dont la longueur est le double de la largeur, on augmente la
longueur de « 11 m »et la largeur de « 3m ». On
voudrait obtenir un nouveau rectangle dont la longueur surpasse de
« 5m » le double de sa largeur. Quelle
doit-être la largeur du rectangle initial ? |
|
|
|
|
1°)
Choix de l’inconnue : appelons « l » la
largeur ( en mètre) du rectangle initial. |
|
|
|
|
2°)
Mise en équation : -
Longueur du rectangle
initial :…….. -
Largeur du nouveau
rectangle. : ………………. -
Longueur du nouveau
rectangle : ………………………………………….. La longueur surpasse de « 5 m » le double de sa
largeur » se traduit par : ………………………….= 2 ( ……..)
+ …….. 3°)
Résolution de l’équation. Quel que soit
le nombre mis à la place de « l » , «0 l = 0» est toujours ……………………………donc tous les
nombres sont solutions de l’équation. 4°)Réponse à la question du problème. : …………………………………………………………………………………………………………….. |
|
|
|
|
Fiche
5 : Equation de la forme : « a x + b = 0 » |
Info ++@ :égalité l’on a transposé |
|
||||
|
|
|
|
|||||
|
|
Exemple 1 :
Résolvons l’équation de la forme :
Ta sais
que « A = B » a la même signification « A – B = 0 » L’équation
donnée a donc les mêmes solutions que l’équation : On dit
que l’on a transposé
« Transformons
l’écriture du premier membre , pour cela : Développons :
…… Réduisons
les termes semblables : …… On obtient
alors une équation qui a les mêmes solutions que l’équation donnée et qui est
de la forme « |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
||||
|
A les mêmes solutions que « On divise
les deux membres par « 5 ». L’équation
a pour solution : |
« a »
les mêmes solutions que « Si L’équation
a pour solution unique |
||||||
|
|
v
Que se passe-t-il si
« a = 0 » ? ( on a déjà étudié ce cas dans la fiche 4) |
|
|||||
|
|
|
|
|||||
|
|
Exemple 2 :
Résolvez l’équation : |
|
|||||
|
|
En
transposant : En
développant : On a
alors … |
|
|||||
|
|
Exemple 3 : Résolvez
l’équation : |
|
|||||
|
|
En
transposant on obtient
: |
|
|||||
|
|
En
développant on obtient : |
|
|||||
|
|
Quel que
soit le nombre mis à la place de « z » ; |
|
|||||
|
|
On
énoncera alors le théorème : |
|
|||||
|
|
Théorème : Etant
donné l’équation « -
Si « a -
Si « |
|
|||||
|
|
|
|
|||||
|
|
Activité n°
………Exercice : Vous
devez être capable de résoudre instantanément les équations suivantes : |
|
|||||
|
|
2
|
Solution :
…………………… |
«
- 5 x
+ 4 = 0 » |
Solution :
…………………… |
|
||
|
|
Solution :
…………………… |
« - 6v x – 5 = 0 » |
Solution :
…………………… |
||||
|
|
Quelle
remarque pouvez-vous faire à propos des signes ? ( verbalement) |
|
|||||
|
|
v
Désormais ,
toutes les fois que c’est possible , après avoir transposé , essayiez de vous
ramener à une équation de la forme : |
|
|||||
|
|
|
|
|||||
|
|
Activité n° ……. : Résolvez l’équation : |
|
|||||
|
|
1° ) Vous transposez :
…………………………………………………………………………… 2°) Vous développez :
……………………………………………………………………………… 3° )
Vous réduisez les termes semblables : ……………………………………………………… 4 ° )
L’équation a alors pour solution : ……………………………………………………………….. |
|
|||||
|
|
Fiche
6 : Résolution d’équations. |
|
|
||
|
|
Exemple
1 : Vous allez résoudre
l’équation : En
multipliant les deux membres de l’équation par un même nombre, on obtient une
équation qui a les mêmes solutions. Multiplions
alors les deux membres par un multiple des dénominateurs. Pour que
le calcul soit le plus simple possible , il est
préférable de choisir un multiple commun le
plus petit possible . Vous choisissez …… »12 »….. On
obtient alors : : En
développant, on obtient : Et après
simplification, on obtient : L’équation
possède la solution unique : |
|
|||
|
|
Exemple 2 : Résolvez
l’équation : |
|
|||
|
|
2 façons
peuvent être utilisées : le produit en croix ou passer par le multiple
commun des dénominateurs ……. |
|
|||
|
|
Le
multiple commun des dénominateurs le plus petit possible est : ..10 ….. Multipliez
les deux membres de l’équation par ce nombre , vous
obtenez :
Après simplification , il reste : Finissez
la résolution :
|
|
|||
|
|
: le produit en croix : |
|
|||
|
|
Exemple 3 : Résolvez
l’équation : Le
multiple commun des dénominateurs le plus petit possible est : ..18 ….. Multipliez
les deux membres de l’équation par ce nombre , et développez vous
obtenez :
Attention :
n’oubliez pas qu’un trait de fraction tient lieu de parenthèses. Prés
simplification, il reste : Développement : L’équation
possède une solution unique : |
|
|||
|
|
|
|
|||
|
|
Exemple 4 : Résolvez l’équation : Vous
multipliez les deux membres par
« 6 » .
Après simplification , il reste : Finissez la résolution ………… |
|
|||
|
|
|
|
|||
|
|
Activités
« exercices » …….. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|||
|
|
|
|
|
|
Fiche
7 : Situations problèmes. |
|
|
|
|
|
|
|
Problème 1 La contenance totale de trois tonneaux est 177
L ( litres) La contenance
du deuxième est les deux tiers de celle du première .
Le troisième contient 15 L de moins que le
premier. Déterminez la contenance de chacun des tonneaux. |
|
|
|
Problème 2 Des enfants
collectionnent des timbres-poste. Eric a 537 timbres
de plus que David Si Eric
donne 43 timbres à David, Eric a alors deux fois
plus de timbres que David. Calculez
le nombre de timbres que possédaient initialement Eric
et David. |
|
|
|
Problème 3 Un enfant joue aux billes. Il perd 6 billes
puis le tiers de ce qu'il lui reste et
enfin il en perd encore 8. 11 lui reste alors les deux cinquièmes de ce qu'il
avait au départ. Combien avait-il de billes initialement ? |
|
|
|
Problème 4 Deux villes
A et B sont distantes de 48 km. Un
cycliste "a" part de A en
direction de B. Au même moment, un cycliste "b " part de B à
la rencontre de a. La vitesse moyenne de « a » est les
A quelle distance de A se rencontreront
- ils ? Indication :
La vitesse de a étant les |
|
|
|
Problème
5 : Arnaud, Benoît et
Caroline se partagent une somme d'argent. La part de Benoît est les La part de Caroline est les Sachant que Caroline a reçu 5400 € de plus que Benoît, détermine la part de
chacun. |
|
|
|
Problème 6 (D'après Brevet Créteil 88) La
largeur d'un rectangle est 3 cm . On augmente la
longueur et la largeur de ce rectangle de 2 cm .
L'aire du nouveau rectangle est supérieure de 20cm à celle du rectangle initial. Quelle est la longueur du rectangle
initial ? |
|
|
|
Problème 7 Un bassin
est plein. On en vide le quart ,
puis le tiers du reste et enfin la moitié
du nouveau reste. Sachant qu'il y a encore 230 L dans le bassin, quelle est la
contenance de ce bassin. |
|
|
|
Problème 8 Un voyageur part en train d'une ville A
vers une ville B a la vitesse moyenne de 90km/h . Il revient de B vers A en automobile par un trajet de
20km de plus qu'en train à la vitesse
moyenne de 70km/h . Sachant que la durée totale aller retour a été
de 6 h , détermine la longueur du trajet en train de
A à B, Indication Evalue
le temps passé dans chacun des deux trajets.
, Si « d » est la distance, « v » la
vitesse et « t » le temps,
v = |
|
|
|
Problème 9 Un cycliste monte une côte à La vitesse de
15km/h . Il
la descend à la vitesse de 40km/h . Sachant qu'il met
un quart d'heure de moins à la descente qu'à la montée, détermine la longueur
de la côte. Indication
Evalue le temps passé en montée et en descente comme au problème 8. |
|
|
|
Problème 10 J'ai trois fois
l'âge que j'aurai dans trois ans diminué de trois fois l'âge que j'avais il y a trois ans. Quel est mon âge ? |
|
|
|
|
|