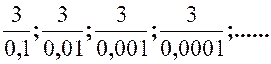1°)   Symbole : «  » 

2°)  Symbole :  «  » 

3° ) forme :

Il arrive quelque fois qu’une fraction , pour certaines valeurs particulières assignés aux lettres qu’elle contient , voit s’annuler son numérateur ou son dénominateur ou même l’un et l’autre , et prend une des formes : «  » ; «  » ; «  » .

Nous allons chercher le sens de ces formes singulières , après s’être imprégné des notions sur l’infini et sur ces limites.

Symbole : «  » 

Proposition - Toute fraction «  »  dont le numérateur est nul sans que le dénominateur  soit nul  ( ni infini) , est nulle.

En effet, soit « x » la valeur de cette fraction. Une fraction étant l’expression d’un quotient , les égalités «  = x »  et  «  m x = 0 » sont équivalentes.

 Or, pour que le produit de deux quantités déterminées soit nul , il faut et il suffit qu’un des facteurs le soit.  Donc si « m » est une quantité déterminée différente de zéro , « x » est nul.

Si « m » était nul , la fraction «  »   serait de valeur indéterminée. ( à démontrer !!!!)     

Info ++

Symbole : «  » .

Proposition - Toute fraction de la forme «  » .le numérateur « m » désignant une quantité  déterminée et différente de zéro et le dénominateur  « 0 » désignant une quantité non pas rigoureusement nulle, mais infiniment petite est le symbole de l’infini.

En effet , un quotient dont le dividende est constant et dont le diviseur décroît indéfiniment , croit lui-même indéfiniment en proportion inverse ;

Ainsi , les rapports :  ont pour valeurs respectives :  «  30 ; 300 ; 3 000 ; 30 000 ; …. ».

Par conséquent , une fraction dont le dénominateur est infiniment petit est elle- même infiniment grande …

Remarques :

N°1 :  Il importe de ne point perdre de vue que si l’on considère   comme symbole de l’infini  , le dénominateur « 0 » ne désigne point le zéro habituel , mais une quantité infiniment petite , une quantité variable décroissant indéfiniment et s’approchant d’aussi prés qu’on veut de la valeur limite de zéro.

N°2 : Si le dénominateur est actuellement « nul » , la fraction  cesse d’exister.

Il n’existe , en effet, aucune quantité « q » qui satisfasse à la relation  = q ; c'est-à-dire qui , multipliée par zéro , donne un produit « m » différent de zéro. La division  est d’une impossibilité absolue .  ( voir division algébrique : division possibles et impossibles) ;          ( voir les cas particuliers de  la division des entiers ….à mettre en rappel  )

Le symbole  à dénominateur nul , est donc le symbole d’une quantité impossible à réaliser.

N°3 :  En considérant « 0 » comme le symbole d’une quantité non pas nulle, mais s’approchant indéfiniment de zéro , on peut donner à zéro « 0 » le signe .

Par « + 0 », on désigne donc la limite d’une quantité positive indéfiniment décroissante , et par «  - 0 » la limite d’une quantité  négative dont la valeur absolue décroît indéfiniment ; en d’autres termes , « + 0 » représente une quantité positive infiniment petite , et « - 0 » une quantité négative infiniment petite.

D’après cela , en désignant « + »  l’infini positif , c'est-à-dire une quantité infiniment croissante , et par  « - »  l’infini négatif , c'est-à-dire une quantité infiniment  croissante , en valeur absolue , et en supposant « m » positif , on écrira : =   +    et   =   -

3° ) forme « indétermination »   :

Réponse :   Cliquez ici pour plus d’informations…………..

Refaire les exercices du cours……