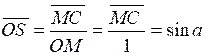Pré  requis: 

Lectures :1°) notions sur les dérivées
2°)  Notions sur  les dérivées.
3°) Signification géométrique de la dérivée.

 

Index  warmaths	Objectif précédent     1°) Dérivée de la forme ax² + bx + c 2°) le cercle trigonométrique.	Objectif suivant   1°) Applications de la dérivée.  2°)  Cours de niveau IV 3°) La fonction trigonométrique.	Tableau :       1°) liste des informations sur La trigonométrie. 2°)  LES DERIVEES.

Lecture : DOSSIER: DERIVEES des fonctions  trigonométriques.

1.      Théorème préliminaire :

2.    Dérivée de y = sin x

3.     Dérivée de y = cos x

4.    Dérivée de y = tan  x

 

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

 

COURS

 

 

 

Pré requis :  en radians Le cercle trigonométrique.
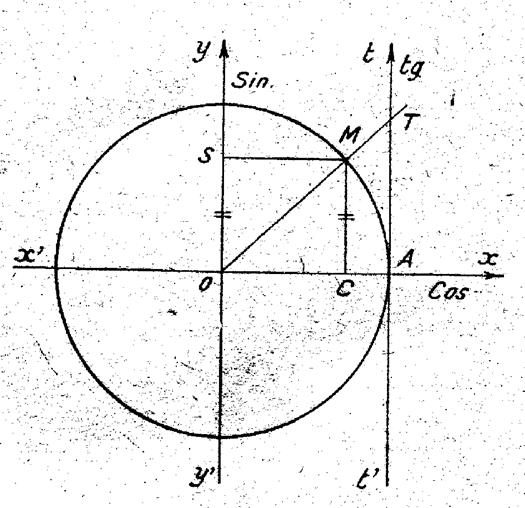
Théorème préliminaire :     Si  l’arc « a »  est exprimé en radians ; sin « a » tend vers « a » lorsque « a » tend vers « 0 ».   Soit  l’ arc  AM  =  a   exprimé en radians , nous déterminons le sinus et la tangente de cet arc.   *  =  sin a   * remarque       ( OM = Rayon =1)   et      = tg. a

 

Nous avons :

       CM  <  arc AM  < AT

                                     Or                         CM = OS                  d’ où 

 

 <  arc AM  <

 

soit

sin a  <  arc AM  <  tg a

 

ou en tenant compte de l’égalité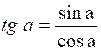   

 

sin a  <  a  <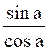

 

divisons tous les termes par   sin a  ,  nous obtenons :

1   <     < 

 

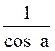
Si « a » tend vers  zéro , cos a  et par conséquent 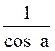    tend vers 1 ;

 

 

Etant limité de part et d’autre par  1 ;      tend vers 1 , autrement dit , sin a  tend  vers « a ».

 

Dérivée de y = sin x

 

( ou autre écriture :  f (x) = sin x )

 

Soit x _O , une valeur fixe de « x » ,  nous lui donnons un accroissement «  delta x » , noté :  x ;

L’accroissement correspondant de « y »   ( noté :    y ) est :

 

 y  =  sin (x _O  +  x)   -  sin  x _O  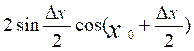=                                 ( rappel …@ )

 

donc : 

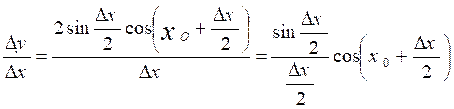
Quand  x  tend vers zéro,

-   le premier facteur tend vers « 1 »                                  ( théorème fondamental : quand « x » tend vers  zéro , 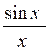  à pour limite « 1 ») …………..voir le précis d’algèbre………….)

 

-            Et le second facteur  tend vers cos x₀  .

-            Donc        a donc pour limite cos x₀ 

 

-            Si on ne précise pas la valeur de x₀  , on voit que :   y = sin x    a pour dérivée    y’ = cos x

 

Dérivée de y = cos x

 

Un calcul analogue montre que : 

 

-            Si on ne précise pas la valeur de x₀  , on voit que :   y = cos  x    a pour dérivée    y’ = - sin x

 

 

Dérivée de y = tan  x

 

 

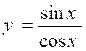
donc ( dérivée  d’un quotient)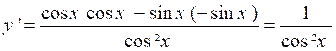

 

donc  y = tan x   a pour dérivée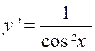 

 

Dérivée de y = cotan  x

 

On trouvera de même que  y =cotan x   a pour dérivée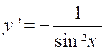 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CONTROLE : aucun travail de prévu.

Savoir  énoncer les règles.

EVALUATION:

Il faut savoir refaire les exercices du cours.