|
TRAVAUX AUTO -
FORMATIF |
N°9 / 25 |
CORRIGE |
||
|
CONSIGNE : vous
devez répondre aux questions en vous aidant du cours . |
||||
|
N°9 |
LA PROPORTIONNALITE et les calculs sur la
proportionnalité ;son
l’application linéaire . Etude chapitre par chapitre (des questions
peuvent être rajoutées): |
|||
|
|
||||
Prendre une feuille , répondre
aux questions en vous aidant du cours.
|
VOCABULAIRE
déjà utilisé : (Rappels) |
I ) Qu’appelle t - on : Rapport ?:
On appelle « rapport » : le
quotient obtenu par la division d’un nombre par un autre nombre.
Quel est le modèle mathématique d’un
« rapport » ? le modèle est « une
écriture fractionnaire ou une
fraction ».
Compléter le tableau :
|
Exemples : |
Quotient : |
Commentaire : |
|
6 / 2 = 3 |
3 |
Le quotient est un nombre entier. |
|
4,5 :2 = |
2,25 |
Le quotient est un nombre décimal |
|
8 : 3 |
|
Le quotient est une
fraction irréductible dit « rationnel » |
II ) qu’appelle -t - on
« Rapports égaux » ? :
On appelle « rapports égaux » des
divisions qui ont le même quotient ( et dont le reste des divisions est
identique ) .
- quel est le modèle
mathématique de deux rapports égaux est l’égalité de deux fractions ?.
|
- Traduction en
langage mathématique : |
|
Quel peut être la nature du quotient ? peut être un nombre
entier, un nombre décimal ou une
fraction .
III ) Qu’appelle -t - on
par « Suite de rapports
égaux » ?
Lorsque nous avons
plus de deux rapports égaux nous pouvons
dire que nous avons une
« suite de rapports égaux » , le quotient de chaque rapport étant
identique , ce quotient est un nombre de
valeur « constante » , on
l’appelle « k » (coefficient).
-Quel est son modèle mathématique ? Traduction en
langage mathématique :
![]()
Appliquer : ![]() sont t-ils des
rapports égaux ?
sont t-ils des
rapports égaux ?
![]() on trouve le même quotient donc k = 5
on trouve le même quotient donc k = 5
FIN du rappel.
|
La
proportionnalité : |
|
Info plus !! et :i |
1°) Donner la définition de la
proportion ??? :
Définition :-
L'égalité de deux rapports est appelée "une proportion".
- On appelle « proportion »
l’égalité de deux rapports.
2°) Soit deux cas : montrer si il y a , ou pas , une proportion :
|
Cas : il y a proportion |
|
Cas il n’y a pas proportion |
|
|
|
|
|
Réponse : |
Réponse : |
|
|
Réflexion : Si
le quotient des divisions sont identiques , nous avons une proportion. |
Réflexion
Si le quotient des divisions sont
identiques , nous avons une proportion. |
|
|
Calculs : 9 : 3 = 3
; 18 : 6 = 3 Etude du résultat du
calcul : le quotient est
identique , le reste = 0 |
Calculs : 9 : 3 = 3 ; 27 ; 3 = 9 Etude du résultat du
calcul : le quotient est n’est
pas identique . |
|
|
Conclusion : Les deux fractions forment deux
rapports égaux c’est une proportion. |
Conclusion : Les deux fractions ne forment pas deux rapports égaux ; ce
n’est pas une proportion. |
3°) Compléter
la phrase : Lorsque le quotient « semble
identique) est identique et que le calcul ne « tombe pas juste (c’est à
dire que reste différent de zéro
) » Une autre possibilité de calcul permet de vérifier si deux fractions
sont égales : il faut calculer le « produit
en croix » . ( on verra cette pratique plus loin dans le cours
) .
4°)
Application : calculer le produit
en croix des deux fractions 8 / 3
et 16 / 6 ![]()
Les
produits de ( 8 ![]() 6 =
48 )
et (16
6 =
48 )
et (16 ![]() 3 =
48 )
sont appelés "les
produits en croix".
3 =
48 )
sont appelés "les
produits en croix".
5°) Soit la proportion : ![]() ; nommer les
« moyens et les extrêmes » les nombres
« 8 » et « 6 » sont appelés "les
extrêmes" et les nombres
« 3 » et « 16 » sont appelés "les moyens".
; nommer les
« moyens et les extrêmes » les nombres
« 8 » et « 6 » sont appelés "les
extrêmes" et les nombres
« 3 » et « 16 » sont appelés "les moyens".
6°)
compléter la phrase suivante :
Dans une
proportion le produit des extrêmes est égal au produit
des moyens.
Rappel C
d : les fractions
équivalentes :
6°)
Application : : ![]() est - elle égale à
est - elle égale à ![]() ? donner une conclusion .
? donner une conclusion .
Solution : « oui » si 3 fois 37,5
est égal à 15 fois 2,5 ;
Calcul n°1: 3
fois 37,5 = 112,5 ; calcul n°2 15 fois 7,5 = 112,5
Conclusion :
on trouve pour les deux multiplications le même produit « 112,5 » ;
on peut écrire que ![]()
7°) Qu’est qu’un coefficient de proportionnalité ?
Définition : Le
coefficient de proportionnalité est un nombre obtenu en divisant plusieurs fois deux
nombres différents , mais dont on trouve le même quotient .
8°) Quel
peut être la nature de ce nombre ( à
quel ensemble appartient -il ?) :
« entier » ;
« décimal » , « rationnel » , et relatif ou
pas relatif
9°) comment obtient - on un coefficient de proportionnalité
.. ce nombre est obtenu par un calcul : ce
calcul est une division . On obtient ce coefficient lorsque
l’on divise chaque valeur de la première suite par le nombre correspondant ( valeur
correspondante : qui occupe le même rang ) de la seconde suite .
10) Exemple
Si deux
suites de nombres forment une suite de nombres proportionnels : si
l’on met ces nombres dans un tableau , on obtient un tableau de
proportionnalité.
Le tableau ci dessous est appelé « tableau de proportionnalité »
|
´ 2 |
¯ |
1,5 |
4,3 |
9,6 |
Dans cette Ligne
supérieure les nombres forment la
« Première suite » |
¸2 |
|
3 |
8,6 |
19,2 |
Dans cette Ligne
inférieure les nombres forment la
« seconde suite » |
11 ) Quelle est la
valeur du coefficient de proportionnalité : 2 est le Coefficient de
proportionnalité
12°) Etablir la suite de nombres proportionnels et Vérifier ar le produit en croix :
3 / 1,5 ; 8,6 / 4,3 ;19,2 /9,6
; On a bien
4,3 ![]() 2 =
8,6 et 9,6
2 =
8,6 et 9,6![]() 2 = 19,2
2 = 19,2
13°) Lorsque l’on a deux suites de nombres , donner la règle qui permet
de calculer le coefficient de
proportionnalité !
Lorsque l’on a deux suites de
nombres ; Le coefficient de proportionnalité est égal au rapport des nombres
de la deuxième suite aux nombres correspondants de la première suite
de nombres.
|
.i9 |
III )
Rechercher si deux suites de nombres
forment une suite de nombres proportionnels |
14°) Quelle condition faut -il remplir
pour que deux suites de nombres forment une suite de nombres proportionnels. ?
Définition : Deux suites de nombres
forment une suite de nombres
proportionnels (rapports égaux) si le rapport entre les nombres de la
première suite et les nombres correspondants (même classement dans la suite )
de la deuxième sont constant . ( même valeur )
15°) Soit la première suite S1 = {
2 ; 6 ; 10 } ; soit la
deuxième suite S 2 = {
4 ; 12 ; 20 } , sont - elles
proportionnelles ?
1ère
Solution : si 2/4
= 6 / 12 = 10 /20
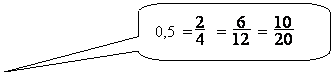 si {
2 ; 6 ; 10 } et { 4 ;
12 ; 20 } sont deux suites de
nombres proportionnelles car en faisant une simplification (ou calcul) des rapports on peut montrer que
si {
2 ; 6 ; 10 } et { 4 ;
12 ; 20 } sont deux suites de
nombres proportionnelles car en faisant une simplification (ou calcul) des rapports on peut montrer que
![]() ;
; ![]() ;
;
![]() deviennent
deviennent
![]() ;
;
![]() donne un nombre constant 0,5
donne un nombre constant 0,5
Vocabulaire : compléter la phrase :
16°) on dit aussi q ‘ une « équation » est une « écriture algébrique »
17 °) .iLa fonction linéaire est le modèle algébrique permettant de traiter toutes les
situations problèmes de la
proportionnalité.
18°) Problème « exemple » : 2 kg de
pommes valent 1, 6 € ; 3 kg valent 2,4 € ; 5 kg valent 4 € .
18a ) comment montrer qu’il y a
« proportionnalité » ? .
On montre qu
‘il y a proportionnalité en effectuant
les divisions suivantes :
(1,6 ¸2 ; 2,4 ¸ 3
et 5 ¸ 4) ; ce qui nous permet d’écrire la suite de nombres
« proportionnels » :
|
|
=
0,8 (0,8 étant le prix au kilogramme) |
18b ) compléter la phrase : On peut dire que
le prix à payer est égal à 0,8 €
multiplié par le nombre de kilogramme acheté.
18c)Que désigne la lettre
« y » ? : on désigne par « y »
le prix à payer ;
18d) Que désigne la
lettre « x » ? on désigne par « x » le nombre de kilogramme acheté
18e) On remplacera la formule de la forme y = a x
par l’équation :?? y = 0,8 x
18 f) Si le kilogramme de
pomme passe à 1,2 € le kilo ; donner
la formule : y = 1,2 x
Qu’est ce que
cela implique dans le raisonnement de celui qui achète ? prendre une
valeur numérique.
19 ) Donner le forme de
la formule ( forme algébrique)
y = a x ;
20) Compléter la
phrase : la droite d’équation
« y = 1,2x » peut être tracée dans
un repère cartésien.
21) « vocabulaire » : traduire l’écriture : f (x) :
lire
« en fonction de « x »
22 ) Compléter la phrase : o n dit que
« y » est obtenu en … f (x) ……..
23 ) Compléter la phrase : On remplacera l’équation « y = 1,2 x » et l’on écrira que la fonction s’écrira : « f(x) = 1,2
x »
+Généralisation : On
peut mettre les suites de nombres précédents sous la forme d’
![]()
![]() une suite de rapports égaux
une suite de rapports égaux ![]() =
=![]() =
=![]() =......... ;
=......... ;

On peut dire que cette
suite est égale au rapport des ![]()

Ce rapport est un
coefficient qui est égal au nombre que
l’on nommera « a » .
On peut donc écrire que : ![]() =
=![]() =
=![]() =
= ![]()
On a
décidé de transformer ces
rapports de la forme ![]() par
l’écriture y = ax
par
l’écriture y = ax
c’est une autre
forme d’écriture dite
« algébrique », cette écriture algébrique est une égalité appelée « équation » .
25 ) Cette
équation « y = a x » est appelée : « équation de la fonction linéaire » .
+Application à des cas concrets
(Adapté à la vie quotidienne)
D’autres
applications seront traitées dans le cours
10 /25 .
Série 1 :
26 ) ►Problème
1°)
Le prix d’un kg de
fruit est de 0,8 €. Donner une formule permettant de calculer le prix à payer
en fonction de la masse achetée.
Solution
Pour tout achat de ces
fruits , on a :
prix à payer = prix
au kg ![]() nombre
de kg
nombre
de kg
22a) Si on appelle
« x » le nombre de kg achetés
et « y » le prix à payer
on écrira l’équation
y = 0,8 x .
27) ►Problème 2°)
J’achète des pommes à 1,53 € le kilogramme
; quelle sera la relation mathématique à
utiliser ?
Solution :
27a) si « y »
est le prix à payer et « x » le nombre de kg ,quel sera est le coefficient
de proportionnalité ? 1,53 .
27b) Donner la forme de
l’équation de ce que je dois payer je dois payer : y = 1,53 x
Applications :
27c) -si je prend 4,5 kg
; je payerai y = 1,53 fois
4,5 ; soit 6,885 €
27d ) -si je prend 1, 350 kg ; je payerai y = 1,53 fois
1,350 ; soit 2,0655 €
2 7 e ) Conclusion : Avec la relation y = 1,53 x je peux
calculer la somme à payer quelque soit la masse;
je multiplie la valeur de cette masse
par 1,53 .
28 °) ►Problème
n° 3
J’ai payé 7,2 € pour des pommes vendues 0,8 € au kg . Quelle
est la masse de pommes achetées ?
28a) On sait
que la relation à utiliser est
y = 0,8 x
28b) On connaît « y
= 7,2 » , on peut écrire 7,2 =
0,8
x
|
Pour calculer
« x » on transforme l’équation : |
|
On simplifie pour obtenir : ![]()
28c) Donc x = 7,2 ¸ 0,8 ; soit
x = 9
28 d)
conclusion : la masse de pommes achetées est de 9 kg.
Série 2 :
Autre méthode de résolution d’un problème sur les proportionnalités :
on raisonne en passant
par le tableau de proportionnalité.
29 ) Problème n° 4 : J’ai payé 7,2 €
pour 10 kg pommes combien
paierai-je pour 4 kg ?
(on a
établi le tableau suivant)
|
Nombre de kg |
10 |
4 |
|
Prix payé |
7,2 |
( x
) |
Calcul : On fera le produit en croix :
10 ´ ( x )
= 7,2 ´
4 ; on transforme : ( x) =
( 7,2 ´ 4 ) ¸ 10 ; x = 2,88
Conclusion :
le prix à payer pour 4 kg est de 2,88 €.
+Première approche : nous
avons vu précédemment que nous pouvions
mettre dans un tableau des valeurs
calculées.
30°) Problème n° 5 : J’ai payé
pour des pommes vendues 2 € au kg . Combien paierai-je si j’achète une masse
de 1,5 kg ; 4,3 kg et 9,600 kg
; pommes achetées ?
30a) Construire le tableau de proportionnalité
|
´ 2 |
¯ |
1,5 |
4,3 |
9,6 |
|
¸2 |
|
3 |
8,6 |
19,2 |
|
+Deuxième approche : théorique
31°) Problème n°6 :
J’ achète des pommes vendues 2 € au kg . Combien
paierai-je si j’ achète une masse
« quelconque » ( notée par la lettre « x » ) de
pommes achetées ?
On demande d ’
établir l’équation et de construire un tableau ou l’on peut connaître les
prix à payer pour des sacs contenant 1,5 ; 2 ;
2,5 ; 3 ; 4 et 5 ( kilos
achetés)
Solution :
31a )On pose :
« x » pour les kilos achetés ; « y » pour le prix à payer ;
 31b)
On en déduit l’équation « y = 2 x »
31b)
On en déduit l’équation « y = 2 x »
31c) Construire un
tableau de proportionnalité ,
précisez !! :
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|


31d) construire un
tableau . Placer les valeurs 1,5 ; 2 ; 2,5 ; 3 ;
4 et 5 on sait que : y = 2 x
compléter le tableau.
|
|
x |
1,5 |
2 |
2,5 |
3 |
4 |
5 |
|
|
y |
3 |
4 |
5 |
6 |
8 |
10 |
|
on
Recherche le coefficient de
proportionnalité |
La recherche du
coefficient de proportionnalité est un autre
moyen de traiter les problèmes de proportionnalité.
32 °) Problème n° 7 : j’achète 9 kg de pommes pour 7,2
€ ; une offre
promotionnelle propose un lot de 3 kg de ces mêmes pommes à 2,99 €.
Y a - t-il un rapport de proportionnalité ? expliquez comment on doit procéder .
Solution :
32 a) Calculs : Pour le savoir on effectuera les deux calculs suivants
( 7,2 : 9 et 2,55 : 3 ) et puis on comparera le résultat de ces calculs : 7,2 : 9 = 0,8 ; 2,55 : 3 = 0,85 ;
0,8 et 0,85
ne sont pas égaux !
32b)
Conclusion : Il n’y a pas de
proportionnalité parce que l’on a pas obtenu le même quotient.
|
VII. autre activité : Faire
la Représentation graphique d' une
proportion |
33°) compléter la phrase : La représentation graphique d'une situation
de proportionnalité est une droite qui passe par l'origine .( O ) du repère cartésien.
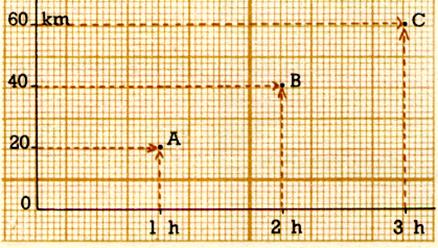
34°) Exemple
N°8 : Un cycliste se déplace à la vitesse moyenne de 20 km par
heure ( 20 km/h ou 20 km.h-1 ).Déterminer
l’équation « y » distance parcourue(km) en fonction de
« x » durée du parcours(h) ; construire un tableau de proportionnalité avec x = 1 h ; 2h et 3 h ; Tracer
la droite dans un repère cartésien.
34a) donner l’équation algébrique : L'équation
algébrique est y = 20 x
34b)
compléter : Avec " y " représente : la distance parcourue,
"x" représente la durée en
heure.

34c) compléter le
tableau :
|
Durée en h. |
1 |
2 |
3 |
|
Distance parcourue |
20 |
40 |
60 |
34 d) Compléter les
colonnes par une lettre majuscule.
Pour la représentation graphique ( on reprend le
tableau précédent on nomme les colonnes )
|
Points ® |
A |
B |
C |
|
Durée en h. |
1 |
2 |
3 |
|
Distance parcourue |
20 |
40 |
60 |
34 e) Tracer le
repère sur « x » 1h = 2
cm ; sur « y » 20 km = 1
cm ) ;
Donner les valeurs
des couples de points et puis les
placer dans le repère .
les points
A ( 1 ; 20)
; B ( 2 ; 40 ) ;
C ( 3 ;60 )
|
La
représentation graphique est une droite ( ensemble de points) |
|
|
VIII. problème résolu ; Activités |
|
35°) Rechercher
un complément d'informations à la lecture de la représentation graphique, et interpréter certains
événements :
|
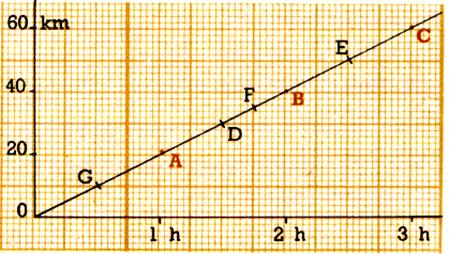
Soit la représentation graphique ci- contre. « Soit un cycliste qui quitte un lieu en un
point O » . |
|
35a) Compléter le tableau ci - dessous :
|
|
? |
G |
? |
D |
F |
? |
E |
? |
|
Durée en h. |
0 |
|
1 |
|
|
2 |
|
3 |
|
Distance parcourue |
0 |
|
20 |
|
|
40 |
|
60 |
2°) Quel commentaire peut - on faire sur
les points : G :
D ; F et E ?.
Solution :a) Après avoir remplir le tableau :
|
|
O |
G |
A |
D |
F |
B |
E |
C |
|
Durée en h. |
0 |
0,5 |
1 |
1,30 |
1,75 |
2 |
2,50 |
3 |
|
Distance parcourue |
0 |
10 |
20 |
30 |
35 |
40 |
50 |
60 |
35 b ) commentez ce qui se passe au point « G » , au point « D » au point « F » ; « E »:
On peut faire
les commentaires suivants :
au point "G" il met
0,5h pour parcourir 10 km
au point "D" il
parcourt 30 km en 1,5 h
au point "F" en 1,75
h ( 1 .![]() h ou 1 h 45 min) il a
parcouru 30 km
h ou 1 h 45 min) il a
parcouru 30 km
au point "E" il a parcouru
50 km au bout de 2,5 h ( 2h 30 mn )
|
Pré requis :
repérage et les calculs |
Revoir ce dessus pour ce qui est du vocabulaire
employé. !!!!!!
Dans ce chapitre
1°) il faut
savoir : compléter et utiliser un tableau de proportionnalité , et ;
2°) il faut savoir
déterminer , représenter et utiliser l’application linéaire liée à une situation
de proportionnalité .
36°) Application
linéaire :
36
a) Que désigne « k »
(quelle est sa nature ?):
«
k » est le coefficient de
proportionnalité , c’ est un nombre non nul (
¹ 0)
36b) L’ ’application
linéaire de coefficient « k » fait correspondre à chaque nombre
« x » le nombre « y »
, traduire en une équation mathématique :
on notera le modèle k ´ x = y
soit y = k x ,
36 c) compléter la phrase : on dira
que le produit de « k x » est l’image de « x » par l’application linéaire
de coefficient « k » . On dira donc
que « x à pour
image k x »
36d) Par quel symbole
remplace - t- on l’expression « à
pour image » ?
On remplace
l’expression « à pour image » par le
dessin : ![]() ( flèche orientée de vers la droite, la flèche aura un talon (trait
vertical lié) )
( flèche orientée de vers la droite, la flèche aura un talon (trait
vertical lié) )
36 e) Traduire en
écriture symbolique : « x à pour image k x
» : on notera cette phrase par l’écriture symbolique :
x ![]() k x
k x
36
f ) Compléter la phrase : « y » est le produit de k x ( lire
« k » fois « x » )
36 g) Si l’application linéaire s’appelle « f » et si « y » est l’image de
« x » ;
traduire en écriture symbolique : y = f (x)
36 h ) On lira que : chaque valeur de « y » est obtenu en fonction
de la valeur de « x » .
37°) Application linéaire liée à une situation
de proportionnalité .
37 a) on donne : x ![]() -3,5
x est associé à ce tableau de proportionnalité ;
compléter le tableau
-3,5
x est associé à ce tableau de proportionnalité ;
compléter le tableau
|
´
-3,5 ¯ |
x |
- 3 |
- |
0,4 |
1 |
2 |
|
|
y |
+10,5 |
+1 |
-1,4 |
-3,5 |
-7 |
|
37 b) Représentation
graphique . ( voir chapitre ci dessus : 6°
)Représentation graphique d' une
proportion )
Compléter la
phrase : La représentation
graphique de l’application linéaire de coefficient « k » est la droite d’équation y
= k x
37 c) par quels points particuliers passe - t-
elle ? Elle
passe par les
points particuliers :
point « O » (
0 ;0) et par le point
« A » ( 1 ; k )
38°)
Coefficient :
soit l’application linéaire f telle que
f ( 2) = (
-13)
38 a) calculer sont « k » : à pour
coefficient ![]() car
car ![]()
38 b) généraliser : l’application
linéaire f telle que f(x) = k x
à pour coefficient : « k » = ![]()
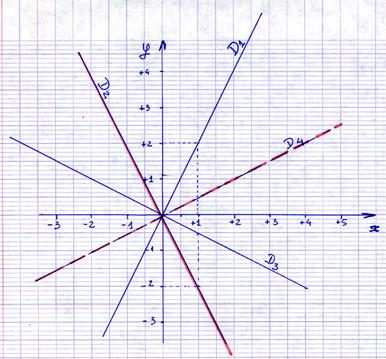
39°) Exemple de
représentations graphiques :
Que peut -on dire des droites sur le dessin ? Complétez
les phrases.
|
39 a) La représentation graphique d’une fonction
linéaire est une droite passant par « O ». 39 b) D1 ; D2 ; D3 ;
D4 sont des droites passant par « O » 39 c) ces droites sont les représentantes d’une
fonction …linéaire. 39 d) Quel est le signe de
« k » pour chaque ? D1 : k
positif ; D2 k
négatif; D3 k
négatif D4 k
positif |
|
Ceci
termine la découverte du document , vous devez demander des précisions si les
réponses ne vous ont pas paru « évidente ».