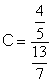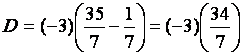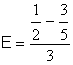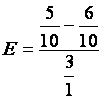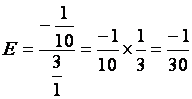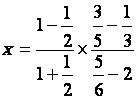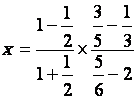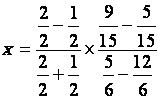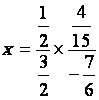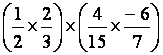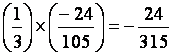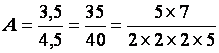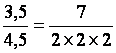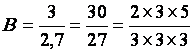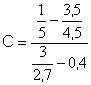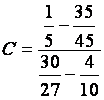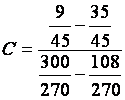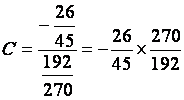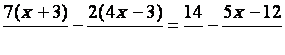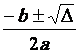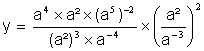Site warmaths Pour Aide et Formation Individualisée

PAGE D ‘ENTREE

ICI pour aller PROGRAMME de seconde.

INFORMATIONS PEDAGOGIQUES :

Module 1

Matière : MATHS

« TRAVAUX »

TITRE : corrigé : L’ ENSEMBLE R des réels ( niveau Seconde)

Classe : Seconde :NIVEAU : IV

OBJECTIFS : - Savoir calculer dans R

I ) Pré requis: (pour remédiation ou mise à niveau)

Calcul numérique avec des nombres entiers et décimaux.

i9

Calcul numérique avec les décimaux relatifs

:i

II ) ENVIRONNEMENT du dossier :

Index : retour vers warmaths.

Dossier précédent :

Dossier suivant :

Info :

III ) INFORMATIONS «  formation leçon » :

Test

COURS : voir à chaque cas

Travaux auto - formation.

Corrigé des travaux auto - formation.

Contrôle

évaluation

INTERDISCIPLINARITE

Corrigé Contrôle

Corrigé évaluation

Chapitres :

Info +voir les calculs avec des fractions++

Série des Exercices 1 , calculer les réels suivants :

;

; ;

;

; après simplification (forme irréductible) autre forme décimale B = 1,3

Solutions : S1 : soit développer ; S2 : soit faire le calcul dans les parenthèses : S1 : = = S2 : = ou D =

;

Série des Exercices 2 :calculer

; = = =

Info plus.

Série des Exercices 3, écrire sous la forme d’une fraction irréductible chacun des rationnels suivants

; le PGCD = 5 ;  ;

;  ;

= = = =  ;

Série 4 : Résoudre dans R les équations suivantes

InfO ++++

1°) 6 x - 2 [ x - 3 ( x + 1) ] = 0,5

· 6 x - 2 [ x - 3 ( x + 1) ] - 0,5 = 0 · 6 x - 2 [ x - 3 x -3 ) ] - 0,5 = 0 · 6 x - 2 [ 2 x - 6 ) ] - 0,5 = 0 ; · 6 x - 4 x +12 - 0,5 = 0 ; · 2x +11,5 = 0 ; · 2 x = - 11,5 ; x =  ; x = 5,75

2°)

· ; · ·  ; · 7 x +21 - 8x +6 = 14 – 5x +12 ; · - x + 27 = 26 – 5x · 4 x = -1 ; · x = - 0,25

3°)

· · · · 30 ( 2 x + 2) – 40(x-1) – 36 = 30 x · 60 x + 60 – 40 x + 40 – 36 = 30 x · 60 x + 60 – 40 x + 40 – 36 - 30 x = 0 · 60 x + 100 – 40 x – 36 - 30 x = 0 - 10 x + 54 = 0 · = 10 x · x = · x = 5,4

Série 5

Résoudre dans R les équations suivantes.

Info ++

1°) x ( x -2) = 3 ( x - 2)

x( x -2 ) - 3( x – 2 ) = 0 ; ( x-2)( x-3)=0 si un des facteurs est nul ; le produit est nul : si ( x - 2) = 0 ; sol x = 2 ; si ( x-3)= 0 alors x = 3. Solutions : «  x = 2 ou 3 »

Info °°°i

2°) ( 3 x -5) ² = ( 2x - 3)²

· ( 3 x -5) ( 3 x -5) = ( 2x - 3) ( 2x - 3) · 9 x² - 15 x – 15 x +25 = 4 x² - 6 x - 6 x + 9 · 9 x² - 30 x + 25 = 4 x² -12 x + 9 · 5 x² - 18 x + 16 = 0 · calcul du « delta » = b² - 4 ac ; ( - 18 )² - 4 ( 5 fois 16) = 324 - 320 = 4 : racine de delta = 2 cas : b² - 4 ac > 0 «x » a deux valeurs distinctes  ( que l’on nome « x prime » et « x seconde ») x’ :et x’’ = S1 = = 2 ; S2 = = 1 ,6 En conclusion : S = 2 et 1,6

3°) 4 x^3 + x = 4 x²

4 x^3 + x - 4 x² = 0 x ( 4 x² - 4 x +1) =0 on remarque : ( 4 x² - 4 x +1) est de la forme (‘A + B)² soit ( 2x + 1 ) ² d’où S = 0 et – 0,5

Série 6 : info +++

Soit « a », « b », « a’ » et « b’ » des réels , « a’ » et « b’ » non nuls ; démontrer que équivaut à ab’ = a’b En effet , soit ; réduisant les deux rapports au même dénominateur , on obtient : ; d’où «  ab’ = a’ b »

Résoudre dans R l’ équation :

· Produit en croix : ( x – 5 ) ( x – 7 ) = ( x + 1 ) ( x + 3 ) · x² - 7 x – 5 x + 35 = x ² + 3 x + x + 3 · x² - 12 x + 35 = x ² + 4 x + 3 · x² - 12 x + 35 - x ² - 4 x - 3 = 0 · 0 x² - 16 x + 32 = 0 · 16 x = 32 · · «  x = 2 »

Série 7

1°) Calculer :

Info +++

2^-1 =

=

2 ^3 =

2 x 2 x 2 = 8

2^-3=

= = 0,125

( -2) ^3 =

( - 2 ) ( - 2 ) ( - 2 ) = ( - 8 )

= = = 0,125

( -2) ^7 =

( - 128 )

2°) soit « a » un réel non nul, simplifier l’expression :

Série 8

Mettre chacun des nombres suivants sous la forme : 2 ^a ´ 3^b ´ 5^c , où « a » , « b » , « c » sont des entiers.

A = 2^3 ´ 3² ´ 4^3 ´5^6 ´ 6^5´ 10^9

B = 4860

C = 49 200

Série 9

Ecrire sous forme décimale chacun des nombres suivants, puis vérifier le résultat à la calculatrice.

A = 10^4 + 10^2 + 10 + 10^- 2

Série 10

Notation scientifique

Info.+++

Ecrire en notation scientifique chacun des nombres :

X= 573 000

Z = 35,73 ´ 10 ^11

Série 11

ENCADREMENTS

Info +++

A)

Sachant que : 2,237 < a < 2,238 , trouver le meilleur encadrement de chacun des réels suivants :

2a

-a

3 - a

B)

Encadrement d’une somme.

1°)Montrer que si « a » , « b » , « c » et « d » sont des réels tels que a £ b et c£ d , alors a + c £ b +d

2°) Application : On donne : 2,49 £ A £ 2,50 et 3,15 £ B £ 3,16 ; encadrer A + B et A - B

C)

Encadrement d’un produit.

1°) Montrer que si « a » , « b » , « c » et « d » sont des réels strictement positifs tels que : a £ b et c£ d , alors a c £ b d

2° Application : On donne : 2,49 £ A £ 2,50 et 3,15 £ B £ 3,16 ; encadrer A B par deux décimaux comportant deux chiffres après la virgule.

Série 12

Intervalles

A)

Dans chacun des cas suivants , représenter sur une droite graduée les intervalles donnés , puis déterminer leur intersection et leur réunion :

1° )

A = ]- 5 ; 4 ] et B = [ 1 ;7 [

2°)

C = ]- ¥ ; 4 ] et D = ] 0 ; + ¥ [

3°)

E = ] - p ; p [ et

4°)

G = ] - ¥ ; [ et H = [  ; + ¥ [

B)

Résoudre , dans R , chacune des inéquations et le système suivant ( donner l’ensemble des solutions sous forme d’intervalle)

1°) 2x - 3 ³ 0

2°)

3°)

Série 13

Valeur absolue.

Ecrire plus simplement , c’est à dire sans les barres de valeur absolue, chacun des réels suivants :

Ecrire à l’aide de la distance, puis résoudre dans R chacune des équations suivantes :

1°)

2°)

3°)

4°)

5°)

Ecrire à l’aide de la distance, puis résoudre dans R chacune des inéquations suivantes (donner l’ensemble des solutions sous forme d’intervalle ou de réunion d’intervalles).

1°) a) b)

2°) a ) b)

Procéder comme dans l’exercice précédent pour résoudre dans R

1°)

2°)

3°)

Série14

Calculs avec des radicaux :

Sans utiliser de calculatrice, écrire chacun des réels suivants sous une forme simple.

Ecrire les réels suivants sous une forme plus simple, sans dénominateur ou avec un dénominateur entier :