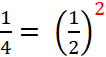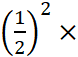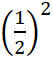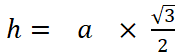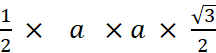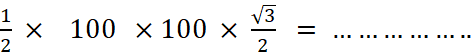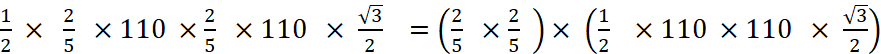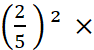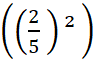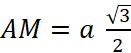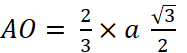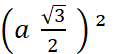Programme 3^ème
			Classe P3
Pré requis:
Représentation des solides.			( pas encore de corrigé)
Notion : sur les « volumes »

ENVIRONNEMENT du dossier:

Index : « warmaths.fr »

Objectif précédent : · Les solides.. · Les sections planes. · La pyramide (définitions…)

Objectif suivant : 1°) les calculs 2°) Le tronc de pyramide . 3°) Les polyèdres

· Info sur : les volumes · Sommaire sur « les volumes ».

3^ème .	DOSSIER : Fiches sur La PYRAMIDE .
	Fiche n° 1 : Reconnaitre « 4 » modèles de pyramides.
	Fiche n°2 : Section d’une pyramide par un plan parallèle à la base.
	Fiche n° 3 : Une autre propriété des plans parallèles.
	Fiche n° 4 : Calculs dans une pyramide .
	Fiche n° 5 : Section d’un tétraèdre régulier par un plan parallèle à la base.
	Fiche n° 6 : Arêtes opposées d’un tétraèdre régulier .
	Fiche 7 : Calcul de la hauteur d’un tétraèdre régulier

Fiches sur La PYRAMIDE
Voici une représentation en perspective cavalière de 4 pyramides.
Fiche 1 : « 4 » modèles de pyramides.	« @ perspectives »
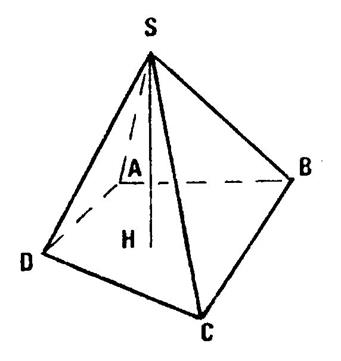
Pyramide n°1 : C’est une pyramide quelconque . « S » est son sommet. Le polygone quelconque « ABCD » est sa base. [ SH ] est sa hauteur . ( remarquez que la hauteur est perpendiculaire au plan de la base). [ SA ], [ SB ], [ SC ], [ SD], sont ses arêtes latérales. Les triangles « SAB » , « SBC », « SCD » , SDA » sont des faces latérales. Dans TOUTE pyramide, les faces latérales sont toujours des triangles.
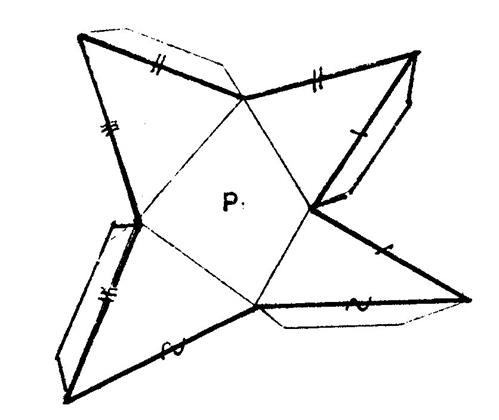
On vous demande de construire la pyramide quelconque . Pour cela, prenez la feuille en cliquant ci-contre «  Pyramide n°1 » Pour cela , prenez la fiche et complétez la figure du haut de telle sorte que le dessin obtenu ressemble au dessin ci-dessous. Les segments de même longueur sont repérés de la même façon . Découpez – le et fabriquez la pyramide.
Fiche : Patron de la pyramide n°1 (quelconque) On vous demande de construire
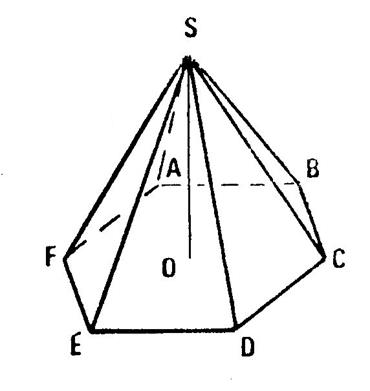
Pyramide n°2 : C’est une pyramide dite « régulière ». Une pyramide régulière est une pyramide dont la base est un polygone régulier et dont la hauteur passe par le centre du cercle circonscrit au polygone de base. Dans le cas de la pyramide n°2 , ce polygone est un …hexagone………régulier . Démontrez oralement que les arêtes latérales ont même longueur et que les faces latérales sont des triangles ……isocèles …...
Vous devez construire la pyramide n°2 . Pour cela , complétez le dessin (cliquez ) ) pour d’obtenir le patron de la pyramide n°2. N’oubliez pas les languettes . Découpez le patron et fabriquez la pyramide.
Pyramide n°3 :
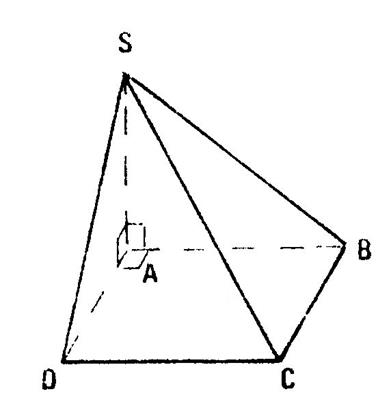
Cette pyramide est une pyramide dans laquelle la hauteur est confondue avec une arête et dont la base est un rectangle. Vous allez construire la pyramide n°3 . Pour cela imprimer la fiche (cliquez ici ) . Le patron y est dessiné , mais ce n’est pas celui de « n°3 » . Pour obtenir le patron de la « N°3 » , vous allez reproduire ce dessin à l’échelle ½ . On a déjà placé en bas ( à gauche) le dessin du rectangle de base. N’oubliez pas les languettes . Découpez votre dessin et fabriquez la pyramide n°3.
Pyramide n°4 :
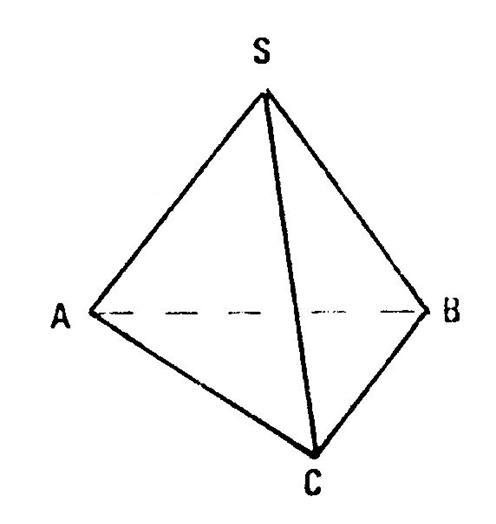
La pyramide n°4 est un tétraèdre régulier . Un tétraèdre est une pyramide dont la base est un triangle. Les 4 faces sont alors des triangles et chacune d’elle peut être prise comme base. Un tétraèdre régulier est une pyramide dont les arêtes ont même longueur . Les 4 faces sont donc des triangles …………………………. Vous allez construire la pyramide n°4 . Pour cela prenez la fiche ci-dessous. Le patron d’une pyramide y est dessiné, mais ce n’est pas celui de la pyramide n°4 . Pour obtenir le patron de la pyramide n°4 (cliquez ici ) , reproduisez ( en haut à gauche ) ce dessin à l’échelle. N’oubliez pas les languettes. Découpez votre dessin et fabriquez la pyramide n°4.
Fiche pyramide n°4. Image
Fiche n°2 : Section d’une pyramide par un plan parallèle à la base.	@ info }}}
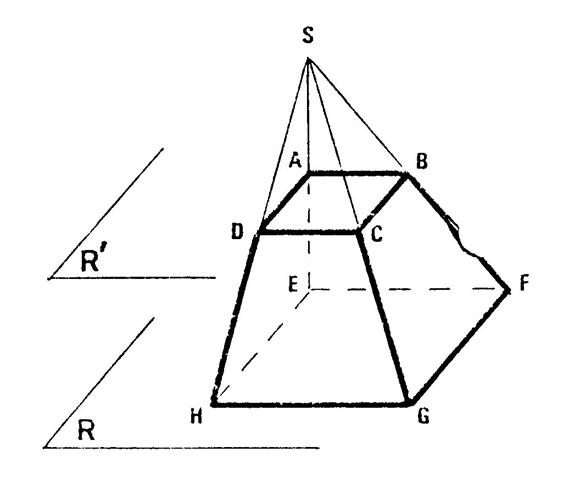
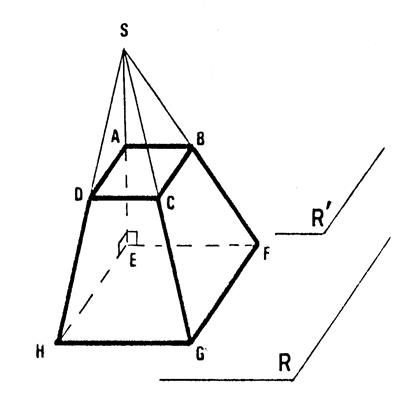
Voici , ci-contre , le dessin en perspective cavalière d’un tronc de pyramide. Ce solide a été obtenu en coupant la pyramide « SEFCH » par un plan strictement parallèle à la base. Appelons « R » le plan de base et « R’ » le plan parallèle. Appelons « Q » le plan de la face « SHC » de la pyramide. « Q » coupe « R’ » ( il est possible de le démontrer). L’intersection de « R » et de « Q » est la droite « (HG) ». L’intersection de « R’ » et de « Q » est la droite ……( DC )… Apparemment , (HG) et ( DC) sont …parallèles …. C’est ce que nous allons démontrer.
( HG ) et ( DC) sont situées dans le plan « Q » . Dans ce plan , si elles ne sont pas parallèles alors elles sont sécantes .. Puisque ( HG ) est dans le plan « R » , et ( DC ) dans le plan « R’ » alors leur point d’intersection est à la fois dans et plan « R » et dans « R’ ». Or , « R » et « R’ » sont strictement parallèles , ils n’ont donc pas de point commun. Donc les droites ( RC ) et ( DC ) ne peuvent être sécants , elles sont donc parallèles .
Théorème : Si deux plans sont parallèles et si un plan coupe l’un alors il coupe l’autre et les deux droites d’intersections sont parallèles.
Fabrication d’un tronc de pyramide.
Prenez la page ci-dessous ,le patron d’une pyramide « P » y est dessiné. Vous allez modifier ce dessin afin d’obtenir le patron d’un tronc de pyramide. Le plan « R’ » parallèle à la base coupera les arêtes de la pyramide « P » en leur milieu. On appellera « ABCDEFGH » ce tronc de pyramide ( comme sur le dessin ci-dessus)
On a déjà placé le point « A » . Placez « D » , tracez (AD ). D’après le théorème précédent , (AD) doit être parallèle à ………. Ce qui est le cas puisque (AD) passe par les ……….. de côtés du triangle « SEH ». Dessinez l’intersection du plan « R’ » avec les autres faces de la pyramide. L’intersection de la pyramide « P » avec le plan « R’ » est le quadrilatère « ABCD ». Puisque « ABCD » a ses côtés respectivement parallèles à ceux de « EFGH » , et comme « EFGH » est un rectangle , alors « ABCD »est un …………….. N’oubliez pas de le dessiner où il faut et pensez aux languettes d’assemblage. Découpez le patron ainsi obtenu et fabriquez le tronc de pyramide.
Comparaison des pyramide « P » et « P-n°3 »
Le dessin à l’échelle ½ du patron « P » nous a donné le patron de « P n°3 » Puisque l’on a coupé la pyramide « P » par un plan passant par le milieu de ses arêtes latérales , alors la pyramide enlevée n’est autre que « P n°3 ». En plaçant convenablement « P n°3 » sur le tronc de pyramide , vous obtenez la pyramide « P ».
Puisque « A » , « B » , « C » , « D » sont les milieux des arêtes, alors : « SA = …..SE » ; « SB = …..SF » ; « SC = …..SG » ; « SD = …..SH » ; Vous en déduisez : * « AB = …..EF » ; « BC = …..FG » ; « CD= …..HG » ; « DA= …..HE » ; La pyramide "P n°3" , apparaît comme une réduction de « P » , le coefficient de réduction étant égal à …………………………..
Comparaison des aires.
Sachant que “EFGH” est un rectangle dont les dimensions sont « 80 mm » et « 60 mm ». Vous en déduisez que les dimensions de « ABCD » sont ………mm et …….mm. ( aire EFGH) = 80 mm 60 mm= ……………….mm² . ( aire ABCD ) = ……… mm ……….. mm= ……………….mm² . On peut écrire : ( aire EFGH) = ……………… ( aire ABCD ) Ou encore : ( aire ABCD ) = ……………… ( aire EFGH ) et vous remarquez que : ( aire ABCD ) = AB BC = ( EF) ( FG) = ( ) ( ) ( EF FG) = ( aire EFGH) Il en serait de même pour les faces latérales , on dit alors : Si les longueurs sont multipliées par ( ) , alors les aires sont multipliés par .
Fiche 3 : Une autre propriété des plans parallèles.
Sur le tronc de pyramide que vous venez de fabriquer , écrivez les noms des sommets : A ; B ; C ; D ; E ; F ; G : H. · Considérons la droite support de l’arête [ EA ]. Elle est perpendiculaire à ( EF ) et à (EH). Elle est donc perpendiculaire au plan « R » de la base. ( voir théorème de la leçon … « Pythagore »., fiche n° 7..) ..) · Dans le plan (SEF) , puisque « R » et « R’ » sont parallèles, alors les droites (EF) et (AB) sont ………………………….et comme (EA) est perpendiculaire à (EF), alors ( EA )est perpendiculaire à ……………………… · Dans le plan ( SEH) , puisque « R » et « R’ » sont parallèles ,alors les droites ( EH ) et (AD) sont ………………….et comme ( EA )est perpendiculaire à (EH) alors ( EA ) est perpendiculaire à ……………………………
· ( EA ) étant perpendiculaire à deux droites sécantes (AB) et ( AD ) du plan « R’ »alors ( EA ) est ………………………………………….au plan « R’ » ( grâce au théorème de la leçon … « Pythagore »., fiche n° 7..)
Théorème : Si deux plans sont parallèles et si une droite est perpendiculaire à l’un, alors elle est perpendiculaire à l’autre.
Fiche 4 : Calculs dans une pyramide .
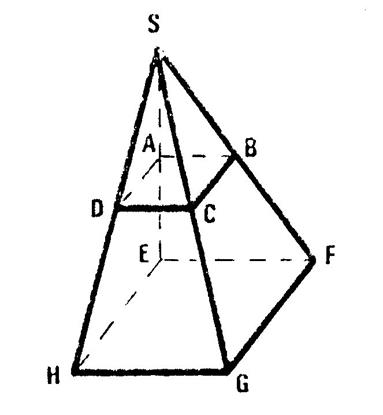
Reprenons la pyramide « P ». (c’est le tronc de pyramide surmonté de « P n°3 ».) Le support de l’arête [ SE ] est perpendiculaire à la base donc | SE] est ………..pour la pyramide « P ». Sa base « EFGH » est un rectangle. SE = 100 mm ; EF = 60 mm ; EH = 80 mm Etudions les faces et calculons la longueur des arêtes . Face « SEF » :  (SE) est perpendiculaire à ( EF) donc le triangle « SEH » …………… Calculez "SF". ( Donnez la  valeur exacte simplifiée et une valeur approchée à 1mm près.)
Face « SEH » : ( SE ) est perpendiculaire à ….. donc le triangle « SEH » ………………………… Calculez « SH » . ( Donnez la  valeur exacte simplifiée et une valeur approchée à 1mm près.)
Face « SHG » . Démontrons que « SHG » est un triangle rectangle en « H ». ( SE ) est perpendiculaire au plan de la base donc à toutes droites de ce plan. Donc (SE) est perpendiculaire à ( HG ) et comme « EFGH » est un rectangle , alors ( EH ) est perpendiculaire à ( HG ). (HG ) est alors perpendiculaire à deux droites sécantes ( SE ) et ( EH ) du plan ( SEH) donc grâce au théorème « théorème de la leçon … « Pythagore »., fiche n° 7. » , ( HG ) est perpendiculaire au plan ( SEH) donc ( HG ) est perpendiculaire à toutes les droites de ce plan donc ( HG ) est perpendiculaire à ( SH ) . Donc le triangle « SHG » est rectangle en « H ». · Calculez « SG ».
Face «  SGF » : Démontrez que « SGF » est un triangle rectangle et retrouvez la valeur de « SG ». ( il existe un autre triangle rectangle permettant de calculer « SG » . Lequel ? …………………………….)
Fiche 5 : Section d’un tétraèdre régulier par un plan parallèle à la base.
La page ci-dessous , vous propose le patron d’un tétraèdre régulier « T » y est dessiné . Vous allez modifier ce dessin afin d’obtenir le patron d’un tronc de pyramide. Le plan « R’ » parallèle au plan « R » de la base coupera l’arête [ SD ] en un point « A » tel que .
Puisque « R ‘» est parallèle à « R » , grâce au théorème de la fiche 2 , on doit avoir : ( AB ) // ( DE ) , ( BC ) // ……. , ( CA ) // ………. Dans le triangle « SDE », puisque ( AB ) est parallèle à ( DE ) , grâce au théorème de Thalès : on a Or donc SB = ……..SE et AB = ……DE. On prouverait de même que les triangles « SEF » et « SFD » que : SC = ...........……………., BC = …………………….., CA = …………………
« SDEF » est un tétraèdre régulier . SD = SE = SF = DE = EF = FD = 10 mm. Donc : SA ….SB … SC ……….AB ……………BC ………..CA = ……………………mm. La pyramide « SABC » n’est autre que la pyramide « P n°4 » « P n°4 » apparaît comme une réduction de « T » . Le coefficient de réduction étant égal à : ……………………………………..
· Vous pouvez alors terminer le dessin du patron du tronc de pyramide. L’intersection de la pyramide et du plan « R’ » est un triangle ……………………………………. N’oubliez pas de la faire figurer sur le patron et pensez aux languettes d’assemblage. Découpez le patron ainsi obtenu et fabriquez le tronc de pyramide. En plaçant convenablement « P n°4 », sur le tronc de pyramide , vous obtenez la pyramide « T ».
Comparaison des aires.
Les faces du tétraèdre « T » sont des triangles équilatéraux dont le côté mesure 110 mm. Les faces du tétraèdre « P n°4 » sont des triangles équilatéraux dont le côté mesure ………. mm. Pour tout triangle de côté « a » et de hauteur « h » , l’aire est égale à . Dans le cas de triangle équilatéral , «  » donc l’aire est égale à ( L’aire d’une face de « T » ) = ( L’aire d’une face de « P n°4 » ) = Or , , on peut donc écrire : ( L’aire d’une face de « P n°4 » ) = ( L’aire d’une face de « P n°4 » ) =( L’aire d’une face de « T » ) . On peut dire : Si les longueurs sont multipliées par , alors les aires sont multipliées par Ce qui est vrai pour des pyramides l’est aussi pour tous les autres objets géométriques.
Théorème . Dans l’agrandissement ou la réduction d’un objet géométrique , si les longueurs sont multipliées par un nombre « k » , alors les aires sont multipliée par « k² ».
Fiche 6 : Arêtes opposées d’un tétraèdre régulier .
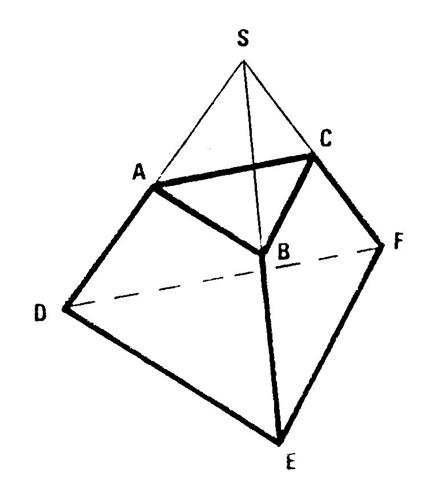
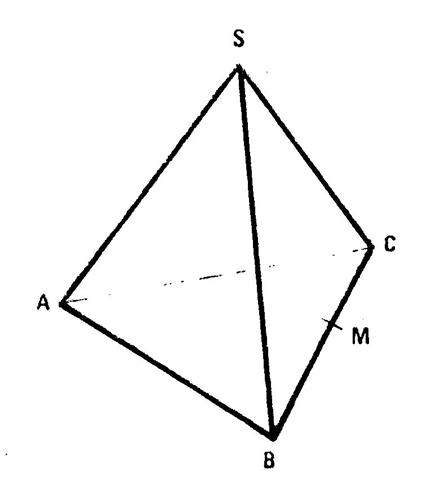
Reprenons le tétraèdre régulier « P4 ». apparemment , ( SA ) et ( BC sont ……………………………. C’est ce que nous allons démontrer. Appelons « M » le milieu de [ BC]. Dans le triangle « ABC » , [ AM ] est une médiane. Puisque « ABC » est un triangle équilatéral , [AM] est aussi hauteur donc ( AM ) est ……………………………………à ( BC ). Dans le triangle « SBC » , on démontre de même que ( SM ) est ………………….à ( BC ) . A vous de continuer.
Fiche 7 : Calcul de la hauteur d’un tétraèdre régulier
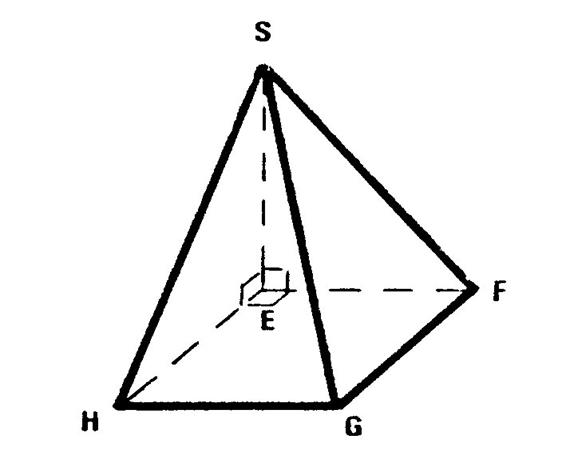
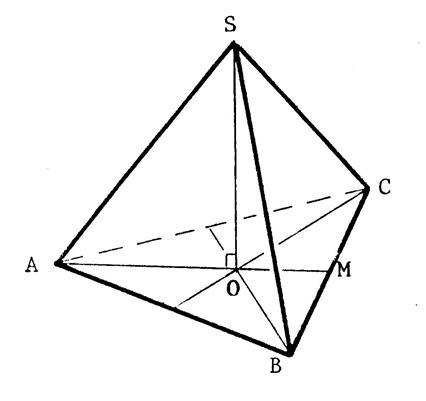
« SABC » est un tétraèdre régulier dont la longueur des côtés est « a ». « O » est le centre du triangle équilatéral « ABC » . [ SO ] est hauteur. Calculons SO . ( SO ) est perpendiculaire au plan ( ABC ) donc ( SO ) est …………………….à ( AO ) donc le triangle « OAS » est ………………………………………. Nous allons calculer SO . dans ce triangle en utilisant le te théorème de Pythagore. Pour cela , calculons AO . ( AO) coupe (BC) en « M ». Puisque « ABC » est un triangle équilatéral , [ AM ] est à la fois hauteur et médiane.
Puisque [ AM ] est hauteur du triangle « ABC », alors  ; (voir théorème de la leçon … « Pythagore »., fiche n° 5. ) « O » étant point d’intersection des médianes , alors ( voir le cours de 4^ème ) Donc et après simplification AO = ………………………………….. Dans le triangle « OAS » , SO² = SA² - ………………..= a² - = ……………………………= …………… ; D’où c'est-à-dire SO = …………….