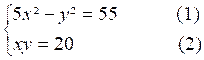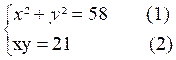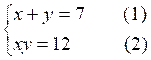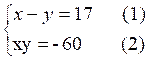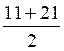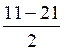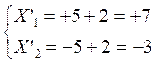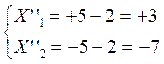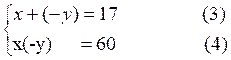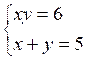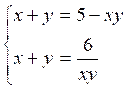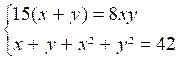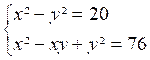Systèmes du second degré

DOC. : Professeur ; Formateur

DOC : Formation Individualisée

DOC : Elève.

 

DOSSIER  N°

Matière : MATHEMATIQUE

Information « TRAVAUX »

Cliquer sur  le mot !.

INFORMATIONS PEDAGOGIQUES :

Formation :     NIVEAU  IV :

OBJECTIFS :- Savoir résoudre  l’équation du second degré  avec S et P                    

I ) Pré requis:

 

1-

Les théorèmes  sur les égalités.

 

2-

Savoir résoudre une équation de la forme a x² + b x + c = 0

 

 

II ) ENVIRONNEMENT du dossier :

 

Index  warmaths

 

1°) Dossier étude du second degré à une inconnue  :

 

2°) Somme et produit  dans le second degré

 

Dossier suivant :

 

- vers le Niveau IV

 

- Les fonctions de la forme : y = a x² + b x + c

Info :

Info :  Retour vers la liste des cours sur le second degré « équations »

Tableau synoptique  :i

 

-        Liste des cours en algébre.

 

 

 

 

 

LE SECOND DEGRE : SYSTEMES D’ EQUATIONS.

 

 

 

 

 

Chapitres :

i9  

Exemple 1 (utilisation de la méthode par substitution.) forme :   

 

 

:i

i9  

Exemple 2 : forme  

 

:i

   

 

:i

i9  

Exemple 3 : forme     

 

:i

i9  

Exemple 4 : forme   

 

 

:i

 

IV)   INFORMATIONS  «  formation leçon » :

 

Test

 Boule verte

COURS  Boule verte

Travaux  auto - formation.

 

Corrigé des travaux  auto - formation.

Contrôle Boule verte

évaluation Boule verte

Boule verteINTERDISCIPLINARITE

Corrigé Contrôle

Corrigé

 évaluation

 

V )   DEVOIRS  ( écrits):

 Devoir diagnostique L tests.

 Devoir  Auto  - formatif  (intégré au cours)

  Devoir Formatif  « Contrôle : savoir » ;   (remédiation)

 Devoir  Formatif  «  Evaluation   savoir faire »  (remédiation)

Devoir sommatif.

Devoir certificatif : (remédiation)

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

 

Leçon

Titre

N°3

LE SECOND DEGRE :

LES  SYSTEMES D’ EQUATIONS

CHAPITRES

i9  

Exemple 1 (utilisation de la méthode par substitution.)

:i

 

 

 

 

 

 

 

COURS

 

i9  

Exemple 1 (utilisation de la méthode par substitution.)

:i

 

 

 

 

Soit le système : 

 

 

De l’ équation (2)   tirons la valeur de « y »             y =     (3)

 

 

Reportons cette valeur dans l’équation (1)

 

 

5 x² - y²   = 55   devient        5 x²  -    ²  = 55     soit     5x² -  = 55

 

 

Multiplions tous les termes par « x² »   ( voir les Théorèmes des égalités)

 

 

 

Soit    5 x 4 - 400  =  55 x²    soit l’équation :      5 x 4 - 55 x² - 400  = 0   

 

Cette équation est une « équation bicarrée »

 

Posons  x²  =  X ; x =

 

L’équation précédente  devient            5 X²  - 55 X - 400 = 0

 

Divisons tous les termes par « 5 », nous obtenons :       X² - 11 X - 80 = 0

 

Résolution de l’équation :  a = +1 ; b = - 11 ; c = -80

”  = 121  + 320 =   441

 =     = 21

 

X’ =  = 16    X’’ =   = -5

 

Seule la valeur  X’ donne  pour « x » deux valeurs calculables :

   x1  =  +    =  + 4           x2  =  -    = - 4

 

Nous  reportons ces valeurs de « x » dans l’égalité (3) nous obtenons pour « y » les deux valeurs correspondantes :

 

                       y1  =     = + 5    ;       y 2  =   =  - 5

 

 

Commentaire : La méthode par substitution, que nous venons d’employer est générale mais ce n’est pas toujours la plus simple. En particulier, lorsque dans le système, il y a symétrie entre les inconnues, c’est à dire lorsque leur permutation ne change pas  ce système, diverses combinaisons sont possibles qui facilitent la solution.

 

 

Exemple 2 : soit à  résoudre le système 

 

Si nous observons ces équations nous constatons qu’en  multipliant les termes de(2)  par « 2 » soit  2xy = 42  (3)  et en additionnant membre  à membre  (1)   et (3) 

   On obtient    x² + y ² = 100

Nous obtenons le développement du carré du binôme   « x+y »  d’où

(x + y ) ²  = 100

 

  ( x + y ) =   ±  10

 Nous sommes  ramenés au problème : calculer deux nombres  « x » et « y »  connaissant leur somme   ( x + y ) =   ±  10  et leur produit   x y = 21

 

Nous savons que ces nombres sont solutions de l’équation X² ±  10  X + 21 = 0

 

Résolution : 

        a = +1 ; b = ±  10 ;b’ = ±  5  ; c = + 21

 

   ” ‘ = 25 - 21  =  4     ;   =  2

 

X ‘  =   ±  5  +2  

 

 X’’ =   ±  5  - 2  

Ainsi :

 

             x = + 7    ;   y   = + 3

             x =  - 7     ;  y    = - 3

 

 

Exemple 3 :

 

1°) solution par substitution :

De l’équation (1) tirons la valeur  y = -x +7

 

On remplace  dans (2)   :          x ( -x + 7) = 12    soit   - x² +7x  = 12   ; 0 = x² -7x +12

 

Nous obtenons l’équation x² - 7x + 12 = 0

Résolution :

”  =  49 - 48 = 1

 

x’   =  ( - b -   ) /2   =  (7 - 1) 2  = 6 / 2 = 3

 

x’’ =   (+7 + 1) / 2  = 8/2  =  4

 

 

si  x = 3  alors y = 4   , dans  (1)        (  3 + y = 7 )

 

si  x = 4  alors   y = 3   , dans (1)       ( 4 +y = 7)

 

Pour chaque cas on applique dans (2) :  3 fois 4 = 12 ; 4 fois 3 = 12

 

Conclusion : les deux nombres sont « 3 »  et « 4 »

 

2°)  avec   l’équation :    x² -  S x +P = 0   

Nous sommes ramenés à trouver deux nombres connaissant leur somme et leur produit

 

X² -  S x +P = 0    soit      x²  - 7 x + 12 = 0

 

Résolution : voir ci dessus :    x’ = 3   et x’’ = 4

Les deux nombres ont pour valeur 3 et 4

 

 

 

Exemple 4 :

 

 

Si nous prenons comme inconnues « x » et « (-y) » le système proposé devient :

 

 

Nous sommes ramenés à trouver deux nombres « x » et « (- y) » connaissant  leur somme 17 et leur produit  60

 

Ces deux nombres  « x » et « y » sont solutions de l’équation : X² - 17 X + 60 =0

 

Soit   12 et 5

Donc si  x = 12    ,   - y  =  5   et  y = -5 

 

 

 

 

 

 

Leçon

Titre (niveau IV)

N°

TRAVAUX d ’ AUTO - FORMATION sur le second degré : résoudre le système de deux équations.-

 

TRAVAUX  N°    d ’ AUTO - FORMATION : CONTROLE

 

 

TRAVAUX N°    d ‘ AUTO - FORMATION   EVALUATION

Résoudre les systèmes :

 

1ère série : reprendre les systèmes du cours.

 

2e série

1.   

 

 

 

2.   

 

 

 

 

3.   

 

 

 

4.