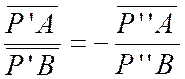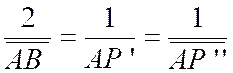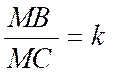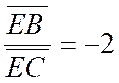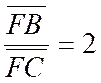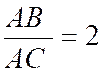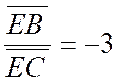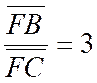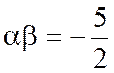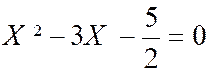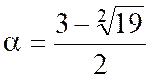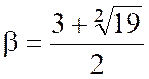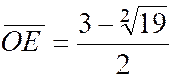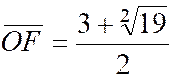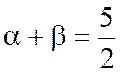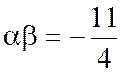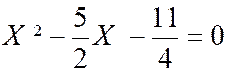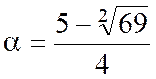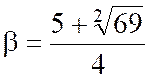« Cours » sur la division harmonique. Définition et relations .   ( Mac Laurin)  et  ( Newton ou Descartes )    

Et  des  situations problèmes

Cours

·      Soit un axe orienté , on considère deux points fixes « A » et « B »  et deux points variables «  P’ »et « P’’ »  tels que :   ( relation 1 )

                         On dit que les points  « ABP’P’’ » forment une division harmonique ou que les points « P’ P’’» divisent  « « harmoniquement » le segment « AB ».

Par ailleurs , inversement , les points « A » et « B » divisent harmoniquement le  segment « P’ P’’ »

·      Si l’on prend sur l’axe une origine arbitraire « O » et si l’on définit les points par leurs abscisses :

      ;  ;  ;

l’application de la relation de Châles permet de traduire la relation (1)  par la relation fondamentale ( 2 ) :

soit :    devient   

     ( relation 2 )

( Mac Laurin)

Si , en particulier, l’origine « O » coïncide avec le point « A », la relation ( 2 ) prend la forme réduite :

  ( relation 3 )

( Newton ou Descartes )    

                           ( relation 4 )

La forme de la relation 4 est très riche de conséquences, car elle exprime que la puissance du point « I » par rapport à un cercle de diamètre « P’P’’ » est invariable, quel que soit le couple « P’P’’ » divisant harmoniquement « AB ».

Exemple type de division harmonique :

: Soit deux sommets « C » et « B » d’un triangle et les pieds « D » et « D’ » sur ce côté des bissectrices de l’angle « A » .

On doit en particulier porter attention sur le théorème suivant : Etant donné deux points fixes « B » et « C » , et le lieu des points « M » tels que :

, « k »  étant un nombre positif donné, est le cercle ayant pour l’un de ses diamètres la distance conjugués harmoniques de « B » et « C » dans le rapport « k ».

( voir : le cercle d’Apollonius attaché au segment « BC » dans le rapport « k » )

Situation exercice 1 :

Construire un triangle connaissant la longueur du côté « BC » , la valeur de l’angle « A »  () et sachant  que : «  AB = 2 AC »

Solution :

Le segment « BC » ayant été mis en place, on construit les points « EF » tels que

  et  

« E »  est entre « B » et « C » au tiers de « CB » à partir de « C » et « F » est symétrique de « B » par rapport à « C ».

Le sommet  de () est à la fois sur le cercle de diamètre « EF », lieu des points que :

Et sur l’un ou l’autre des arcs capables de « A » décrits sur « BC » comme corde.

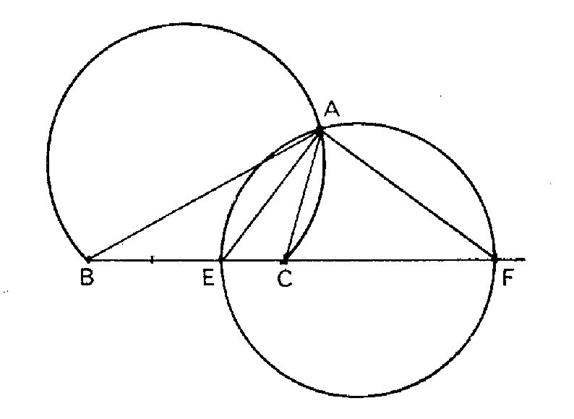
Situation exercice 2 :

Construire un triangle « ABC » connaissant la longueur du côté « BC » ,la longueur de la hauteur « AH » et sachant que « AB = 3 AC »

Solution :

1°) Mettre en place le côté « BC » et chercher les conjugués harmoniques « E » et « F » de « BC » tels que :  ;

2°) La sommet « A »  est sur le cercle de diamètre  « EF » et sur l’une ou l’autre des parallèles à « BC », s’écartant de cette droite d’une longueur égale à la hauteur donnée.

Situation exercice 3 :

                 Construire un triangle « ABC » connaissant la longueur du côté « BC » ,la longueur de la médiane  AM  issue du sommet « A » et sachant que : « AB =  k . AC » ,k étant un nombre positif donné.

Cours..

Suite !

Si l’o,n considère deux points « M’M’’ » d’un axe orienté ayant pour abscisses « x’ » et « x’’ » relativement à une origine « O », et si ces abscisses sont liées par une relation de la forme :        

A x’ x ’ ‘ + B ( x’ + x ‘ ’) + C  = 0

Il peut exister deux points fixes E F , de l’axe qui forment avec   M ’ M ’ ‘  une division harmonique.

Nous disons « il peut exister » car cette existence dépend des valeurs numériques de  « A » ; « B » , « C ».

Il sera bon de ne voir ces questions qu’après avoir acquis le maniement de l’équation du second degré. Mais c’est ici leur place naturelle.  

Problème  4

          Deux points « M ’ M ’ ‘ »  d’un axe orienté ont des abscisses , relativement, à une origine « O » liées par la relation :

2 x’ x ’ ‘ - 3   ( x’ + x ‘ ’) - 5  = 0

Démontrer qu’il existe deux points fixes « EF » tels que la division  « E F M ’ M ’ ‘ » soit harmonique.

Solution :

Désignons par  «  » et «  » les abscisses  respectives des points fixes « E » , « F » supposé exister.

D’après la formule (2)   ()  , si la division « E F M ’ M ’ ‘ » est harmonique  , on doit avoir :

Ecrivons cette relation sous la forme :

Nous nous rapprochons de la relation donnée  dans l’énoncé ::       

Ces deux relations sont identiques si l’on choisit  «  » et «  » tels que :

Ces nombres sont racines de l’équation du second degré :

               ou                

Qui a pour racines :            et  

Les points EF tels  que :

  et       divisent harmoniquement les segment « M’M’’ »

on peut se reporter au problème 4 dans la relation de Châles ;   si   est le milieu de « EF » , on peut voir que « .

Les problèmes de cette nature sont traité au niveau 4 ou niveau 3.

Problème n°5 :

Deux points  « M ’ »  « M ’’ »  d’un axe orienté ont , relativement à un origine « O » , des abscisses « x ‘ » et « x’’ »  liées par le relation :

Démontré qu’il existe deux points « E » et « F » fixes, tels que la division ( EFM’ M ’ ‘ )soit harmonique.

Solution : Prendre le problème précédent, suivre la procédure de calcul.

Rapprocher les relations :

Ramener les coefficients de « x ‘  x’’» à être égaux et égaler les autres :

D’où :

«  » et «  » sont les racines de l’équation :

    ou 

Dont les racines sont :

        et  

Problème 6 Lsans le corrigé)

Deux points  « M ’ »  « M ’’ »  d’un axe orienté ont , relativement à un origine « O » , des abscisses « x ‘ » et « x’’ »  liées par le relation :

Démontrez  qu’il existe deux points « E » et « F » fixes, tels que la division ( EFM’ M ’ ‘ )soit harmonique.

Situation exercice 1 :

Construire un triangle connaissant la longueur du côté « BC » , la valeur de l’angle « A »  () et sachant  que : «  AB = 2 AC »

Situation exercice 2 :

Construire un triangle « ABC » connaissant la longueur du côté « BC » ,la longueur de la hauteur « AH » et sachant que « AB = 3 AC »

Situation exercice 3 :

                 Construire un triangle « ABC » connaissant la longueur du côté « BC » ,la longueur de la médiane  AM  issue du sommet « A » et sachant que : « AB =  k . AC » ,k étant un nombre positif donné.

Problème  4

          Deux points « M ’ M ’ ‘ »  d’un axe orienté ont des abscisses , relativement, à une origine « O » liées par la relation :

2 x’ x ’ ‘ - 3   ( x’ + x ‘ ’) - 5  = 0

Démontrer qu’il existe deux points fixes « EF » tels que la division  « E F M ’ M ’ ‘ » soit harmonique.

Problème n°5 :

Deux points  « M ’ »  « M ’’ »  d’un axe orienté ont , relativement à un origine « O » , des abscisses « x ‘ » et « x’’ »  liées par le relation :

Démontré qu’il existe deux points « E » et « F » fixes, tels que la division ( EFM’ M ’ ‘ )soit harmonique.

Problème 6 Lsans le corrigé)

Deux points  « M ’ »  « M ’’ »  d’un axe orienté ont , relativement à un origine « O » , des abscisses « x ‘ » et « x’’ »  liées par le relation :

Démontré qu’il existe deux points « E » et « F » fixes, tels que la division ( EFM’ M ’ ‘ )soit harmonique.