FL 7 :
Pré requis
|
Fonction "généralités" |
|
|
Les Grandeurs
proportionnelles |
ENVIRONNEMENT du
dossier
|
Objectif
précédent : |
Fonction
Linéaire généralités sur la
représentation
graphique |
Sa représentation graphique.
|
TEST |
COURS |
Interdisciplinarité |
|
Représentation
graphique de l’équation y = ![]() x
x
La représentation graphique d ’
une équation passe par la recherche de
plusieurs couples de nombres ,utilisés comme
coordonnées .
Deux points suffissent pour tracer la
droite ;plus un troisième qui servira de moyen de
vérification (il doit se trouver sur cette droite )
la
représentation graphique de la fonction linéaire est une droite (noté x![]()
![]() x) ,
où l’ensemble des points A, B ,C ,D, ........ ont pour coordonnés les couples
de nombres (x ;
x) ,
où l’ensemble des points A, B ,C ,D, ........ ont pour coordonnés les couples
de nombres (x ; ![]() x )
x )
Caractéristique de cette représentation
graphique :
n
c’est une droite (D)
n
cette droite passe par l’origine « O » d ’ abscisse (0) et d’ordonnée (0) , noté (0 ;0)
n
elle possède un point caractéristique ; à d’abscisse valeur « 1 » correspond la valeur de
« ![]() » ; noté P :(1 ;
» ; noté P :(1 ; ![]() )
)
« ![]() » s’appelle coefficient directeur de la droite , c’est
un nombre relatif :, il est « positif » ,dans la représentation graphique la droite
monte de la gauche vers la droite ,on dira que la fonction est
« croissante ».,
» s’appelle coefficient directeur de la droite , c’est
un nombre relatif :, il est « positif » ,dans la représentation graphique la droite
monte de la gauche vers la droite ,on dira que la fonction est
« croissante ».,
![]() >0 ;
la droite est « croissante » ; Le coefficient directeur «
>0 ;
la droite est « croissante » ; Le coefficient directeur « ![]() » est un nombre relatif .
» est un nombre relatif .
« ![]() » peut s’appeler :
» peut s’appeler :
n
Coefficient de proportionnalité (dans le tableau)
n
Coefficient directeur de la droite de la fonction
linéaire.
n
Coefficient directeur de la droit d’équation y = ![]() x ; dans la représentation graphique
x ; dans la représentation graphique
Dans un repère cartésien orthogonal ; dans la représentation
graphique de l’équation y = ![]() x ; «
x ; «![]() » est appelé « pente de la droite », la « pente »
étant appelée aussi
« tangente » ;
» est appelé « pente de la droite », la « pente »
étant appelée aussi
« tangente » ;
la pente est obtenu par le rapport de
« y » sur
« x ».
Voir les relations trigonométriques dans un triangle rectangle
Plus
généralement :
Les
caractéristiques de la représentation graphique d’une fonction linéaire sont :
n c’est une droite (D)
n cette droite passe par l’origine « O » d ’
abscisse (0) et d’ordonnée (0) , noté
(0 ;0)
n elle possède un point caractéristique ; à d’abscisse valeur « 1 » correspond la valeur de
« a » ; noté
P :(1 ; a)
« a» s’appelle coefficient directeur de la droite , c’est
un nombre relatif :
Remarques :
si
« a » est
« positif » ,dans la représentation graphique la droite monte de la
gauche vers la droite ,on dira que la fonction est « croissante ».
si
« a » est
« négatif » ,dans la représentation graphique la droite descend du
haut gauche du repère vers le bas
droite ,on dira que la fonction est « décroissante ».
RELATION entre « a » la « représentation » de sa
valeur
« a »
est aussi appelé « PENTE » et
« TANGENTE » @
«![]() » est aussi appelé « pente »
ou « tangente » de la droite.
(voir relations trigonométriques dans le
triangle rectangle )
» est aussi appelé « pente »
ou « tangente » de la droite.
(voir relations trigonométriques dans le
triangle rectangle )
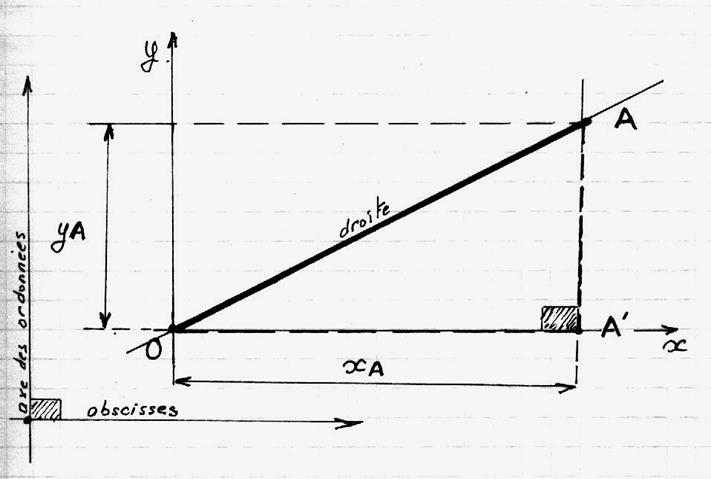
La pente est égale au rapport de la longueur
« xA » sur la
longueur « yA »
;
on dit aussi égale au rapport de la longueur du segment AA’ sur la longueur du segment OA’ ;
on dit aussi
au rapport du coté
opposé a
l’angle (AA’ ) sur le coté
adjacent (OA’)
on dit aussi égale à l’abscisse du point A sur l’ordonnée du point A
Exemples de représentations graphiques de la
fonction linéaire :
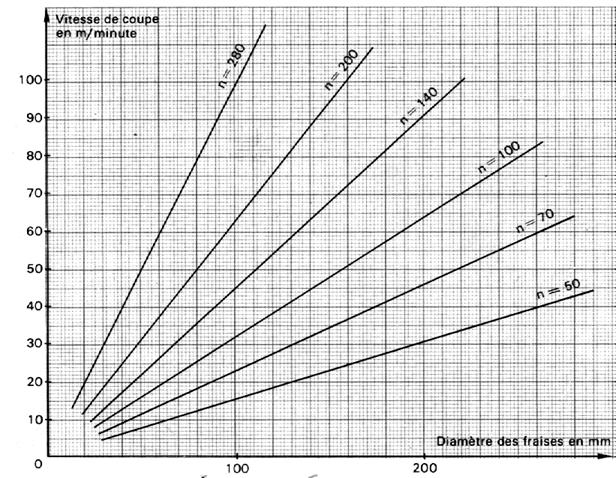
L’abaque permet de résoudre sans calcul
, par simple lecture graphique , un certain nombre de problèmes
professionnels
|
N°1 : Les abaques |
|
|
|
|
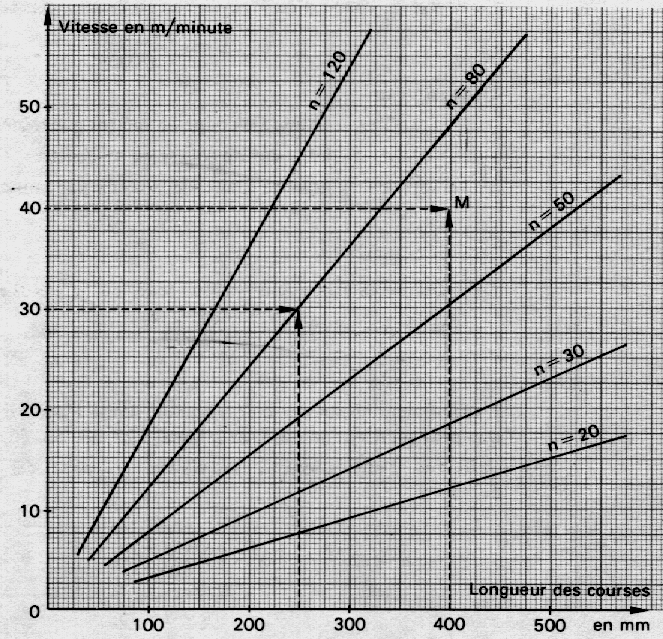
N°2 les abaques
|
|
|
|
|
Dans le dessin ci dessous , la droite passant par
« O » est une représentante de la fonction linéaire .
|
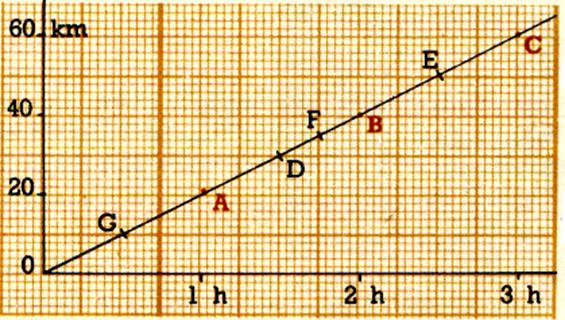
N°3 |
|
|
La distance parcourue est proportionnelle au
temps. |
|
1° ) « a » (dans le produit de facteurs associés à la
fonction linéaire) possède trois appellations , quelles sont -
elles ?
2° ) Définissez
« la représentation graphique »
précisez ,en citant les caractéristiques principales ;
placer les dans un repère cartésien.
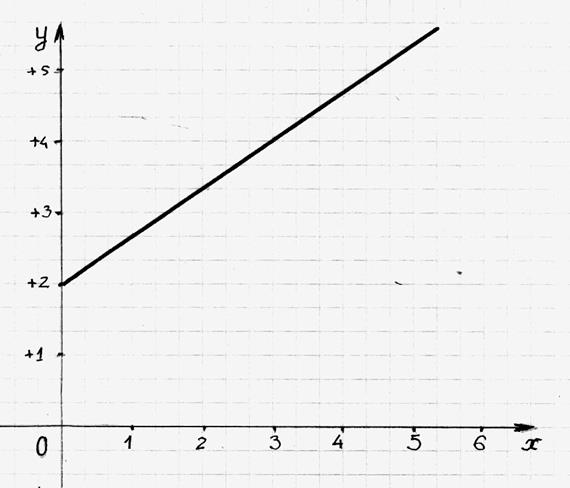
Soit les fonctions :
|
y1
= 2x |
y2
= - 2x |
y3
= - |
1°) Dans un repère cartésien orthonormé ; Faire
la représentation graphique de chaque fonction .
|
A l' équation y1 = 2x |
On associe la droite D1 (lire :droite
indice 1) |
|
A l' équation y2 = - 2x |
On associe la droite D2 (lire :droite indice 2) |
|
A l' équation y3 = - |
On associe la droite D3 (lire :droite
indice 3) |
2°) En
étudiant le graphique , donner les coordonnées du
point d’intersection des deux droites D1 et D2;
3°)
tracer D3
Ensuite : avec un rapporteur donner la valeur de l’angle faite entre les
droites D1 et D3 .
Quel commentaire pouvez-vous avoir sur la position des droites l’une par
rapport à l’autre ?
4° ) Faite le calcul du produit
a1 par a3 .
5°) tracer la droite d'équation y4 = ![]()
mesurer l’angle fait par D2 et D4 ; faire le produit a2 a4
6°)comparer les résultats
de la question 4° et 5° ; quelle
conclusion peut - on en tirer ?