FG 1	DOSSIER : FONCTIONS (généralités)  /           Objectif cours 38

Pré requis

Calcul algébrique
Les tableaux et la proportionnalité
Les tables de Pythagore

ENVIRONNEMENT du dossier

INDEX warmaths	Objectif précédent : Savoir lire et construire un tableau à double entrées :	Objectif suivant : 1°) Etude d’une fonction.	Tableau       1°)Fonctions ( présentation)

DOSSIER :  LES FONCTIONS  « généralités » …Les tableaux numériques à double entrées  et les « tableaux de variation ».

 

	I )  TABLEAU NUMERIQUE  à double entrées
	2° ) Application:
	3°) Exploitation d ' un tableau de variation:

 

 

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité    1°)Tableaux numériques

Corrigé Contrôle

Corrigé évaluation

 

 

 

 

 

 

 

COURS

 

I )  TABLEAU NUMERIQUE  à double entrées pour le tracé d’une fonction.

 

 

On peut reconnaître une fonction à partir  d ' un tableau numérique  que l’on appellera  "tableau de variation"

 

(pour "variation voir "variable" )

Variable :  on appelle « variable » une lettre  (généralement « ») à qui l’on affecte différentes valeurs numériques.  (la valeur de «  » choisie fait varier le valeur de «  » à partir d’une relation mathématique donnée.

 

« Construction » d' un tableau « de variation des valeurs de  » :

 

Ce tableau se compose de deux lignes et d' une quantité  , qui peut être illimité , de colonnes

 

 

Lieu où l'on écrit   la  Âelation entre la ligne I et II	I	Ligne  I	Ligne des ""
	II	Ligne II	Ligne des

 

La ligne I   est la ligne contenant les nombres de l 'ensemble de départ ( D)

       Cette ligne  s 'appellera "ligne des variables"  (ou ligne des ""  ) ;

                 dans les cases vous mettrez les valeurs que vous aurez choisies

 

La ligne II est la ligne contenant les nombres de l 'ensemble d ' arrivée   ( A ) 

     Cette ligne  s ' appellera "ligne des "" ou ligne des

                 dans ces cases vous mettrez les nombres que vous aurez trouvés  par calcul. 

 

          Pour obtenir la valeur de  lire :  en fonction de "  ;  on prend la valeur de " , on prendra la relation mathématique (Â ) se trouvant dans la colonne située à l ' extrême  gauche du tableau . on remplacera " par la valeur choisie , on effectuera le calcul , on reportera le résultat.

 

 

 

 

 

 

2°) Application:

 

Construire un tableau de variation à partir de  l ' expression donnée.

On donne une expression mathématique exprimée en fonction  de "x" tel que "5x+3"

 Que l 'on traduit par l ' égalité     :    

 

On peut , ainsi ,   établir un tableau de variation:

 

On  transforme le tableau « théorique » suivant:

Â	I	Ligne  I	Ligne des
	II	Ligne II	Ligne des

 

 

 

En tableau:

		3	4	6	10	100
		18	23	33	53	503

 

 

 

 

 

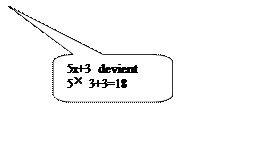
Commentaire :     j     ' ai fixé des valeurs de  = {3 ; 4 ; 5 ; 6 ; 10 ;100} (ensemble de départ)

 

J ' ai obtenu l ' ensemble d ' arrivée :   = {18 ; 23 ; 33 ; 53 ; 503 }

 

 

 

 

 

 

 

3°) Exploitation d ' un tableau de variation:

 

 

Le tableau se compose  de deux lignes et de colonnes (il y a autant de colonnes numériques que de valeurs de "x" choisies (judicieusement afin d ' avoir des calculs faciles à faire) 

 

 

  Chaque colonne contient un couple de nombres de la forme :  ( x ; f (x) )

 

Dans un tableau 

  à  x₁  on fait correspondre f (x₁)  ; à  x₂  on fait correspondre f (x₂); à  x₃  on fait correspondre f (x₃) ; et ainsi de suite  …..

 

5x +3	x	x1  =     3	x2    =  4	x3    =  6	x4  =    10	x5 =  100
	f (x)	f (x1)  = 18	f (x2)  = 23	f (x3)  =33	f (x4)= 53	f (x5) =503

 

 

 

Si l 'on nomme  chaque colonnes par une lettre majuscule ( exemple A ) si on remplace l ' écriture f (x) par "y"  , je peux identifier chaque colonne  de la façon suivante :  A ( x ; y )

  Je peux alors  utiliser les couples de points pour construire une représentation graphique dans un repère cartésien  ou

 

  A représente  le nom d 'un point dans le repère

"x" est  la valeur numérique de l ' abscisse et "y" l ' ordonnée de ce point

 

Nous pourrons  construire alors le tableau suivant:

L' expression f (x) = 5x + 3   deviendra  l ' équation  y = 5x + 3

Puisqu ' à  f (x)  correspond "y"

 

 

 

y = 5x + 3		A	B	C	D	E
à x	x	xA  =     3	xB   =  4	xC    =  6	xD  =    10	xE =  100
f (x)	y	yA  = 18	yB  = 23	yC  =33	yD= 53	yE=503

 

 

Remarques :

1 )Chaque couple de nombres indique les coordonnées des points  A ; B ;……

……

 

2 )  Dans la représentation graphique  le point A  a pour  coordonnées :

L ' abscisse  : le nombre x_A

L ' ordonnée : le nombre y_A

 

3 ) L ' ensemble des couples  (x_{A ;} y_A );  (x_B ; y_B) ; (x_C ; y_C) ; (x_D ; y_D) ; (x_E ; y_E ) représente le graphe de la fonction : y = 5x + 3

 

Commentaire:

 

  Un tableau de variation est le représentant d ' une fonction si à une valeur de (x) correspond une seule ( au plus ) valeur de "y".

Il est de la forme:

y = Relation en f (x)		A	B	C	D	E
	x	xA	xB	xC   ; xD ;   xE :    « ligne des abscisses »
	y	yA	yB	yC ; yD ;  yE   ; « ligne des ordonnées »

Où:

  Dans la représentation graphique  le point A  a pour  coordonnées :

L ' abscisse  : le nombre x_A

L ' ordonnée : le nombre y_A

 

 Et   l ' ensemble des couples  (x_{A ;} y_A );  (x_B ; y_B) ; (x_C ; y_C) ; (x_D ; y_D) ; (x_E ; y_E ) représente le graphe de la fonction : y = f(x)

 

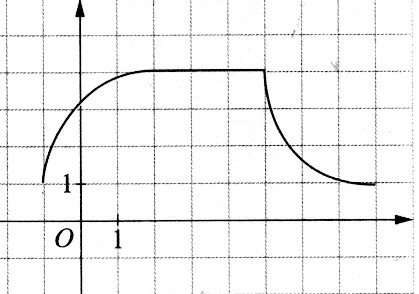
II )  Tableau de variation utilisé pour l’étude des fonctions :

 

 

Exemple type :

x	-¥                                0                                     +¥
f(x)	Il faut placer une ou plusieurs flèches pour indiquer le sens croissant ou décroissant du tracé . Cette étude de variation peut se limiter à un intervalle  noté [a ;b ] , de « x »   (@ info +++)

 

Pour le remplir on cherche des réponses à une série de  questions : (les réponses sont obtenues par calculs ou par expériences )

 

Exemple :

f(x) = -3x

 

Domaine de définition d’une fonction :  noté : D  f

Quelles sont les limites ou bornes l’application de la fonction ?

Pour quelle valeur la fonction est-elle applicable ?

      On appelle cela le domaine de définition qui nous donne l’ensemble de définition. 

Exemple  pour f(x) = -3x    : D  f =  R

Les bornes sont  « moins l’infini : -¥ »   et « plus l’infini : +¥ »

 

Que se passe –t-il aux bornes  du  domaine de définition ?

      On appelle cela l’ étude aux bornes du domaine de définition Df:

a)    que se passe-t-il pour  f (x)  quand « x » tend vers -¥ ?

f (x) tend vers +¥  quand « x » tend vers -¥ 

b) que se passe-t-il pour  f (x)  quand « x » tend vers +¥ ?

f (x) tend vers -¥  quand « x » tend vers +¥ 

c) que se passe-t-il pour  f (x)  quand « x » = 0

f (o) = o

d) résoudre  f (x) = o    0 = -3 x         donc x = 0

Que se passe –t-il entre les bornes ?

 la « ligne » est –elle croissante ou décroissante ?

on dit que l’ on cherche le sens de  variation

pour le savoir on  calcule le « taux d’accroissement » ou on « regarde » le signe du  « a »

 Exemple  pour f(x) = -3x          le coefficient de « x » est négatif  ( a = -3 ) ,

On en déduit que :  f est donc strictement décroissante dur Df

 

A partir de tous ces informations on « construit »  le tableau de variation :

Exemple  pour f(x) = -3x  , nous avons le tableau :

x	-¥                                0                                     +¥
f(x)	+¥                                         0                                                                              -¥

 

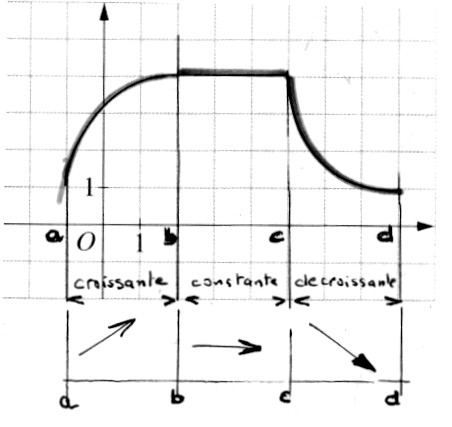
Exemple d’une étude :

- On identifie des segments différents. - On détermine des intervalles. - Dans un tableau , on indique par une flèche, si dans l’intervalle choisi la fonction est croissante , décroissante, ou constante.

 

EXEMPLE de tableaux  utilisés :

Exemple 1:

 

ensembles
D	x	3,5	7,7	8,3	10,9	13,2	17,5
A	f(x)	1	3	5	7	9	10

 

 

 

Exemple 2 :

 

ensembles
D	x	3,5	7,7	8,3	10,9	13,2	17,5
A	f(x)	1	3	5	7	9 et 3	10

 

Analyse des deux exemples :

L ' exemple 1 représente une fonction ;

l ' exemple  2 ne représente pas une fonction : l ' élément  13,2 de l ' ensemble de départ à deux éléments  9 et 3 dans l ' ensemble d' arrivée.

 

 

 

 

 

TRAVAUX AUTO - FORMATIFS et devoir.

 

 

Nom:

Prénom:

Date:

Classe:

 

CONTROLE:

 

Répondre aux questions suivantes:

 

 

1 ) Qu' appelle -  t - on « variable » ?

 

2 ) Quel rôle joue la variable  , par quelle lettre la désigne - t on ?

 

3 ) Construire un modèle de  tableau de variation.

Indiquer toutes les informations  nécessaire à son exploitation construction du graphe et de la représentation graphique.

 

4 ) Quelle condition faut - il pour qu 'un tableau    de variation soit le représentant d ' une fonction ?

 

5 ) Traduire en langage littéral : x  Î E        et             y Π F

 

 

EVALUATION:  les tableaux numériques

 

 

Dire si  la relation qui existe entre les éléments de l 'ensemble  de départ E et les éléments de l ' ensemble d ' arrivée F est une fonction ?  justifier votre réponse.

 

x  Î E        et             y Π F

 

 

 

 

 

 

 

 

	0	1		3
		3		3	5		5

 

TABLEAUX « applications »:

 

 

Soit    un "réel" quelconque .A chaque valeur de on fait correspondre son image

Compléter le tableau :

 

x	-2	-1	0	1	2	3	4
y

 

 

Soit  "x"  un "réel" quelconque .

 

A chaque valeur de "x" on fait correspondre son image     y = -3 x +2

Compléter le tableau :

 

 

Soit  "d" un réel tel que :  0 £  d   £ 5

A chaque valeur de d , on fait correspondre le réel p tel que p = 6,28 d

 

Compléter le tableau :

d	0	1	2	3	4	5
p

 

 

Soit "x"  un nombre réel quelconque.

A chaque valeur de "x" faire correspondre son double y

 

a) On appelle f cette fonction . Donner f(x)

b) Compléter le tableau:

 

x	-2	-1	0	1	2	3	5
y