DOC. : Professeur ; Formateur

DOC : Formation Individualisée

DOC : Elève.

TRANSITION / COLLEGE / LYCEE.

Information « TRAVAUX » Cliquer sur le mot !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU :Formation Niveau V

OBJECTIFS :- Savoir

I ) Pré requis:

i9	:i
i9	:i

II ) ENVIRONNEMENT du dossier :

Index

Dossier précédent :

Dossier suivant : Voir liste des cours de statistiques

Info : Cours niveau V : Leçon 1 : représentations graphiques Leçon 2 :Calculs.

III) LECON n° : RESUME en STATISTIQUES

Chapitres :

i9	Présentation d'une situation.	:i
i9	MEDIANE	:i
i9	MOYENNE	:i
i9	REPRESENTATION GRAPHIQUE	:i

IV) INFORMATIONS «  formation leçon » :

Test	RESUME	Travaux auto - formation.			Corrigé des travaux auto - formation.
		Contrôle	évaluation	INTERDISCIPLINARITE	Corrigé Contrôle	Corrigé évaluation

V ) DEVOIRS ( écrits): Voir chapitre par chapitre.

Devoir diagnostique L tests.	
Devoir Auto - formatif (intégré au cours)	
Devoir Formatif « Contrôle : savoir » ; (remédiation)	
Devoir Formatif «  Evaluation  savoir faire » (remédiation)	
Devoir sommatif.	
Devoir certificatif : (remédiation)	

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°	LES STATISTIQUES

RESUME

Avant

PRESENTATION D 'UNE SITUATION

Après

Dans une classe de seconde, on demande aux élèves combien de fois ils vont au cinéma dans un mois. L'ensemble des données constitue une série statistique:

Réponses à la question :

1; 5;1 ; 3;0 2 ;1; 0; 1; 1;0;2;0;1;2;0;1;3;0;1;1;3; 2; 4;1;

On décide de regrouper ces informations sous la forme d'un tableau :

Nombre de fois au cinéma	0	1	2	3	4	5
Effectifs (concernés)	6	10	4	3	1	1

Avant

MEDIANE.

Après

· Recherche de la position de la médiane.

Les 25 valeurs obtenues peuvent être placées (rangées) dans un ordre (croissant ou décroissant).

0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	2	2	2	2	3	3	3	4	5
12 valeurs													12 valeurs

Avant

MOYENNE (arithmétique) et moyenne arithmétique pondérée.

Après

· Calcul de la moyenne. (Arithmétique)

Pour calculer la moyenne du nombre de fois qu'un élève va au cinéma (moyenne d'entrées par élève) , on effectue le quotient de la somme des "entrées " (données par élève) par le nombre d'élèves (l'effectif total).

Soit "m" la moyenne .

Données : 1; 5;1 ; 3;0 2 ;1; 0; 1; 1;0;2;0;1;2;0;1;3;0;1;1;3; 2; 4;1;

Moyenne arithmétique :

Ici la moyenne "m" est égale à :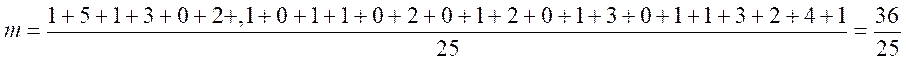

· Moyenne arithmétique pondérée:

Les données sont classées :

0

0

0

0

0

0

1

1

1

1

1

1

1

1

1

1

2

2

2

2

3

3

3

4

5

Soit ( 6´ 0 + 10 ´ 1 + 4 ´ 2 + 3 ´3 + 1´ 4 + 1´ 5 ) = 36

Les données étant classées et regroupées par valeur , le calcul devient plus simple à utiliser :

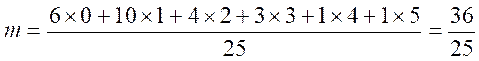
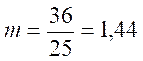
Remarque: dans le calcul d'une moyenne pondérée on "coefficiente" les valeurs .Ainsi aux valeurs ( 0; 1; 2; 3; 4; 5) on attribue les coefficient de "pondération" : 6;10;4;3;1;1.

Avant

REPRESENTATIONS GRAPHIQUES

Après

·Diagramme en bâtons:

Pour chaque valeur, on dessine un bâton dont la longueur est proportionnelle à l'effectif de cette valeur.

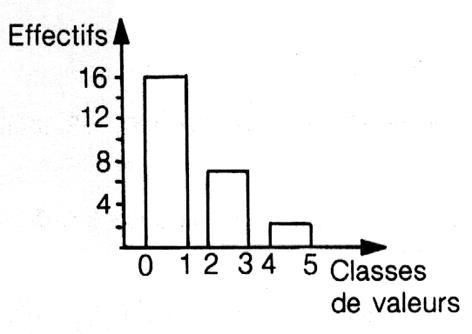
·Histogramme :

Pour l'histogramme il faut définir des "classes".

Dans l'exemple on choisit de regrouper les valeurs et faire trois classes : [0 ;1] ; [2;3]; [4;5].

On répartit les élèves en classes. -Ceux qui vont 0 ou 1 fois au cinéma. -Ceux qui vont 2 ou 3 fois au cinéma. -Ceux qui vont 4 ou 5 fois au cinéma. Ci contre la représentation graphique de l'histogramme.

Leçon	Titre
N°	TRAVAUX d ’ AUTO - FORMATION sur S

TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE

1°) Donner la définition de la médiane.

2°) A quoi est égale la moyenne arithmétique ?

3°) A quoi est égale la moyenne arithmétique pondérée?

4°)Citer deux représentations graphiques d'une série statistique .(préciser)

TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION

Voir les contrôles et évaluations des cours niveau V !!!!