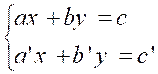Rappel :   « Solutions du système » ou « racines »

 Pré requis:

Info :  Système d’équations (définition)

Compétences :

Savoir transformer l’équation a x + by + c = 0  en une équation de la forme : y = ……

Savoir tracer une droite d’équation y = a x + b  dans un repère orthonormé.

 

ENVIRONNEMENT du dossier:

Index   « warmaths »

Objectif précédent    Rappel :   « Solutions du système » ou « racines »

Objectif suivant :

  1. Info plus sur les résolutions de systèmes.
  2. Exemples d’applications.
  3. Liste de cours sur les résolutions d’un système d’équations à deux inconnues..

Info : géné. ALGEBRE

 

Liste des cours sur les systèmes

 

DOSSIER : Les systèmes d’équations.

INFO sur Les résolutions des  SYSTEMES de deux EQUATIONS du PREMIER DEGRE A DEUX INCONNUES.

 

►       Activités en Interdisciplinarité  

 

 

RESOLUTION : il y a  3 possibilités pour résoudre ce type de système .

Info plus « cours »  ! !

 

 

1.      Résolution graphique

 Recherche des coordonnées du point d’intersection des droites  , représentantes des 2 équations du système.

Procédure :

Chaque équation du système peut avoir une représentation graphique .

Il suffit de tracer les deux droites  , les 2  équations seront  (après transformation ) de la forme «  y= ……………. » ,  partir  des équations  données dans le système  .

Pour chaque tracé :

On détermine les coordonnées de 2 points de passage de la droite

  • Pour trouver les coordonnées du  premier point : (on choisit de prendre pour   x = 0  , on calcule y = … ;. ;

 

  • Pour trouver les coordonnées du  deuxième  point : (on choisit  de prendre  y   = 0  , on calcule x = … ;. ;

 

Ensuite :  Dans  le repère on place ces deux points ; puis on trace la droite qui passe par ces  deux points.

On fait de même avec la deuxième équation ….

 

Pour trouver la solution numérique du système il sufit de relever sur le graphique les coordonnées du point d’intersection des deux droites………………………… ;;.

2.    Résolution algébrique par substitution

 

 

3.    Résolution algébrique par combinaison

 

 

 

 

 

 

Info : Exemples d’applications  

 

 

 

 

 

 

 

 

 

A savoir « EN RESUME »   !!!! :

Un système de deux équations à deux inconnues :

Peut toujours se ramener à la forme générale :                  où « a » ; « b » ; « c » ; « a ’ » ; « b’ » ;  « c’ » sont des nombres réels,  et    « x » et « y » sont les inconnues.

 

« Résoudre un système » :

Résoudre un tel système , c’est rechercher les valeurs de « x » et de « y » qui vérifient simultanément les deux équations.

« x » et « y » sont les solutions ou « racines » du système.

 

Remarque :

Suivant le système à résoudre on pourra trouver 3 types de réponse :

-         Le système possède :une solution ou racine

-          Le système possède :une infinité de solutions (ou racines)

-         Le système ne possède aucune solution ou racine

-          

 

Rappel :   « Solutions du système » ou « racines »