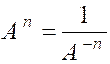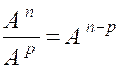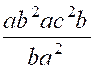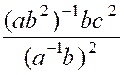Pré requis:

la multiplication de deux nombres relatifs	cliquer ici
Puissance « carrée »
Puissance « cube »
Puissance niveau 1 ( écriture normalisée )

ENVIRONNEMENT

Index : warmaths…

Objectif précédent : 1°) Puissances et écriture normalisée 2°) Multiplication de nombres relatifs cliquer ici 3°),Puissances avec des nombres relatifs.

Objectif suivant : Puissances ( carrés) d’opérations simples voir : l’exposant 0

INFO +++ : liste des cours sur les « PUISSANCES » Tableau 67

DOSSIE PUISSANCES d’un nombre dit : réel .

	1. Définition.
	2. Formules de calculs
	3. Ensemble des puissances d’un réel non nul.
TESTS	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
				Sciences PUISSANCE de dix (niveau II (6)) APPLIQUEES AUX SCIENCES

COURS :

1 - Définition.

Soit « A » un réel non nul et « n » un entier relatif.

· Pour « n 2 , « A _n » est défini comme le produit de « n » facteurs égaux à « A » .

· Pour « n = 1 » ; « A ¹ » = « A » ; par définition.

· Pour « n = 0 » , «  A ⁰=1 » ;par définition.

· Pour «  n < 0 » , « A ⁿ » est défini comme l’inverse de « A ^{– n} » ;

2 - Formules de calculs

Avec ces définitions, quels que soient les entiers relatifs « n » et « p » :

A ⁿ A ^p = A ^n+p

( A ⁿ ) ^p = A ^np

3- Ensemble des puissances d’ un réel non nul.

Le produit de puissances entières ( à exposant positif, négatif ou nul) d’un réel non nul est une puissance entière de ce nombre.

On dit que cet ensemble est stable pour la multiplication.

4 – Exercices types .

1°) « a » ; « b » et « c » sont des nombres réels non nuls. Calculer :

· «  a ³ b a ⁴ b ³  c ² a »

et

· «  b a² c a b² c³ »

2°) « a » ; « b » et « c » sont des éléments de R* ; Calculer .

· « (ab²)² b c ² a »

et

· « (abc²)³ab »

3°) « a » ; « b » et « c » sont des éléments de R* ; Calculer .

· «  a b ^-1 c b² a ^{– 2} »

et

· « b² c ^-3 b c »

4°) « a » ; « b » et « c » sont des éléments de R* ; Calculer .

· « ( ab ^-1)² bc² ab »

et

· « (a² b^-1 c)² a ^-3 b c »

5°) « a » ; « b » et « c » sont des éléments de R* ; Calculer .

·

et

·

7°) Calculer : 2³ ; 3² ; ( -2)² ; ( -2)³

8°) Calculer : ( - 3 ) ² ; ( - 2 ) ⁴ ; ( - 1) ⁵ ; ( - 1 ) ⁸

9°) Calculer : ( - 1 ) 1980 ; ( - 1 ) 1979

10°) Calculer : 2 ^-2 ; 3 ^{– 2} ; 4 ^-1 ; 6 ^-2

TRAVAUX AUTO FORMATIFS.

CONTROLE:

En rappel :

1°) Que veut dire "puissance d ' un nombre "?…

2° ) Qu'est ce qu' un nombre "pair"?

3°) Qu'est ce qu' un nombre "impair"?

Fin du rappel :

4°)« x » est un nombre relatif positif , quel est le signe de xⁿ:

5°) « x » est un nombre relatif "négatif "

- Quel sera le signe du résultat de « xⁿ » du signe ?

6 ° ) Le carré d'un nombre relatif ( positif ou négatif ) est toujours ……..

7°) Le cube d'un nombre relatif positif est …………

8°) Le cube d'un nombre relatif négatif est ……….

9°)Traduire en langage littéral de trois façon : (-3)²

10°) Pourquoi (-5)(+5) n 'est pas égal à (+5)² ou (-5)² ?

11°) Traduire en langage littéral de trois façon : (-3)³

12°) Pourquoi (-5)(+5)(-5) n 'est pas égal à (-5)³ ?

EVALUATION

1°) Faire le calcul :

4^2 =

(+4)^2 =

- 4 ^2 =

(-4)^2 =

+ 4^2 =

2°) Faire le calcul :

4^3 =

(+4)^3 =

- 4 ^3 =

(-4)^3 =

+ 4^3 =

3°) Faire le calcul :

	Réponses		Réponses
(-2)(+ 3) =		(-2)^2(-3)^3=
2(-3)(- 3) 5 =		2 ^13 ^3 (-5)^2 =

4°) Faire tous les calculs possibles :

(+4)^2 =	(-5)^2 =
(+2)^0 =	(-3,2) ^0 =
(+ 2 ) ^1=	(-3,2) ^1 =
(+2 ) =	(-3,2) =
(+2)=	(-3,2) =
(-4)^3 =	(-5)^3 =

Soit x = (+3,75)

Donner le signe du résultat de

	x^2	x^3	x^8	x^11
Signe :

Soit x = (-3,734)

Donner le signe du résultat de

	x^2	x^3	x^8	x^11
Signe :

Dire si "n" est pair ou impair ; que est le signe du résultat ?

« x ^n»	« n »	Faire le calcul :éventuellement	Analyse du résultat signe du nombre ?
(+2)^2
(+2)^3
(+2)^4
(+2)^5

Dire si "n" est pair ou impair ; que est le signe du résultat ?

« x ^n»	« n »	Calcul :	Conclusion résultat
(-2)^2
(-2)^3
(-2)4
(-2)^5
(-2)^6
(-2)^7

Algèbre : Ecrire plus simplementLsous forme de puissances .

bb par ………..			xx = ……………
aa…=	aaaaa……=..	abb……=	bbb:…=
xxx:…=	yyyy:…=… …….	xxyyy:……= ………	axxyy :…=