INFORMATIONS : on
verra les différentes règles de trois
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pré requis:
|
Fraction
équivalente |
|
|
Objectif
précédent : 1°) la règle de trois simple et directe 2°) la règle de trois simple et inverse |
1°)Pourcentage ;
tant pour cent ; tant pour mille |
DOSSIER : "la REGLE de TROIS COMPOSEE "
|
COURS |
Interdisciplinarité |
|
Notion de la règle
de Trois :
Il existe de
nombreuses relations qui se calculent uniquement au moyen de la multiplication
et de divisions successives ; ainsi ; par exemple ; j’ai acheté
15 bouteilles pour 120 € , je veux savoir combien me coûteront 40
bouteilles ; ou bien j’ai gagné 240 € en travaillant 6 jours et je veux
savoir combien on me payera en un mois de 25 jours de travail ;ou encore 5
000 € m’ont rapporté 300 € en un an et je veux savoir combien me
rapporterait dans le triple de temps une
somme de 30 000 € .
Dans tous les cas le
raisonnement est le même ; je cherche le résultat pour une unité , puis je le multiplie par le nombre d’unités .
Dans tous les exemples précédents ,
les grandeurs sont dit « directement proportionnelles » mais il y a
des cas où la relation est
inverse ; ainsi : plus j’emploie
d’ouvriers à un travail , moins
de temps il faudra pour le finir . Plus un mur est haut ,
ou épais , moins de longueur on ne pourra en faire dans un temps déterminé ou
avec une quantité de matériaux donnée , on dit dans ce cas , que la règle de trois est inverse , car les
quantités sont inversement proportionnelles .
La règle de trois est simple lorsque
le problème se réduit à une
seule relation ; et elle est composée
lorsque le problème comprend une série plus ou moins longue de rapports .
Elle est directe ou inverse selon que les
quantités sont directement ou inversement proportionnelles à la quantité
demandée.
La règle de trois
composée peut avoir à résoudre les
combinaisons les plus diverses de quantités directement et inversement proportionnelles
.
La Règle de
Trois composée
Notion : la règle de trois est composée lorsqu’elle doit résoudre toute
une série de grandeurs proportionnelles , la quantité
que l’on cherche dépendant de plus de trois quantités connues .
Dans la règle de trois composée , les grandeurs directement et inversement proportionnelles se combinent
de divers manières suivant les données du problème et il est nécessaire de
faire bien attention pour se rendre compte si la relation qui existe entre
l’inconnue et les diverses quantités données est directe ou inverse .
Ainsi le nombre de jours nécessaires pour faire un travail est
directement proportionnel à la quantité
du travail et inversement proportionnel au nombre d’ouvriers que l’on emploie
et au nombre d’heures de travail par jour . La
longueur d’un treillis métallique est directement proportionnel à la quantité
de fil de fer dont on dispose pour le faire et inversement proportionnelle à la
largeur que l’on donne au treillis .
Le temps nécessaire pour qu’une somme
produise un intérêt déterminé est inversement proportionnel au capital engagé
et au taux .
Problème
type :
Quinze ouvriers , en 12 jours de 10 heures font 180 m de clôture. Combien
faudra-t-il de jours de 8 heures à 25 ouvriers pour faire 450 m .
|
Grandeurs |
N
d’ouv. |
N.
de jours |
N.
d’heures |
N de
mètres |
|
1re
valeur |
15
ouv. |
12
j. |
10
h. |
180
m |
|
2e
valeur |
25
ouv. |
X j |
8 h |
450
m |
Méthode de réduction à l’unité .
1° Si les 15 ouvriers mettent 12 jours pour faire un travail , un
ouvrier mettra 15 fois plus de jours ,
ou 12 fois 15 , et 25 ouvriers mettront 25 fois moins de jours qu’un seul ,
ou :
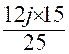
2° Quand la journée est de 10 heures , il faut ![]() jours ; si la
journée était de une heure , il en
faudrait 10 fois plus , ou :
jours ; si la
journée était de une heure , il en
faudrait 10 fois plus , ou : ![]() et quand elle est de
8 heures , il en faut 8 fois moins ou :
et quand elle est de
8 heures , il en faut 8 fois moins ou :
![]()
3°)Pour faire 180 mètres , il
faut ![]() jours ;pour faire
un mètre , il faudrait 180 fois moins de jours , ou
jours ;pour faire
un mètre , il faudrait 180 fois moins de jours , ou ![]() et pour faire 450
mètres , il en faut 450 fois plus ou :
et pour faire 450
mètres , il en faut 450 fois plus ou : ![]() = 22 jours ½
= 22 jours ½
Avant d’effectuer les calculs , on a soin de
simplifier l’expression.
Remarque :
certains problèmes qui semblent devoir se résoudre par une règle de trois composée , peuvent se
ramener à une solution plus simple .
Exemple :
15 ouvriers en 12 jours de 10 h ont fait un certain ouvrage . Combien faudrait-il de journées de 8 h à 25 ouvriers
pour faire le même ouvrage ?
Nombre de jours = 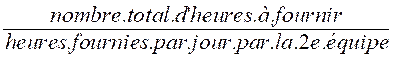
Nombre d’heures à fournir : ( 10![]() 15
15![]() 12) heures.
12) heures.
La 2e équipe fournit par jour ( 8![]() 25) heures
25) heures
La 2e équipe mettra ![]() = 9 jours
= 9 jours
TRAVAUX AUTO FORMATIFS.
Compléter la phrase suivante :
la règle de trois est composée lorsqu’elle doit
résoudre toute une série de grandeurs proportionnelles ,
la quantité que l’on cherche dépendant de plus de
trois quantités connues .
1°) Pour 20 lampes électriques fonctionnant 4 h par
jour , on
dépense 5 € par jour . Quelle
serait la dépense pour 17 lampes fonctionnant 6 h par jour.
2°)Un salarié qui a travaillé 8j et 9h par jour , a
reçu 400 € . Que recevrait-il pour 17
journées de 8 heures ?
3°) Douze ouvriers ont mis 15 jours pour faire 120
m d’ouvrage. Combien 30 ouvriers
feront-ils de mètres du même ouvrage en 10 jours ?