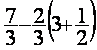CORRIGE

Vers le sujet :N°2 seconde lycée

Ex.1

1) Calculer et présenter le résultat sous forme d’une fraction irréductible :

A =

Corrigé :

1°) on constate que A = est de la forme  ;avec N = et D =

commentaire :

2°) Il faut calculer pour que N et D deviennent une fraction ; de sorte de calculer la division d’une fraction par une autre fraction.

3°)Calcul de N : = ; ( soustraction entre deux fraction de dénominateur différent)

a)On recherche le dénominateur commun entre  ;

le dénominateur commun est 4 fois 6 = 24 ;

b) on transforme la fraction  :  ; x =24 fois 3 divisé par 4 ; soit 6 fois 3 = 18 ;

c) on transforme la fraction  : ; x = 24 fois 5 divisé par 6 ; soit 4 fois 5 ;

d ) le calcul (impossible) de devient le calcul possible

= ;

il faut calculer 18 – 20 = (+18) + ( - 20) = - 2 ( SOS cours ! ! ! !)

donc = soit

4°) Calcul de D  = ( soustraction entre une fraction et d’un nombre )

a) devient

b) le dénominateur commun est « 4 » ainsi : devient

calcul de =  ;

=

ainsi : = ou sous forme décimale : = - 0,75

5°) on donne A =  ; A est de la forme  ;

avec N =devient et D = devient

A = = = ( voir la division d’une fraction par une autre fraction. )

= = = = = =

Conclusion : A = =

B =

B =  ; voir INFO sur l’ exemple de la forme a – b ( c + d )

on remarque que B est de la forme a – b ( c + d ) (voir exemple ci dessus )

a) on calcule (c + d)  : 3 +

3 + = = = = (forme décimale = 3,5)

on remplace le résultat  ainsi B devient = à

b) on calcule b ( résultat de c + d )

calcul de

remarques :

- pour le calcul on ne s’occupe pas du signe « -  » 

- transformation de l’écriture : qui devient =

= après simplification on obtient  ;

le résultat de  « b ( résultat de c + d ) » =

ainsi – b ( c + d ) = -

On termine le calcul de B = a – b ( c + d )

Il y a deux façons de procéder :

« a plus le résultat de (– b ( c + d )) » = a +(– b ( c + d )) 

On aurait tout aussi bien dire «  a moins le résultat de b ( c + d ) » = a - b ( c + d ) 

Ce qui se traduit par : a + (– b ( c + d )) = a – b ( c + d )

« a » = ; et – b ( c + d ) = -  ;

a - b ( c + d )  = -

=

=

B =

B = 0

2) Ecrire sous la forme aⁿ avec n Î Z : SOS Cours : cliquez ici

C = ; D = ; E = ( 2³ )² 2

3) Ecrire sous la forme a : F = + 3 -

4) Ecrire sans radicaux au dénominateur : G = ; H =

Ex.2 : Calculer : A = ( 2- )²

B = ( 3 + 2 ) ²

C = ( 2+1 ) ( 2- 1 )

Ex.3 :

1) les nombres 239 et 637 sont-ils des nombres premiers ? Justifier vos réponses.

2) Les nombres 56 et 105 sont-ils premiers entre eux ? Justifier votre réponse .

3) Ecrire sous forme d’une fraction irréductible le nombre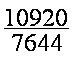

( barème : 11 – 3 - 6 )