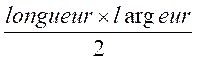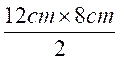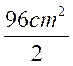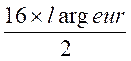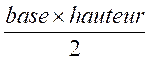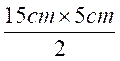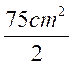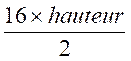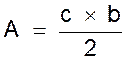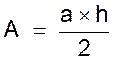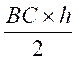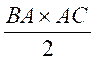|
|
|
|
|
|
|
Les Aires |
|
|
Aire d’un triangle |
|
|
|
|
ENVIRONNEMENT du
dossier:
|
Objectif précédent : |
Retour vers la
liste des objectifs de formation |
tableau |
|||
|
|
|||||
|
|
DOSSIER : Calculs
de l’ AIRE du TRIANGLE RECTANGLE |
|
|||
|
|
A
savoir : définition . |
|
|||
|
|
Les applications directes . |
|
|||
|
|
Les applications indirectes . |
|
|||
|
|
CAS d’ égalité des deux
formules : |
|
|||
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
A
savoir : définition |
|
|
|
|
|
|
|
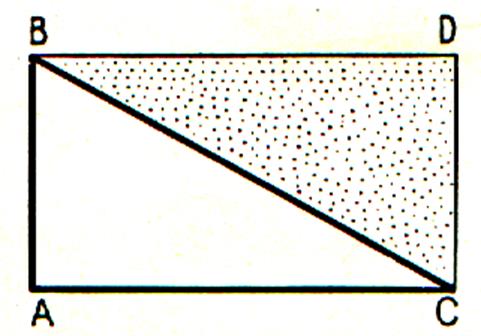
L ‘
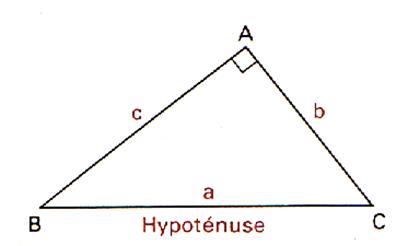
aire d’un triangle rectangle : Par définition : L’aire d’un triangle rectangle est égale
à l’aire du rectangle dont on connaît la longueur de la longueur et la
longueur de la largeur. Remarque :
les longueurs doivent être exprimées dans la même unité de longueur |
|
|
|
|
|
|
|
|
|
|
|
L application directe . |
|
|
|
|
|
|
|
1ième cas : CALCUL de l’aire
avec les mesures des cotés formant l’angle droit : |
|
|
|
|
|
|
|
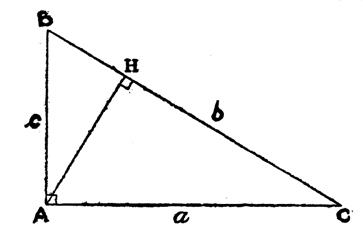
On connaît
les longueurs des cotés « c » et
« b » formant l’angle droit , dans ce cas
nous calculons le produit des deux longueurs divisé par deux. A =
|
|
|
|
Application 1 : Soit un triangle rectangle ; les deux
cotés de l’angle droit mesure respectivement
12 cm et 8 cm. Calculer son
aire: A = A = A = 48 cm2 |
|
|
|
Les applications indirectes . |
|
|
|
|
|
|
|
Niveau ++++ |
|
|
|
Application 2: La surface du triangle est égale à 40 cm2
, un de ces cotés de l’angle droit vaut 16 cm .Quelle est la longueur de
l’autre côté?
Résolution : 40 =
on remplace la longueur par sa valeur : 40 = on multiplie les deux membres par « 2 » 2 on effectue les calculs
80 = 16
la
largeur = 5 cm |
|
|
|
Application 3: La surface du triangle est égale à 40 cm2
, un de ces cotés de l’angle droit vaut 5 cm .Quelle est la longueur de l’autre
côté?
Résolution : voir exemple précédent
On trouve : la longueur de la longueur est égale
à 16 cm |
|
|
|
|
|
|
|
2er
cas :CALCULS de l’aire avec la base et
la hauteur : |
|
|
|
|
|
|
|
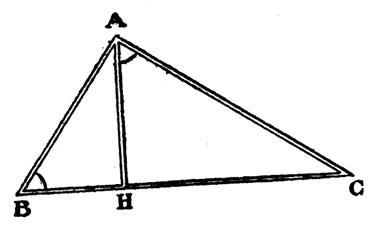
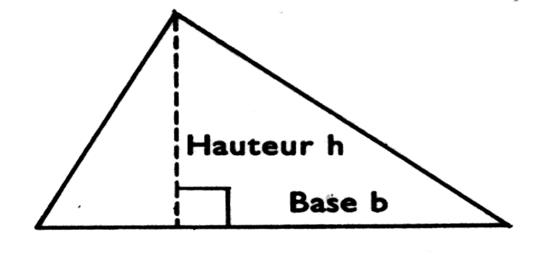
On
connaît la longueur de l’hypoténuse (appelée : base )
et la longueur de la hauteur (issue de la base): Aire
= (base fois hauteur) divisé par deux A =
|
|
|
|
Application N°1
Un triangle rectangle à pour base 15 cm et pour hauteur 5 cm. Calculer son
aire. Résolution :
On sait que A = A = A = A = 37,5 cm2 |
|
|
|
Niveau +++++ |
|
|
|
A ) La
surface du triangle est égale à 40 cm2 , sa base vaut 16 cm
.Quelle est la longueur de sa hauteur?
|
|
|
|
Résolution : 40 =
40 = 2 80= 16
h = 5 cm |
|
|
|
|
|
|
|
B ) La
surface du triangle est égale à 40 cm2 , sa hauteur vaut 5 cm
.Quelle est la longueur de sa base ?
|
|
|
|
Résolution : Voir ci dessus : la base à pour
longueur 16 cm |
|
|
|
|
|
|
|
CAS d’ égalité des deux
formules : |
|
|
|
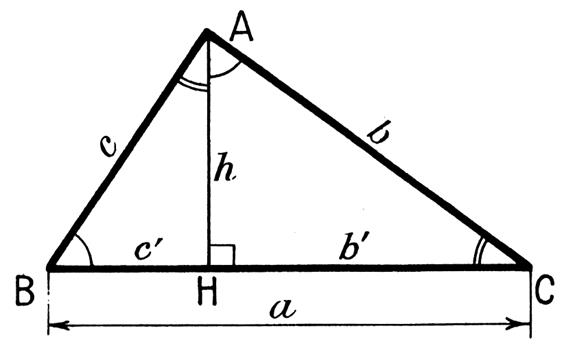
Rappel : (voir les relations
métriques dans le triangle rectangle) |
|
|
|
Première formule : A1 = Soit
= Deuxième formule : A2 = Soit = |
|
|
|
|
|
|
|
|
|
|
|
Pour
un même triangle rectangle les formules sont équivalentes : A1 = A2 On peut écrire : Ce
qui donne : ce
qui donne après simplification : BC |
|
|
|
|
|
|
|
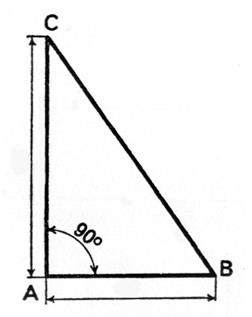
Application : Dans un triangle rectangle on
nous donne
BC = ? h = ? BA = 16 cm AC = 5 cm On
veut connaître la longueur de l’hypoténuse et la longueur de la hauteur. Résolution : il faut calculer BC pour trouver la valeur
de « h » ( voir Pythagore) |
|
|
|
Résolution : On
sait que dans un triangle
rectangle BC |
|
|
|
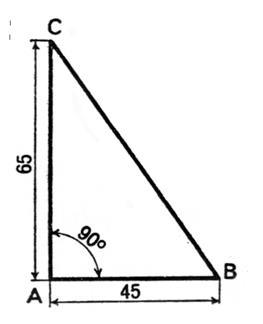
Aire
du triangle rectangle : (65 fois 45) divisé par 2
|
|
|
|
Calculer
l’aire du triangle tel que CA =
………… ; AB = ………………
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
||||
|
|
CONTROLE : 1 ) A
quoi est égale l’ aire du triangle rectangle
? 2 )
Donner les deux formules permettant de calculer l’aire d’un triangle
rectangle (compléter avec un dessin coté ) EVALUATION Donner les formules ; remplacer les lettres
par les valeurs données , faire les calculs Compléter
le tableau suivant : |
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
1 |
2 |
3 |
4 |
|||
|
Grand coté « G » |
18 m |
|
40 |
|
||
|
Petit coté « l » |
5 m |
|
|
35 |
||
|
Hypoténuse « L » |
Voir « Pythagore »
|
45 cm |
50 |
65 |
||
|
Hauteur « H » |
12 cm |
|
|
|||
|
Aire « A » |
20 m2 |
270
cm2 |
|
|
||
|
Périmètre « P » |
|
|
|
|||
Les exercices « 3 » et
« 4 » ne sont complètement réalisables que si l’on connaît les : relations métriques dans le triangle rectangle