Pré requis:
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
AVANT :
|
APRES :
1°) Le triangle équilatéral et
ses caractéristiques. |
1.
Complément
d’Info : la géométrie plane
|
||
|
|
|
|
|
|
TITRE : LE TRIANGLE
REGULIER (dit aussi EQUILATERAL )
|
|
|
|
|
||||
|
|
I
) CONSTRUCTION D’UN HEXAGONE REGULIER. |
|
|
||||
|
|
II
) Diviser
un cercle en six parties égales. |
|
|
||||
|
|
III
) CONSTRUIRE UN TRIANGLE EQUILATERAL ( Régulier) |
|
|
||||
|
|
IV ) Recherche des propriétés du segment AH . |
|
|
||||
|
|
V
) Les
hauteurs |
|
|
||||
|
|
|
||||||
Travaux ; devoirs
|
|
Corrigé
|
|
||||
|
|
Contrôle |
évaluation |
|||||
|
Interdisciplinarités : (matière concernée) |
|||||||||
|
F |
H |
Géo. |
Autres : |
Sciences et technique |
Physique Chimie Electricité |
Statistique. |
|
|
|
COURS
|
I
)
CONSTRUCTION D’UN HEXAGONE REGULIER. |
|
||
|
|
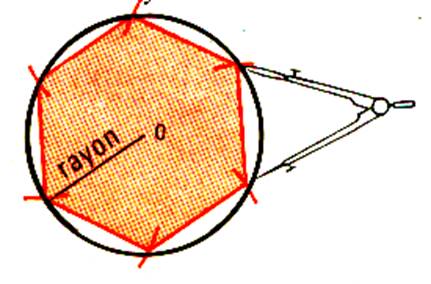
Tracer un cercle de 5cm de rayon
. Partageons ce cercle en parties égales en portant 6 fois le raton. Joignons les
points pour obtenir une figure. La figure colorié est appelée un hexagone régulier . |
|
|
|
|
TRAVAUX PRATIQUES : |
|
|
|
|
II
) Diviser
un cercle en 6 parties égales |
|
|
|
|
|
|
|
|
|
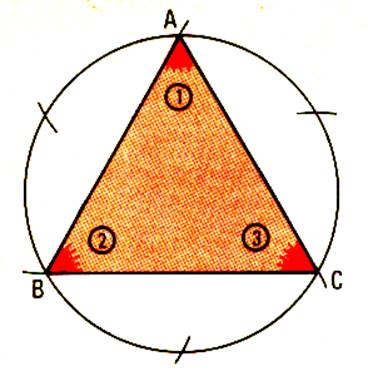
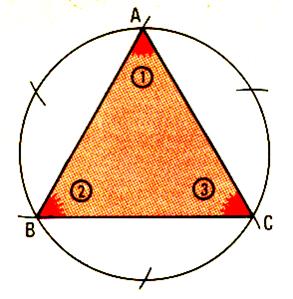
Activité 1 : Après avoir diviser un cercle en 6 parties égales , joindre les points obtenus de deux en deux
.Constat : La figure est limitée par 3 segments : Elle possède : ·
3 côtés. · 3 angles · 3 sommets Cette figure est appelée : un triangle . |
|
|
|
|
Mesurerons par comparaison les longueurs et les
angles |
|
|
|
|
Pour les longueurs prenons une bandelette : On constate que les trois
côtés sont de même longueur. |
|
|
|
|
Avec une feuille de calque. Calquons l’angle 1 et vérifions par superposition que les
angles 2 et 3 sont égaux à l’angle 1 |
|
|
|
Nous pourrions mesurer les longueurs des segments
et des angles. |
|
||
|
|
III ) Activité
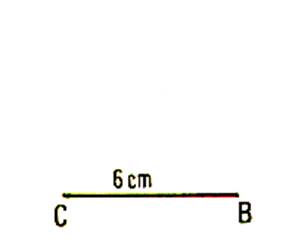
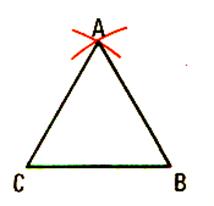
2 : CONSTRUIRE UN TRIANGLE EQUILATERAL ( Régulier) Sur une feuille de papier tracer un triangle dont un côté mesure 6cm .avec le compas et
la règle graduée. |
|
|
|
|
Tracer un segment de Régler l’écartement du compas = |
|
|
|
|
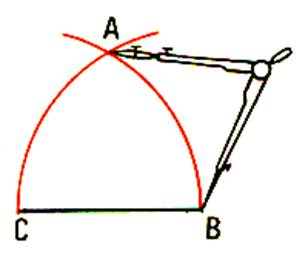
De C et B comme centre ; tracer deux arcs de
cercle , se coupant en A |
|
|
|
|
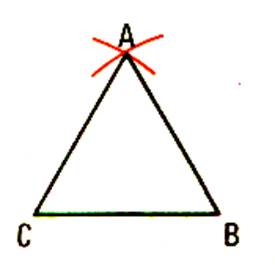
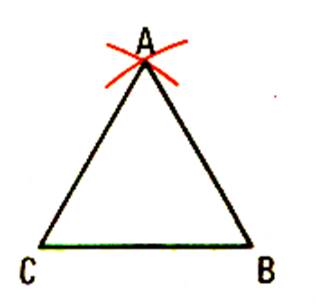
Tracer les segment CA et BA |
|
|
|
|
Activité 3 : |
|
|
|
|
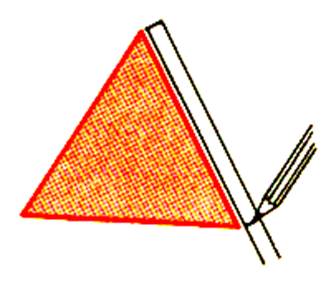
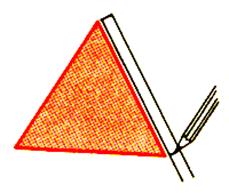
Découper le triangle précédent |
|
|
|
|
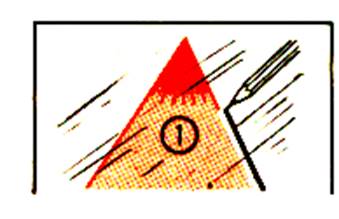
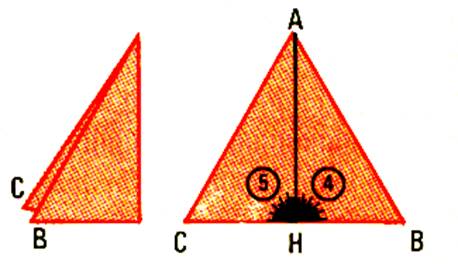
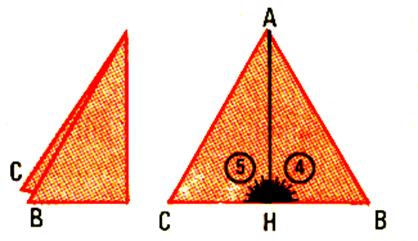
Plions en deux le triangle
« équilatéral » obtenu. Déplier et marquer d’ un trait noir le pli . Nous avons un trait AH |
|
|
|
|
IV ) Recherche des propriétés du segment AH . a)
A l’aide de l’équerre
ou du rapporteur vérifier que les angles 4
et 5 sont des angles droits . b)
Le segment AH est perpendiculaire au segment CB . On dira que
le segment AH est la hauteur
du triangle et que le côté CB sur
repose la hauteur est la base du
triangle . Activité 4 : |
|
|
|
|
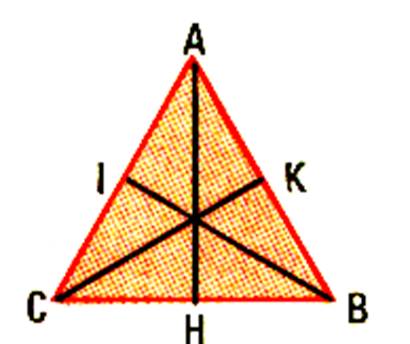
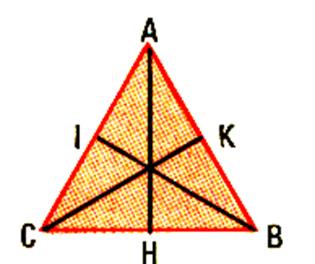
Plier deux fois encore le triangle de façon que
AC soit la base , puis que AB soit la base. Combien de hauteur a – t- il un triangle ? Le segment BI est la hauteur quand la base est AC. Le segment CK est la hauteur quand la base est
AB. |
|
|
|
|
V )
Activités complémentaires : a)
Observons le point où se croisent les hauteurs
. Que remarquons - nous ? Les hauteurs se croisent en un même point . b)
Où se trouve le point
H sur la base BC ? le point H se
trouve à égale distance de C et B . c)
Comment le segment
partage – t- il l’angle |
|
|
|
|
|
|
|
Travaux auto formatifs.
TRAVAUX PRATIQUES :
Activité
1 :
|
Après avoir diviser un cercle en 6 parties égales ,
joindre les points obtenus de deux en deux .Constat : La
figure est limitée par 3 segments : Elle possède : -……………………………….. -………………………………… -…………………………………. Cette figure est appelée : ………….. . |
|
Mesurerons par comparaison les longueurs et les angles
|
Pour les longueurs prenons une
bandelette : On constate que les trois côtés ………………………... |
|
|
Avec une feuille de calque. Calquons l’angle 1 et vérifions
par superposition que les angles 2 et
3 ……………………………………. |
|
Nous
pourrions mesurer les longueurs des segments et des angles.
Activité 2 : CONSTRUIRE UN TRIANGLE EQUILATERAL (
Régulier)
Sur une feuille de papier tracer un triangle dont un côté mesure 6cm .avec le compas et
la règle graduée.
Activité 3 :
|
Découper le triangle précédent |
|
|
Plions en deux le triangle « équilatéral » obtenu. Déplier et marquer d’ un trait noir le pli . Nous avons un trait AH |
|
Recherche
des propriétés du segment AH .
c)
A l’aide de l’équerre ou du rapporteur vérifier que les angles 4 et 5 sont des angles droits
.
d)
Le segment AH est perpendiculaire
au segment CB .
On dira que le segment AH est
……………….. du triangle
et que le côté CB sur repose la hauteur est ……………….. du triangle .
Activité 4 :
|
Plier
deux fois encore le triangle de façon que AC soit la base ,
puis que AB soit la base. Combien de hauteur a – t- il un triangle ? ………………… Le segment BI est ………………………………………………….. Le segment CK est ……………………………………………………… |
|
Activités complémentaires :
a)Observons
le point où se croisent les hauteurs . Que remarquons - nous ?
……………………………………………..
.
b) Où se trouve le point H sur la base
BC ? …………………………………………………………..
c) Comment le segment partage – t- il l’angle ![]() ? …………………………………………………………..On peut dire que AH est aussi
…………………………. de l’angle A .
? …………………………………………………………..On peut dire que AH est aussi
…………………………. de l’angle A .