|
|
|
DOSSIER : LES
QUADRILATERES ; « Définition
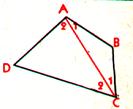
et présentation des figures »(A,B,C,D)
1. Donnez
la définition d'un quadrilatère
2. Donner
le nom de 5 quadrilatères « particuliers »
Série 1 :
1) Tracer un quadrilatère convexe.
2 ) Tracer un quadrilatère non convexe.
3°) Construire à la règle et au compas la médiatrice
( D) d'un segment AB de 6 cm de longueur . Soit
"F" le point
d'intersection de ( D)
et de [ A B ] .
Placer sur la médiatrice deux
points C et D situés de part et d'autre
de F tels que F soit le milieu de [ C
D ] . Que représente la droite ( AB) pour le segment [ CD] . Quelle est la nature du quadrilatère
ACBD ?
Série 2 :
EXERCICES DE
CONSTRUCTION :
Les parallélogrammes
|
1°)
Parallélogramme ABCD de côtés AB = 35
mm et AD = 45 mm et |
|
|
2°) Parallélogramme ABCD tel
que AB = 26 mm et AD = 48 mm et la diagonale BD = 40 mm |
|
|
3°) Parallélogramme ABCD de
côté AB = 5cm et de diagonales AC = 4 cm et BD = 80 mm |
|
|
4°) Parallélogramme ABCD tel
que AB = 2,5cm et AD = 5cm et la diagonale AC = 64 mm |
|
|
5°) Parallélogramme ABCD de côtés AB = 5cm et AD = 4cm et de
hauteur AH = 3cm |
|
|
6°) Parallélogramme ABCD de côté AB= 30 mm et de hauteurs AH = 25 mm et AK = 32 mm ( niveau +++) |
|
|
1°) Rectangle
ABCD tel que AB = 55mm et AD = 35 mm |
|
|
2°) Rectangle
ABCD de diagonale 5 cm et de côté AB = 20 mm |
|
|
3°) En +++ : Rectangle ABCD de diagonale 55 mm et tel que |
|
|
4°) En
plus : rectangle ABCD de longueur triple de la largeur et de périmètre
16 cm . |
|
|
1°)Losange ABCD tel que AB = 27 mm et |
|
|
2°) Losange ABCD
de diagonales AC = 46 mm et BD = 38 mm |
|
|
3°) Losange ABCD de diagonale BD = 4 cm et tel que |
|
|
4°) En plus : losange d’aire A = 6cm2 et de diagonale AC = 3 cm |
|
|
1°) Carré de
côté AB = 43 mm |
|
|
2°) Carré de
diagonale AC = 52 mm |
|
|
4°) En
plus : carré de périmètre p = 10
cm |
|
|
5°)En plus : carré d’aire A = 1225 mm2 |
|
|
Exercices d’identification : Soit le parallélogramme ABCD et « O »
le point d’intersection des diagonales |
|
Consignes : mettre une croix
pour les figures concernées ; justifier.
|
Propriétés ou
caractères |
trapèze |
Trapèze isocèle |
Trapèze rectangle |
parallélogramme |
rectangle |
Losange |
Carré |
justification |
AB // DC
|
|
|
|
|
|
|
|
|
|
AO =OC= OD = OB |
|
|
|
|
|
|
|
|
|
AB = BC=CD=DA |
|
|
|
|
|
|
|
|
|
AB//DC et |
|
|
|
|
|
|
|
|
|
BC // AD et |
|
|
|
|
|
|
|
|
|
AB = CD et AD = BC |
|
|
|
|
|
|
|
|
|
Rectangle et AB
= BC |
|
|
|
|
|
|
|
|
|
Parallélogramme
tel que AC ^ BD |
|
|
|
|
|
|
|
|
|
Propriétés ou
caractères
|
trapèze |
Trapèze
isocèle |
Trapèze
rectangle |
parallélogramme |
rectangle |
Losange
|
Carré
|
justification |
|
AD // BC et |
|
|
|
|
|
|
|
|
|
AB //CD Et AD // BC |
|
|
|
|
|
|
|
|
|
Losange tel que |
|
|
|
|
|
|
|
|
|
AB //DC et AB =DC=BC |
|
|
|
|
|
|
|
|
|
Médiatrice de AB et médiatrice de DC confondues |
|
|
|
|
|
|
|
|
|
AB // CD et AB = CD |
|
|
|
|
|
|
|
|
|
[AC] et [BD ] médiatrices l’une de l’autre |
|
|
|
|
|
|
|
|
|
AD // BC et AB =
CD |
|
|
|
|
|
|
|
|
|
m(A,C) = m ( B,D)= 0 |
|
|
|
|
|
|
|
|
|
Propriétés ou
caractères
|
trapèze |
Trapèze isocèle |
Trapèze rectangle |
parallélogramme |
rectangle |
Losange |
Carré |
justification |
|
Losange tel que AC = BD |
|
|
|
|
|
|
|
|
|
m(A,C) et m (B,D) = 0 et AC = BD |
|
|
|
|
|
|
|
|