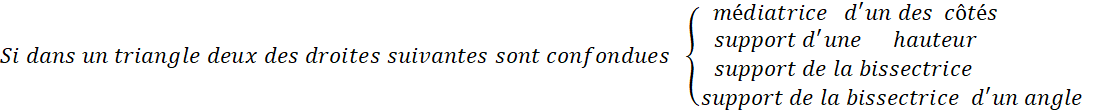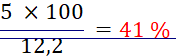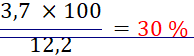ENVIRONNEMENT
du dossier:
|
|
Fiches :
sur les droites remarquables du triangle.
|
|
|
|
Fiche 1 :
Les MEDIATRICES.
|
|
|
|
Fiche 2 : Les Hauteurs.
|
|
|
|
Fiche 3 : Les Médianes.
|
|
|
|
Fiche 4 : Les
Bissectrices.
|
|
|
|
Fiche 5 : Reconnaître un
triangle isocèle.
|
|
|
|
Fiche 6 : Le triangle
équilatéral.
|
|
|
|
Fiche 7 : Activités –
Exercices.
|
|
|
|
Fiche 8 : Propriété des
points intérieurs à un triangle
équilatéral.
|
|
|
|
|
|
|
|
FICHE 9 : Application aux
statistiques. (exploitation de données
statistiques).
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|||
|
|
Fiche
1 MEDIATRICES
|
Info « médiatrice » et « médiatrice
-médiane- hauteur en collège P6 »
|
|
|
|
|
|
|
||
|
|
Vous
avez vu en 5°
et au « leçon …fiche 6… » ) que les médiatrices des côtés d'un triangle sont concourantes en
un point qui est le centre du cercle circonscrit au triangle. ·
Tracez les médiatrices du triangle
« ABC » et le cercle circonscrit à ce triangle, |
|
|
|
|
|
|
|
||
|
|
Fiche 2 : Hauteurs.
|
Info
++ @
|
|
|
|
|
On appelle « hauteur » d'un
triangle le segment limité par un sommet et son projeté
orthogonal sur le support du côté
opposé. Par
abus de langage " hauteur " désigne aussi la
droite support de ce segment. |
|
||
|
|
Activité : Tracez les hauteurs des deux
triangles ci-dessous (utilise ton équerre). |
|
||
|
|
|
|
|
|
|
|
Si votre
tracé
est bien fait, vous constatez que dans
chacun des cas, les trois hauteurs sont______________________________ …………………………… C'est ce que nous allons démontrer. |
|
||
|
|
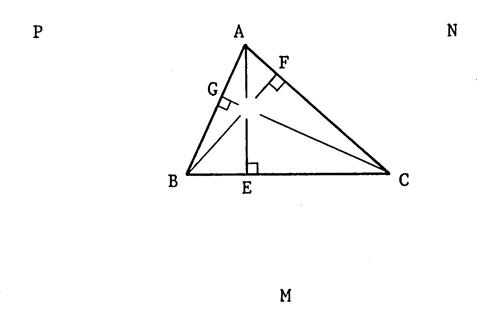
Ci-contre :
Voici un triangle ABC quelconque. [AE] , [BF] , [CG] sont les hauteurs. Démontrons
qu'elles sont concourantes. |
|
|
|
|
|
Par chaque sommet, tracez la parallèle au côté opposé.Vous obtenez le triangle MNP.Le quadrilatère ACBP est un ………………………………………(Expliquez pourquoi oralement).Donc, grâce à la
« propriété
10 » , BC = ……………………………….
De même ANCB est un ………………………………………………..Donc BC = ……………et par transitivité ……..=…………Donc A est le …………………. de [PN] .La droite (AE) est perpendiculaire à (BC) (car [AE] est une ……………..) et comme (BC) est parallèle à (PN), alors (AE) est …………………………………… à (PN) ,Donc (AE) est ……………………………de [PN] .On démontre de même que (BF) est médiatrice de ………. et (CG) médiatrice de ……………Puisque les médiatrices des côtés d'un triangle sont …………………………………………….alors (AE) , (BF) , (CG) sont …………………………………. .On dira alors : |
|
||
|
|
Théorème 25 :
Dans tout triangle , les hauteurs sont concourantes en un point
que l’on appelle l’orthocentre du triangle. |
|
||
|
|
|
|
||
|
|
CONSTRUCTION DES HAUTEURS D'UN TRIANGLE
|
|
||
|
|
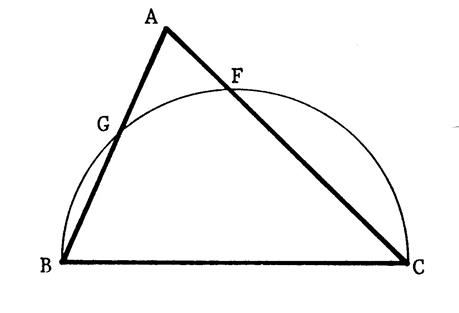
Voici ,ci-contre un triangle ABC.
On a tracé le cercle de diamètre [BC] qui
coupe (AB) en G et (AC) en F.
Tracez [BF] et [CG] .
Démontrez que [BF] et
[CG] sont hauteurs du triangle ABC.
|
|
|
|
|
|
·
(BF) et (CG) se coupent en H . Trace
(AH) qui coupe (BC) en E. Démontre que
est hauteur |
|
||
|
|
Activité : Tracez comme on vient de le faire les hauteurs des deux triangles
ci-dessous
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EXERCICES SUR LES HAUTEURS D'UN TRIANGLE.
|
|
|
|
|
|
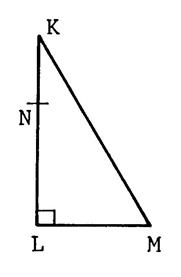
Exercice 1 :
KLM est un triangle rectangle en L. N est un point quelconque de (KL). Trace
par K la perpendiculaire à (MN) qui
coupe (MN) en P et (LM) en R. Démontre
que (RN) est perpendiculaire à (KM).
|
|
|
|
|
|
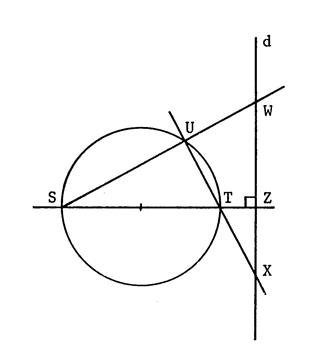
Exercice 2 :
On donne un cercle et [st] un de ses diamètres .
« d » est une
droite perpendiculaire à (ST).
« U » est un point
du cercle. (SU) coupe « d » en « W ».
(UT) coupe « d » en
« X » et (ST) coupe « d » en « Z ».
1°) Démontrez que (WT) est perpendiculaire à (SX).
2°) Démontrez que U,W,Z,T sont
sur un même cercle dont vous préciserez le centre.
3°) Trouvez quatre points de la figure situés sur un même cercle.
|
|
|
|
|
|
|
|
||
|
|
Fiche 3 :
Les Médianes : |
|
|
|
|
|
On appelle médiane d'un triangle le
segment joignant un sommet au milieu du côté
opposé. Par abus de langage "médiane" désigne aussi le support de ce segment. |
|
||
|
|
|
|
||
|
|
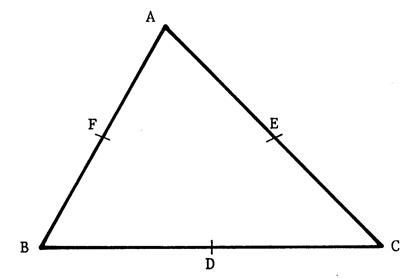
Voici, ci-contre , un triangle « ABC ». Tracez
les médianes [BE] et
[CF] . Ces deux segments ont un point commun (on
peut le démontrer). Appelons-le « G ». Nous
allons démontrer que la médiane [AD]
passe aussi par G. |
|
|
|
|
|
Appelons « M » le milieu de [bg] et N le milieu de [CG].
Dans le triangle « ABC », par hypothèse « F » est milieu de [AB] et « E » est milieu de [ AC ]
Donc, grâce aux théorèmes « 2 » et
« 3 », (EF) est ………………………… à (BC)
et FE = ……..BC.
Dans le triangle BGC,
« M » est le milieu de [BG] et
« N » est le milieu de [CG] , donc,
grâce
aux théorèmes « 2 » et « 3 », (MN) est …………………… à (BC) et MN = ….
Grâce à la transitivité du parallélisme, (EF) est …………………………………………..
Grâce à la transitivité de
l'égalité EF = …………………………………………
Le quadrilatère
convexe « FENM » a une
paire de côtés parallèles et de même longueur, grâce à la « propriété
15 » ce quadrilatère est un …………….
Grâce à la « propriété 8 »,
ses diagonales se coupent en leur milieu,
donc,
« G » est le milieu de ………… et de …………….
donc,
GF = GN et comme « N » est
le milieu de [CG], « GN =
NC » donc « CG = —CF »
|
|
||
|
|
Théorème :
Dans tout triangle
, les médianes sont concourantes en un point appelé « centre de
gravité » du triangle.
Ce point est situé aux deux tiers de la longueur de chaque médiane à partir du sommet. |
|
||
|
|
|
|
||
|
|
Activités :
|
|
||
|
|
Exercice
1 : On vous donne, ci-contre, un triangle ABC et M milieu de [AB]. Placez
sur [MC un point
« D » tel que « CD = 2 MC » . (AC)
coupe (BD) en E et
(BC) coupe (AD)
en « F ». Démontrez que « E » est
le milieu de [BD] et « F » le milieu de [AD]. |
|
|
|
|
|
Exercice
2 « ABCD » est un parallélogramme
de centre « 0 ». « M » est un point extérieur au parallélogramme. Démontrez que les triangles « AMC » et
« BMD » ont même centre de gravité. |
|
||
|
|
|
|
|
|
|
Fiche 4 : Les
Bissectrices
|
Info
++@ +++
|
|
|
|
|
|
|
|
|
Voici un triangle « ABC » quelconque.
Tracez les bissectrices de
|
|
|
|
|
Grâce au théorème 23, on peut dire
que :
« I » étant situé sur la bissectrice de
|
|
|
|
|
Théorème 27
Les bissectrices d’un
triangle sont concourantes en un point qui est le centre du cercle
inscrit dans le triangle.
|
|
|
|
|
|
|
|
|
|
Activité : Exercice.
|
|
|
|
|
1°)Sur la droite
ci-dessous , construisez un triangle
« DEF » tel que (en mm) DE = 102, DF = 48, FE » 90.
Le côté [ D E] est déjà
placé.
Déterminez le centre 0 du cercle inscrit dans le
triangle DEF et tracez ce cercle.
Placez les points
« G », « H », « K » projetés orthogonaux
de « O » respectivement sur (EF),(FD),(DE).
|
|
|
|
|
|
|
|
|
|
(suite)
2°) Démontrez
que DEF est un triangle rectangle (fais les calculs sur une autre
feuille).
3°) Démontrez
oralement que FGOH est un carré.
4°) Démontrez
oralement que DK = DH , KE = EG , HF = GF = R
(R : rayon du cercle inscrit)
5°) Vous allés
calculer le rayon « R » du cercle inscrit. (Vous contrôlerez sur le dessin)
|
|
|
|
|
Mise en équation :
|
|
|
|
|
« K » étant un point de [ DE] , alors « DE = DK + KE » et puisque « DK = DH » et « KE = EG » alors
DE =……..+ ………
« DF
= DH + HF » donc « DH = DF
………………. Or, « DF = 48 » et
« HF = R » donc DH
=……….+ ……… « EF = EG +………. » donc « EG =…………. » Or,
« EF= ………… » et ………………….donc « EG =………………………. »
Sachant que
« DE = 102 », l'égalité
« DE = DH + EG »
peut s'écrire : 102 = 48 - R
+ ………….
· Vous êtes en présence d'une
équation. A vous de la résoudre.
|
|
|
|
|
|
|
|||||
|
|
Fiche 5 : Reconnaître un
triangle isocèle.
|
Info ++ @
++sur le triangle isocèle++
|
|
||||
|
|
Vous avez vu en 5° (et on l'a rappelé dans les
fiches 10 )
que :
|
|
|||||
|
|
Rappel :
Dans tout triangle isocèle,
la hauteur principale, la bissectrice principale, la médiane principale et la médiatrice de la base ont leurs supports confondus (avec
l'axe de symétrie du triangle).
|
|
|
||||
|
|
Démontrez « verbalement » les propriétés suivantes relatives à un
triangle.
1°) Si la médiatrice d'un côté est aussi bissectrice de l'angle
opposé alors le triangle est isocèle.
2°) Si la médiatrice
d'un côté est aussi hauteur, alors le triangle est isocèle.
3° )
Si la médiatrice d'un côté est aussi médiane, alors le triangle est isocèle. 4°) Si une hauteur est aussi médiane, alors
le triangle est isocèle. 5°) Si
la bissectrice d'un angle est aussi hauteur, alors le triangle est isocèle. |
|
|||||
|
|
Nous allons démontrer ensemble la 6° propriété :
6°) Si dans un triangle la
bissectrice d'un angle est aussi
médiane, alors le triangle est isocèle.
( voir le dessin ci - dessus )
|
|
|||||
|
|
Hypothèse :
[AM] médiane
[AM bissectrice de
|
Conclusion :
BAC est
isocèle (AB = AC)
|
|
|
|||
|
|
• Appelons « E » le symétrique de
« A » par rapport à « M » ;
par définition,
« M » est alors le milieu de …………………….
Par hypothèse,
[AM] est médiane donc M est le milieu de ……………..
alors, grâce à la propriété 12, « ABEC » est un
………………………….
Donc, grâce à la
propriété 10 : AB
=…………………………………
et par définition
(AB) est parallèle à ……………………………….
En considérant ces deux
parallèles et la sécante (AE) , On peut dire que les angles
[AM
étant bissectrice de donc, grâce à la
propriété 26, le triangle « ACE » est …………………………..
Donc, par
définition,
« AC = EC » et comme « AB = EC » alors « AB =…………. ».
donc, par définition, le triangle « BAC » est ……………………………. |
|
|||||
|
|
|
|
|||||
|
|
· En regroupant les 6 propriétés, on énoncera alors :
|
|
|||||
|
|
Théorème 28 :
|
|
|||||
|
|
|
|
|||||
|
|
Activité :
Exercice
On donne un segment
|
|
|
||||
|
|
|
|
|
|
|
Fiche 6 : Le triangle
équilatéral.
|
Info
++++@+le triangle équilatéral+++
|
|
|
|
|
|
|
|
|
Ci-contre ,
on vous donne « ABC » , un triangle équilatéral.
Activités :
1°) Trace
son cercle inscrit et son cercle
circonscrit.
Expliquez
pourquoi (verbalement) ces cercles
sont concentriques.
2°) Soit « O » le
centre de ces cercles, tracez (AO). (AO) coupe (BC) en « M ».
3°) Quelle est la position de « O »
sur [ AM
] ?
4°) Soit « R » le rayon du cercle circonscrit et
« r » le rayon du
cercle inscrit. Quelle relation
existe-t-il entre « R » et « r » ? |
|
|
|
|
|
|
|
|
|
Fiche 7 : Activités –
Exercices.
|
( pas de corrigé fait …)
|
|
|
|
|
|
|
|
|
Exercice 1 ABC est un triangle quelconque. M est le milieu de E est le symétrique de A par rapport à M. F est le symétrique de C par rapport à B. Démontrez que B est le centre de gravité du triangle AFE. |
|
|
|
|
Exercice 2 MNPR est un parallélogramme de centre 0. G est le milieu de [MN] . (RG) coupe (MP) en H. (NH) coupe (MR) en K. Démontrez que K est le milieu de | MR] |
|
|
|
|
Exercice 3 ABC est un triangle quelconque. D est le milieu de [BC] . E le milieu de [CA] , F le milieu de [AB] . Démontrez que les triangles ABC et DEF ont le même centre de gravité. |
|
|
|
|
Exercice 4 ABCD est un losange tel
que La perpendiculaire à (AD) passant par B coupe (AC) en E. La perpendiculaire à
(BC) passant par D coupe (AC) en F. |
|
|
|
|
Exercice 5 ABC est un triangle tel que BC = 2 AC . [AM] est médiane. E est le milieu de [CM] et F le milieu de [AC] . (AE) et (MF) se coupent en O . 1°) Démontrez que AOM est un triangle isocèle. 2°)
Démontrez que [AM est
bissectrice de
|
|
|
|
|
Exercice 6 ABC est un triangle rectangle
en A
de hauteur [AH] .
La
bissectrice de
|
|
|
|
|
Exercice 7
On donne
un cercle de diamètre [AB] et un point D quelconque sur
le cercle (D
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Fiche 8 : Propriété des
points intérieurs à un triangle
équilatéral.
|
Info +++@ +++++
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
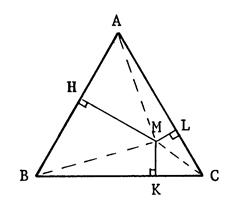
Ci-dessous :
Voici un triangle équilatéral. Tracez ses hauteurs
[AA'] , [BB\] , [CC’l .
Mesurez ces segments vous
trouvez :……………………………mm.
(Expliquez pourquoi, oralement, ils ont la même longueur). |
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
· Choisissez
un point « M »
quelconque à l'intérieur du triangle.
Projetez orthogonalement ce point sur les côtés du
triangle.
Mesurez (en mm) la somme des
distances de « M » aux côtés
du triangle et faîtes -en la somme.
Vous trouvez :…….+ …….. + ………..=……….
Choisissez un autre point
« N » à l'intérieur du
triangle et faites comme vous l'avez
fait pour « M ».
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
·
Nous
allons faire une démonstration pour prouver ce que vous venez
de constater.
Appelons « H », « K » , « L »
les projetés orthogonaux de « M » respectivement sur
(AB),(BC),(ÇA). Appelons " h " la
longueur de chaque hauteur et "a" le côté du triangle
« ABC ». Calculons l'aire du triangle
« ABC » de deux façons différentes.
|
|
|||||||||||||||||||||
|
|
Première façon :
|
|
|||||||||||||||||||||
|
|
Deuxième
façon :
|
|
|||||||||||||||||||||
|
|
Découpons le triangle ABC en
trois triangles :
AMB , BMC , CMA.
On a alors : Aire(ABC) = Aire(AMB) + Aire(BMC) + Aire(CMA)
Pour le triangle AMB (par
exemple), « BA = a » et la hauteur correspondante est
………………………………..
Donc Aire(AMB)
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
FICHE 9 : Application aux
statistiques. (exploitation de données
statistiques).
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
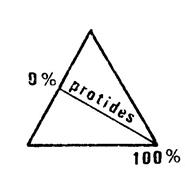
La propriété de la précédente ( Fiche 7 ) est utilisée pour la représentation
graphique de situations comportant trois
données dont la somme est constante.
Nous allons utiliser cette méthode pour comparer la
composition des aliments
Vous savez
que les aliments sont composés essentiellement (en enlevant l'eau) de glucides, lipides et protides, (les sels
minéraux et les vitamines ayant une masse négligeable).
Exemple : Pour 100g de lait
de vache, il y a 5g de glucides, 3,7g de lipides, 3,5g de protides, environ 50mg de sels minéraux et vitamines. Le reste est de l'eau.
Masse totale des trois
constituants principaux : 5 g + 3,7 g + 3,5 g = 12,2 g
Calculs des
pourcentages : |
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
Pourcentage de glucides
|
Pourcentage de lipides
|
Pourcentage de protides
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
Résultat :
|
|
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
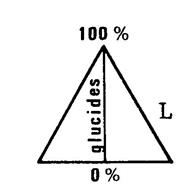
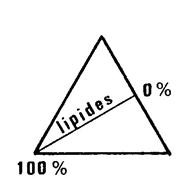
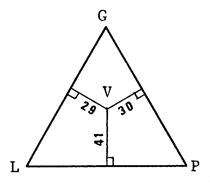
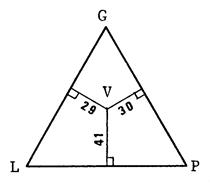
Le triangle « GLP »
est équilatéral et sa hauteur mesure 100mm.
Dans ce triangle, on a placé
le point « V » représentant
le lait La distance de « V » à (LP) représente le pourcentage de
glucides La distance de « V »
à (PG) représente le pourcentage de lipides. La distance de « V »
à (GL) représente le pourcentage de protides.
Le total de ces trois
distances est égal à ……………………………….
Vérifiez que « V »
est bien placé dans le triangle ci-dessous.
Après avoir fait les mesures nécessaires sur le
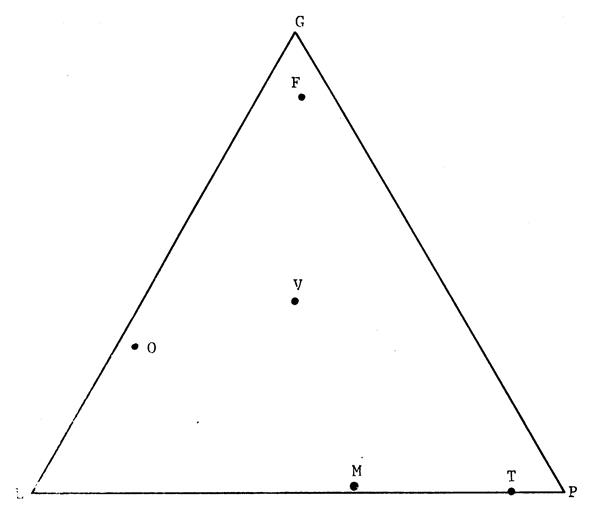
triangle, complétez le tableau donnant la composition des différents aliments représentés par les points
« M » , « F » , « O »
, « T » .
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
Aliments
|
Points
|
Glucides
|
Lipides
|
Protides
|
|
||||||||||||||||
Lait
|
V
|
41%
|
30%
|
29%
|
|||||||||||||||||||
Mouton
|
M
|
|
|
|
|||||||||||||||||||
Fraise
|
F
|
|
|
|
|||||||||||||||||||
Olive
|
O
|
|
|
|
|||||||||||||||||||
Truite
|
T
|
|
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
Placez les points correspondant aux aliments
désignés dans le tableau ci-dessous
Commencez par calculer le pourcentage des différents constituants.
(Prenez
modèle sur ce qui a été fait pour le lait).
Vous pouvez faire un certain nombre de remarques
(verbalement).
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
Aliments
|
Chocolat
|
Amandes
|
Gruyère
|
Haricots
|
Yaourt
|
Crème
|
|
|||||||||||||||
Points .
|
C
|
A
|
R
|
H
|
Y
|
K
|
|||||||||||||||||
Glucides
|
65 g
|
%
|
14 g
|
%
|
0 g
|
%
|
7,4 g
|
%
|
4 g
|
%
|
4 g
|
%
|
|||||||||||
Lipides
|
22 g
|
%
|
53 g
|
%
|
33 g
|
%
|
0,2 g
|
%
|
1,5 g
|
%
|
25 g
|
%
|
|||||||||||
Protides
|
7 g
|
%
|
21 g
|
%
|
37 g
|
%
|
2,4 g
|
%
|
3,4g
|
%
|
3,5 g
|
%
|
|||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
Faire toutes les
fiches. ( fini
le 9 /12 / 2012 )
|
|
|||||||||||||||||||||