3ème collège: les angles inscrits dans un cercle.

	Vers le programme de troisième.	Classe de troisième .

Pré requis:
Le cercle
Angles et rapporteur

ENVIRONNEMENT du dossier:

Niveau 5 et 4

Index : warmaths

Objectif précédent :

1°) l’angle et sa mesure .

2°) Angle au centre , angles inscrits.

Objectif suivant : mesure des arcs d’un angle.

Liste des cours sur les angles.

Fiches : Les ANGLES INSCRITS dans un cercle.


	Fiche 1 : Triangle rectangle.
	Fiche 2 : Constructions .
	Fiche 3 : Problème.
	Fiche 4 : Angle au centre – Angle inscrits.

		Devoir auto formatif
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

	Fiche 1 : Triangle rectangle.	Info ++@ ++++
	Vous avez vu en 4^ème le théorème suivant :
	Théorème : Si un triangle est rectangle, alors son cercle circonscrit a pour centre le milieu de l’hypoténuse. L’ Hypoténuse est alors diamètre du cercle.
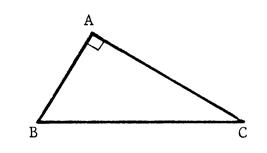
	Activité : Tracez le cercle circonscrit au triangle rectangle « ABC » (ci-contre), « O » étant le centre de ce cercle , tracez la médiane [AO ]. Vous retrouvez un autre théorème étudié en 4^ème .
	Théorème : Dans un triangle rectangle , la longueur de la médiane relative à l’hypoténuse est égale à la moitié de la longueur de l’hypoténuse.

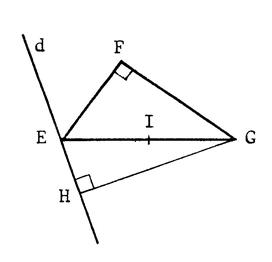
	Activité n°2 : « EFG » est un triangle rectangle en « F ». « I » est le milieu de [ GE ]. « d » est une droite passant par « E », distincte de ( EF ) et ( EG ). « H » est le projeté orthogonal de « G » sur « d ». Démontrez que « I » est situé sur la médiatrice de [FH]
	Théorèmes réciproques des théorèmes précédents.
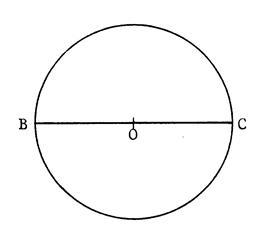
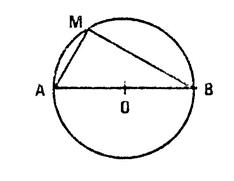
	Choisissez un point « A » quelconque sur le cercle ci-contre et tracez le triangle « BAC ». Contrôlez que est droite.
	Théorème : Etant donné un cercle et [BC] un de ses diamètres , si « A » est un point quelconque du cercle , ( A B ; A C ) alors le triangle « BAC » est un triangle rectangle « A ».
	Et voici un théorème qui en découle :
	Théorème : Si dans un triangle , la longueur d’une médiane est la moitié de la longueur du côté correspondant alors le triangle est …………………et le côté considéré est …………………………..

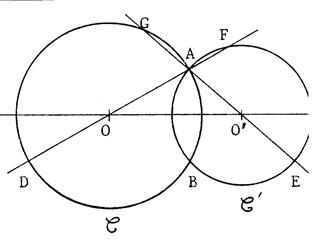
	Activité : Deux cercles « C » et « C’ » de centres respectifs « O » et « O’ » se coupent en «A » et « B ». ( AO ) recoupe le cercle « C » en « D » et le cercle « C’ » en « F ». ( A O ‘) recoupe le cercle « C’ » en « E » et le cercle « C » en « G ». 1°) Démontrez que « D » , « B » , « E » sont alignés ( tracez [AB] ). 2°) Démontrez que « D » , « G » , « F » , « E » sont sur un même cercle. ( Tracez ce cercle )

	Fiche 2 : Constructions .
	Problème 1 : Construisez un triangle « ABC » rectangle en « A » dont l’hypoténuse est le segment [ BC] ci-contre et dont la longueur de la hauteur est 25 mm. Indication : Le triangle cherché est inscrit dans le cercle de diamètre ……………..
	Problème 2 : Dans les deux cas ci-dessous , on donne un triangle « ABC ». Tracez le demi-cercle de diamètre [ BC] . Il coupe ( AB ) en « E » et (AC ) en « F ». Tracez (BF ) et ( CE ) . Elles se coupent en « H ». Tracez ( AH ) qui coupe ( BC ) en « K ». Démontrez ( verbalement) que [ BF] [ CE] [ AK] sont les hauteurs du triangle « ABC ». ( « H » s’appelle ………………………………………….du triangle « ABC »)

Fiche 3 : Problème.

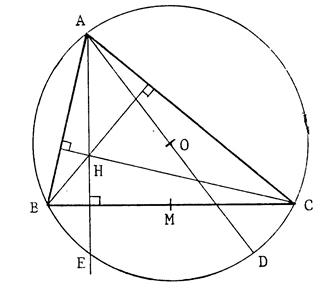
« O » est le centre du cercle circonscrit au triangle « ABC ».

« H » est l’orthocentre du triangle « ABC ».

( AH ) recoupe le cercle en « E ».

[ AD] est diamètre du cercle. « M » est le milieu de [ BF] .

1°) Démontrez que ( BH ) et (CD) sont parallèles ainsi que (CH )et (BD).

2°) Démontrez que « M » est le milieu de [ HD] .

3°) Démontrez que ( ED ) et (BC) sont parallèles.

4°) Démontrez que « E » est le symétrique de « H » par rapport à (BC ).

	Fiche 4 : Angle au centre – Angle inscrits.
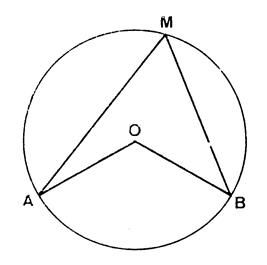
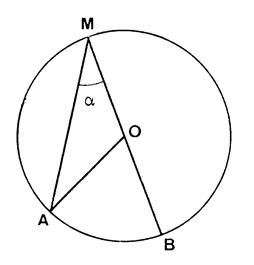
	Vocabulaire : Ci-contre , un cercle de centre « O ». « A » et « B » sont deux points de ce cercle. · L’angle a son sommet au centre du cercle. est appelé « angle au centre ». On dit qu’il intercepte l’arc . · « M » étant un point quelconque du cercle , ( M A et M B ) , l’angle est appelé « angle inscrit dans le cercle » Son sommet est sur le cercle et ses côtés coupent le cercle en « A » et « B ». On dit qu’il intercepte l’arc
	Exercice : Sur la figure ci-dessus , placez des points qu’on appellera « C » , « D » et « E » tel que , , soient des angles inscrits interceptant le même arc . Mesurez , , , . Que constatez vous ? ……………………………………………………………. Mesurez l’angle au centre . Que constatez-vous ? …………………………………………………………… C’est ce que nous allons démontrer ci-dessous.
	Relation entre un angle inscrit et l’angle au centre interceptant le même arc.
	Cas particulier : est un angle inscrit tel que [ MB ] soit un diamètre. Comparons et . Appelons l’angle . [OA ] et [OM ] sont des rayons, donc le triangle « AOM » est isocèle , donc Dans le triangle AOM , = 180° - ( ………+ ……..) C'est-à-dire , = 180° - 2 ou encore : 2 = 180 ° -
	Puisque est plat , et sont …………………………………………………………. Donc : - donc On peut écrire = ………
	Cas général : est un angle inscrit quelconque de l’angle au centre interceptant le même arc . Traçons le diamètre [ MN ] ; Il y a deux cas de figure possibles.

	= + = 2 AMN + 2 …….. = 2 ( …… + ………) = 2 ou = …..				= - = 2 AMN - 2 …….. = 2 ( …… - ………) = 2 ou = …..

	Théorème : Tout angle inscrit est égal à la ……………………………….. ;de l’angle au centre qui intercepte le même arc. Si deux angles inscrits interceptent le même arc alors ils sont ………………………

	Cas particulier : Quand [ AB ] est un diamètre , AOB = …………………° ; donc AMB = ……..° On retrouve le 3^ème théorème de la fiche 1.

	Fiche 5 Exercices.
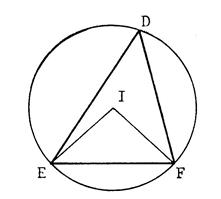
	Exercice 1 : On donne un triangle « DEF » et son cercle circonscrit de centre « I » . = 57° , = 75 ° , Calculez

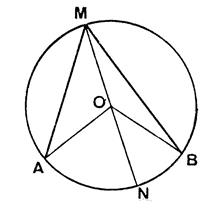
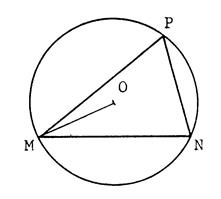
	Exercice 2 : MNP est un triangle dont les angles sont aigus. « O » est le centre de son cercle circonscrit. Sachant que = 25 ° , calculez .
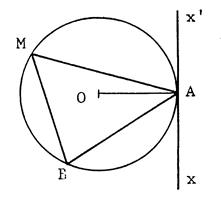
	Exercice 3 : On donne un cercle et un point « M » extérieur au cercle. Une droite passant par « M » coupe le cercle en « A » et « B » ( « A » entre « M » et « B » ) Une autre droite passant par « M » coupe le cercle en « C » et « D » ( « C » entre « M » et « D » ) (BC ) et (AD ) se coupent en « P » . = 76° , = 34 °. Calculez : , , , .

	Exercice 4 : un angle inscrit dans un cercle de centre de « O ». « » est la tangente en « A » au cercle . ( voir ci-contre ). Démontrez que =

	Exercice 5 : On donne un cercle de centre « O » et de diamètre [ CE ]. « A » et « B » sont deux points du cercle de part et d’autre de (CE) et tels que = 90° et = 60° Calculer les angles du triangle ABC.

	Exercice 6: « O » est le centre du cercle circonscrit au triangle ABC , [ AK ] est hauteur . (AK) recoupe le cercle en « E », [ AD ] est le diamètre. 1° ) Démontrez que les triangles ABK et ADC ont leurs angles respectivement égaux. 2°) ( BD ) et (EC ) se coupent en « F ». Démontrez que BFC est un triangle isocèle.
	Fini le 20/1/15