CORRIGE : ANGLES INSCRITS.

CONTROLE:

1° ) Qu’appelle t – on « angle au centre » ?

Définition : Un angle au centre est un angle qui a son sommet au centre d’un cercle.

2° ) Qu’appelle t – on « angle inscrit » ?

On appelle « angle inscrit » dans un cercle un angle qui a son sommet sur un cercle et dont les cotés sont sécants ou tangents à ce cercle .

3° ) Compléter les phrases suivantes :

un angle inscrit dans un demi cercle est un angle droit.

Deux angles inscrits dans un même cercle et interceptant le même arc sont égaux.

EVALUATION:

SERIE 1:

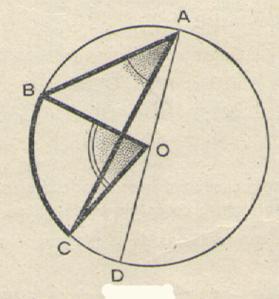
Activité 1: Dans quel cas sommes nous ? le centre du cercle est à l’extérieur de l’angle inscrit.
On donne le diamètre AOD. Compléter les phrases suivantes: L’angle BAD = l’angle BOD divisé par 2. L’angle CAD = l’angle COD divisé par 2 . L’angle BAC = l’angle BAD – l’angle CAD = ( l’angle BOD – l’angle COD) divisé par 2 . L’angle BAC = l’angle BOC divisé par 2.

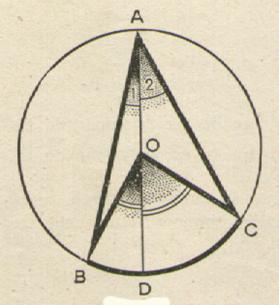
Activité 2 : compléter les phrases. Quel est le cas étudié ? le centre du cercle est à l’intérieur de l’angle inscrit.
L’angle A1 est égal à l’angle BOD divisé par deux . L’angle A2 est égal à l’angle DOC divisé par deux . L’angle BAC est à la somme des angles A1 + A2 qui est égal à l’angle BOD divisé par deux plus l’angle DOC divisé par deux . Ainsi l’angle BAC est égal à l’angle BOC divisé par deux .

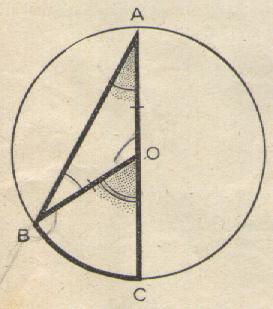
Activité 3 : Quel est le cas étudié? l’un des cotés de l’angle inscrit passe par le centre du cercle
A quel angle est égal l'angle BAC ? l’angle BAC est égal à l’angle BOC divisé par deux.

2°) Un angle au centre a pour mesure 108° ; quelle est la mesure d'un angle inscrit qui intercepte le même arc?

3°) Un arc AB vaut 1/10 de la circonférence, les tangentes au disque en A et B se coupent en C .

a)quelle est la mesure de l'angle au centre correspondant?

b)Calculer la valeur des angles du triangle ABC .