Pré requis :

Fonctions présentation
Devoir précédent

 

CORRIGE :  LES FONCTIONS  …devoir sommatif……

 

 

PARTIE 1 :

I  )        TRADUIRE :

  a)  f : N R

            x   2, 5 x 

il y a fonction de l ‘ensemble N(naturels) vers l’ensemble R ( Réels) où « x » à pour image « 2,5 x »

b )  f :  N   D       

             x   3x +2 

il y a fonction de l ‘ensemble N(naturels) vers l’ensemble D ( décimaux ) où « x » à pour image « 3 x+2 »

 

c)   f :  R   R

           x   2x² +3x -1 

il y a fonction de l ‘ensemble R(réels) vers l’ensemble R ( Réels) où « x » à pour image « 2x² +3x -1 

»

 

II ) citer les différentes représentations d’une fonction.

 

      pour chacune d’elles , préciser  ou donner  un modèle .

équation	Forme  : y =   f(x)
Représentation  graphique	On appelle « représentation graphique » L’ensemble des couples ( x ; y ) ,  où chaque couple ( x ; y )  représente les coordonnées d’ un point  où « x » est l’abscisse et « y » l’ordonnée dans un repère cartésien.
Graphe	On appellera :    graphe d ' une fonction de "D"    vers   "A"     l ' ensemble des couples ( x ; y ) où  "x" est un élément de  "D" et y son image dans  "A" .  ( D désigne l 'ensemble de départ et A l ' ensemble d ' arrivée )
Tableau de variation

 

Un tableau de variation est le représentant d ' une fonction si à une valeur de (x) correspond une seule ( au plus ) valeur de "y".

Il est de la forme:

 

y = Relation en f (x)		A	B	C	D	E
	x	x A	xB	xC   ; xD ;   xE :    « ligne des abscisses »
	y	yA	yB	yC ; yD ;  yE   ; « ligne des ordonnées »

Où:

  Dans la représentation graphique  le point A  a pour  coordonnées :

L ' abscisse  : le nombre x_A

L ' ordonnée : le nombre y_A

PARTIE 2 

 

I  )  Soit  Trois  équations :

y₁ = 2 x

y ₂ = -3x + 4

y₃ = 2x² -x +0,5

de quelle forme sont - elles ?

II )Pour faire la représentation graphique des fonctions suivantes  tracez  un repère cartésien  orthogonal sur le papier millimétré ;        prendre   lg [OI] =2 cm ; lg [OJ] =1cm ) ;

          Avec  -5 < x < 5  et     - 4 < y < 14

A  ) Pour l’équation : y₃ = 2x² - x + 0,5

  a)  construire le  tableau de variation de la fonction  f₃  (x) ; prendre des valeurs entières  entres [ -3 ; 3  ]  

 

x	-3	-2	-1	0	1	2	3
y	21,5	10,5	3,5	0,5	1,5	6,5	15,5

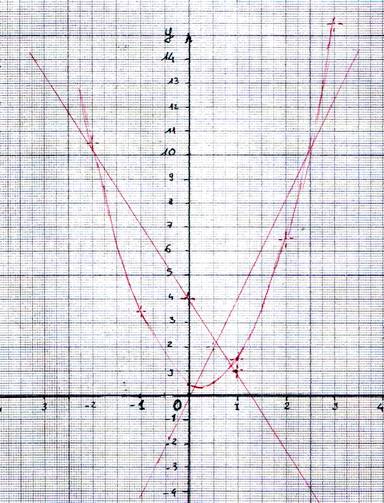
  b ) faire la représentation graphique. dans un repère cartésien  orthogonal ,de  f₃  (x)   

 B   )  Pour l’équation : y ₂ = -3x + 4

              faire la représentation graphique. dans un repère cartésien  orthogonal ,de  f₂  (x)   

  E  ) Pour l’équation :  y₁ = 2 x

    a )  Donner le graphe de la fonction  f₁  (x). Pour des valeurs entières  ] -3 ; 4].

(-2 ; -4 ) ; ( -1 ; -2 ) ; (0 ; 0 ) ; (1 ;2 ) ; ( 2 ; 4 ) ;(3 ;6 ) ;( 4 ;8 )

    b ) Faire la représentation graphique de f₁  (x).

E) Analyse de la représentation graphique des trois fonctions.

 

 

 

Donner les valeurs des points d’intersections (les relever sur le graphique)

	f1  (x)	f2  (x)	f3  (x)
f1  (x)
f2 (x)
f3  (x)