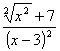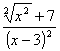CORRIGE : LES FONCTIONS
…Pré requis
1) On
donne l’équation y = 3,5 x
; calculer :
|
si x = 2 |
alors y = 7 |
|
si x = -2 |
alors y = -7 |
|
si x = 3/7 |
alors y =10,5 /7 ; = 1,5 |
|
si x = 5 |
alors y = 17,5 |
|
si x = 3/4 |
alors y = 2,625 |
2) On
donne l’équation de la forme : y = a x ; calculer :
|
si x = 4 |
et y = 6 |
alors a = 1,5 |
|
si x =-2,7 |
et y = 3,2 |
alors a = - 3,2
/2,7 ; -1,1851852 |
3) Calculer : Savoir trouver la valeur de
« y » si l’on donne une valeur
à «a ; x ; b » dans les cas suivants :
(Remplir le tableau
suivant)
|
Forme y = ax +b |
|
|
a = |
x = |
b = |
y = ax + b |
Résultat y = |
|
3 |
+2 |
+2 |
|
8 |
|
-1,5 |
-2 |
+3 |
|
+6 |
|
+ 2 / 3 |
3 |
1,5 |
|
3,5 |
|
CALCULS |
||
|
Soit l'équation: |
Pour une valeur de "x" donnée |
Calculer « y » |
|
équation |
Si x = 2 |
Alors y = ( corrigé : ) |
|
Y = 3x |
|
6 |
|
Y = |
|
-4/7 |
|
Y =3x+5 |
|
11 |
|
Y = |
|
10/7 |
|
Y =3x2 |
|
12 |
|
Y = |
|
1 |
|
Y =3x2+5x ; |
|
22 |
|
Y = |
|
15 |
|
Y =3x2+5x +1 |
|
23 |
|
Y = |
|
17 |
|
Y = |
|
1,414 |
|
Y = |
|
9 |
4 ) résoudre les équations du premier degré suivantes :
|
|
|
|
A ) 45 = 0,5 x |
= 90 |
|
B ) 18 = |
36 |
|
C ) 16= x + 0,5 |
15,5 |
|
D ) - 4,6 = 2,5 x + 1,3 |
-2,36 |
|
E ) 2,4 = |
-1,8 |
|
F ) 1,6 = -2 ,9 x |
- 0,551 |
5°) Calculer « y » pour les valeurs de « x »
données :
|
|
||||||
|
« x » ► |
( - 3,5) |
( - 2) |
( -1) |
0 |
( +1) |
( + 3) |
|
Y = 3x |
|
|
|
|
|
|
|
Y = |
(-1) |
4 / 7 |
2/7 |
O |
-2/7 |
- 6 / 7 |
|
Y =3x+5 |
-5,5 |
-1 |
+2 |
5 |
+8 |
+14 |
|
Y = |
+1 |
4/7 + 14/7 = 18/7 |
+ 16/7 |
+ 2 |
+ 12/7 |
+ 8 /7 |
|
Y =3x2; |
36,75 |
+12 |
+ 3 |
0 |
+3 |
+ 27 |
|
Y = |
2,625 |
+1 |
¼ = 0,25 |
0 |
¼ = 0,25 |
9/4 = 2,25 |
|
Y =3x2+5x
; |
|
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
|
Y =3x2+5x
+1 |
|
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
|
Y = |
|
|
|
|
|
|
6°) Soit l’expression algébrique « b²
- 4 ac » : (
SOS application)
On donne
les valeurs de « a » ; « b » et « c » ,
calculer « b² - 4 ac »
|
|
« a » |
« b » |
« c » |
« b² - 4 ac » |
|
1 |
2 |
3 |
5 |
|
|
2 |
( +1) |
( - 2) |
( +2) |
|
|
3 |
( + 0,5) |
( - 2 , 5) |
( -1) |
|
|
4 |
( + 4) |
( +2 ) |
( +1) |
|
|
5 |
0,75 |
0,5 |
3 |
|
|
6 |
( - 3 ) |
( + 4) |
( - 2) |
|
7°) Soit l’expression algébrique
« a x² + bx + c » ; on en tire l’expression « b² - 4 ac » :
Observer
l’expression « a x² + b x +
c » , en extraire les valeurs de « a » ;
« b » et « c » , calculer « b² - 4 ac »
|
|
a x² + b x + c |
« a » |
« b » |
« c » |
« b² - 4 ac » |
|
exemple |
3 x² + 5x - 4 |
( + 3) |
( +5) |
(-4) |
( + 5)² - [
4 ( +3) (- 5)]= 25 +60 = 85 |
|
1 |
-3 x² + 5x + 4 |
|
|
|
|
|
2 |
0,5 x² - 2x +1 |
|
|
|
|
|
3 |
x ² - x
+ 2 |
|
|
|
|
|
4 |
2 x² + 3 x + 2 |
|
|
|
|
|
5 |
- x² - x + 3 |
|
|
|
|
|
6 |
|
|
|
|
|