Tous niveaux    Niveau V

DOSSIER : FONCTIONS ( généralités)  /  Objectif cours 37

Pré requis :

Pré requis :Calculs de couples de nombres
Repère cartésien
Fonction et application

ENVIRONNEMENT du dossier

INDEX   warmaths

Objectif précédent : Présentation

Objectif suivant : La représentation graphique

1°) Tableau       2°)présentation

 

DOSSIER LES FONCTIONS  « généralités » … :  le  GRAPHE

 

	1°) Définition d’  un graphe ?
	2°) Représentation symbolique mathématique d' un graphe .
	3°) Comment obtenir un graphe ?
	4 )  Graphe et représentation graphique :

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

COURS

 

1°)   Définition d’  un graphe ?

 

On peut obtenir  un graphe à partir d’une représentation graphique ou à partir  d’une équation mathématique ou à partir d’un tableau numérique :

 

 

  Obtention d’un 

1°)  GRAPHE d’une fonction L à partir d'un tableau

 

Prenons un exemple:

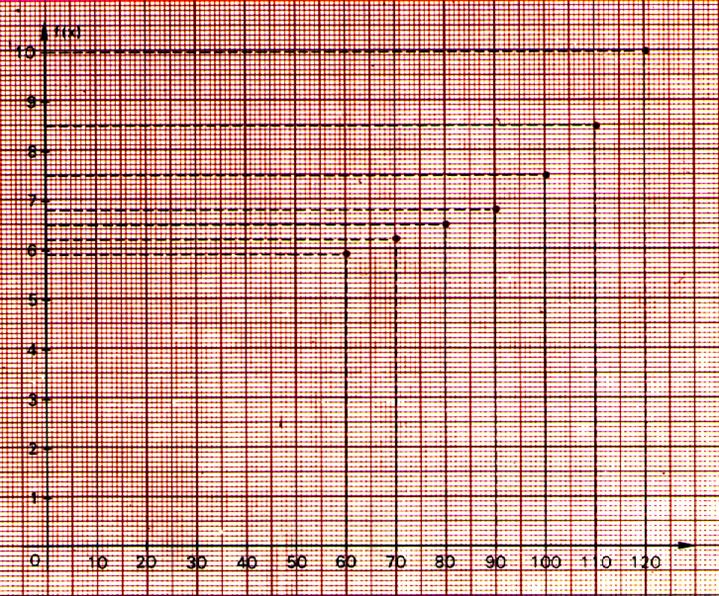
Un automobiliste a observé sa consommation de carburant à différentes vitesses .Il a obtenu le tableau suivant:

 

Vitesse en Km/h	60	70	80	90	100	110	120
Consommation en litre	5,9	6,2	6,5	6,8	7,5	8,5	10

 

Le tableau montre que 80 a pour image 6,5.On dit que le couple (80;6,5) est un élément du graphe de la fonction f.

 

 

On appellera :    graphe d ' une fonction de "D"    vers   "A"     l ' ensemble des couples ( x ; y ) où  "x" est un élément de  "D" et y son image dans  "A" .

 ( « D » désigne l 'ensemble de départ et « A » l ' ensemble d ' arrivée )

 

On désignera  par la lettre « G » l 'ensemble des éléments  regroupant le graphe d'une fonction « f »

 

 

D ' après l ' exemple: Le graphe de la fonction f est l 'ensemble « G » tel que:

 

G  = í(60;5,9) ; (70;6,2) ;(80;6,5);(90;6,8) ;(100;7,5) ; (110;8,5);(120;10)ý

 

En résumé : On appelle :    graphe d ' une fonction   l ' ensemble des couples  où  "" est un élément de l’ensemble de départ ;  «  » son image dans  l’ensemble  d’arrivée .

 

 

 Commentaires : les nombres dans les couples de points sont ordonnés. les couples  eux mêmes sont ordonnés.

 

 

2°)   Représentation symbolique mathématique d' un graphe .

 

G = í(";") ; (";") ;( ";");………. ý

 

 G     cette lettre majuscule qui désigne le graphe

 

( " ; " ) désigne un couple de nombres (placés dans un ordre précis) ;placés entre des accolades.

 

généralement dans la case de gauche se trouve "x"  et de droite "y" ; ce qui donne le couple

ce qui donne le graphe suivant :

G = í(x₁;y₁) ; (x₂;y₂) ;( x₃;y₃ );………. ý

 

 

Remarque: pour qu 'un graphe soit le graphe d ' une fonction il faut que les "x" n ' aient  au plus 1 valeur numérique. ( dit autrement : un "x" ne peut avoir deux valeurs )

 

3°)  Comment obtenir un graphe ?

 

Exercices Type: On donne la représentation graphique d ' une fonction f

 

On peut obtenir  un graphe à partir d’une représentation graphique ou à partir  d’une équation mathématique ou à partir d’un tableau numérique :

 

Exemple :

 

A )   Graphe et tableau :

 

Vitesse en Km/h	60	70	80	90	100	110	120
Consommation en litre	5,9	6,2	6,5	6,8	7,5	8,5	10

: Le graphe de la fonction f est l 'ensemble G tel que:

 

G  = í(60;5,9) ; (70;6,2) ;(80;6,5);(90;6,8) ;(100;7,5) ; (110;8,5);(120;10)ý

 

 

  Graphe et équation

 

Soit l’équation : y = 3x

Si nous affectons des valeurs à « x » (arbitrairement):  0 ; 0,5 ;2 ;3 ;6 ;9 ;120

 Le graphe de la fonction f est l 'ensemble G tel que:

 

G  = í(0;0 ) ; (0,5 ; 1,5 ) ;(2 ;6);(3; 9) ;( 6 ;18 ) ; (120 ; 360)ý

 

4 )  Graphe et représentation graphique :

 

                 Nous relevons dans la représentation graphique les coordonnées de certains points de la ligne tracée , ou de certains points isolés dans un repère cartésien.

Ces coordonnées forme des couples de points que l’on regroupera pour former un graphe.

 

 

D' après la représentation graphique . Le graphe de la fonction f est l 'ensemble G tel que:

G  = í(60;5,9) ; (70;6,2) ;(80;6,5);(90;6,8) ;(100;7,5) ; (110;8,5);(120;10)ý

 

Commentaire : on pourrait nommer chaque couple de valeurs  par une lettre majuscule ,tel que  par exemple : le point « A » à pour abscisse « 60 » et pour ordonnée « 5,9 » ; le point « B » : (70;6,2) ; le point « C » :(80;6,5) ; et ainsi de suite……….

 

 

TRAVAUX  AUTO - FORMATIFS

 

CONTROLE:

 

1°)  Quels sont les moyens d’obtenir un graphe ?

 

 

2°)  Qu ' appelle - t on "graphe" d' une fonction " ?

 

3°) Quelle est la représentation symbolique mathématique  d' un graphe  ?

 

 

EVALUATION:

 

1°)  Les graphes  G1 ; G2 ; G3 ; G4 ; G5 ; G6   représentent - ils chacun une fonction ? Justifier votre réponse .  (SOS COURS)

 

 

Graphes:	O ou N	justification
G 1 = í(3 ; 7 ) ; (5,2 ;) ;(4,8 ; 7 );()ý
G2  = í(1 ; 2) ; (2 ; 3) ;(3 ; 4 );(3 ; 5)ý
G3  = í(;) ; (;) ;( ;);(;1)ý
G4  = í(-3 ; 5 ) ; ( 3 ; 5 ) ;( 5 ; 4 );( 5 ; -2)ý
G5  = í(-4 ; ) ; (7 ; 8) ;( 9 ; 14 );( 7 ; 13)ý
G6  = í( 5 ; 5) ; ( 6 ; 6 ) ;( 7 ; 7);( 8 ; 8) ;( 9; 9 )ý

 

 

 

 

 

 

 

 

2°)  On donne la représentation graphique de la fonction « g » , donner son graphe.

 

 

 

 

3°)  On donne la représentation graphique de la fonction « f » , donner son graphe.