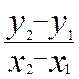la fonction affine ( classe de troisième)

	Classe de troisième

Résumé de cours : « fonction linéaire » et « fonction affine »		Voir programme classe de troisième.

DOC. : cliquer ici Professeur ; Formateur

DOC : formation individualisée soutien en ligne.

DOC : livre Elève .Cours interactifs - et travaux + corrigés.

TI ) Pré requis:

· Lecture : « fonction et application »	¥
· Les grandeurs proportionnelles ( liste des cours)	¥
· La fonction linéaire (généralement traité avant la fonction affine) · La fonction linéaire est une forme dérivée de la fonction affine : y = m x + p ( avec « p = 0 »	¥
· Droites et repérage	¥
· Les repère cartésiens	¥

II ) ENVIRONNEMENT du dossier :

Index warmaths.

AVANT :

Résumé sur les droites dans un repère.

2°) Fonction et application, affine .

COURS

APRES :

1°) Les droites croissante ; décroissante,..

2°)le parallélisme et la perpendicularité

Travaux : 3°) Fonction affine et application.

Complément d’Info :

Fonction affine : présentation

Fonction affine (niveau +++)

	III ) LECON n° 24 : LA FONCTION AFFINE .( classe 3^ème)
	CHAPITRES :
	I ) définition.
	II ) Propriétés :
	1°) Représentation graphique .
	2°) Proportionnalité des accroissements .
	3°) Détermination d’une application affine . ( recherche de « »)

IV) INFORMATIONS « formation leçon » :

Test

COURS

Travaux auto - formation.

Corrigé des travaux auto - formation.

	COURS
	Dans tout ce qui suit le plan est muni d’un repère ; noté aussi : ( ) Application affine :
	I ) définition
	« » et « » sont des nombres relatifs. Le procédé qui à tout nombre relatif « » associe le nombre « » est une application affine . « » et « » sont les coefficients de l’application affine . On note : ou on lit : par : donne ou la fonction « » où le nombre « » à pour image le nombre « »

	II ) Propriétés :
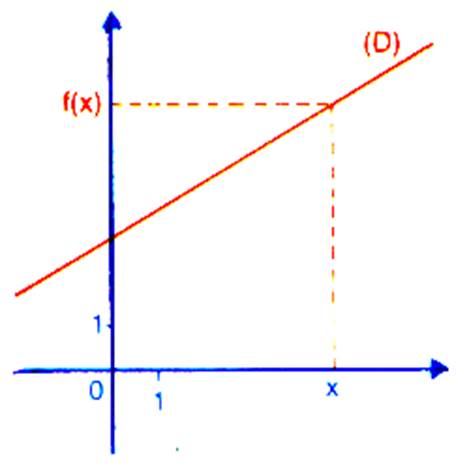
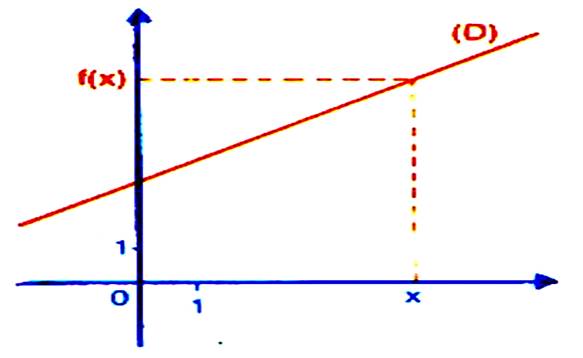
	1°) Représentation graphique : le plan est muni d’un repère ( O ;I ; J ) La représentation graphique de l’application affine « » définie par est une droite qui à pour équation « » . Pour que cette fonction soit une application ; cette droite n’est jamais parallèle à l’axe des ordonnées ( info plus ? ? ? ; cliquer ici )
	La fonction » » est définie par : la droite (D) a pour équation :
	¤Dans tous les cas le point appartient à la droite qui représente « ». C’est pourquoi « » est parfois appelé « ordonnée à l’origine » . ¤ Si ; (D) passe par O ( voir :fonction linéaire) si ; ( D ) est parallèle à l’axe des abscisses . Toute droite non parallèle à l’axe des ordonnées représente une fonction affine . Si une droite ( D) a pour équation de la forme « » , elle représente la fonction affine définie par «» 2°)Proportionnalité des accroissements . Soit « » une application affine définie par Les accroissements algébriques de sont proportionnels aux accroissements de « » . Le coefficient de proportionnalité est « ».
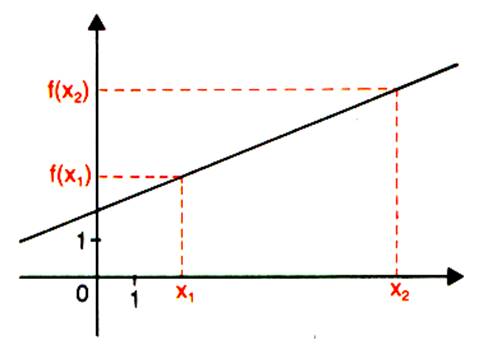
			Interprétation graphique .

	(D) a pour équation : Quand « » augmente de , alors augmente de « ». Quand « » augmente de, alors augmente de « ».
			Si « » augmente de , alors augmente de « ». Si « » augmente de , alors augmente de « ».

	3°) Détermination d’une application affine . ( recherche de « ») Une application affine est déterminée par la donnée de deux nombres distincts et de leurs images. Si et alors le coefficient « a » de f(x) dans f(x) = a x + b est égal à


	FIN DU RESUME.