Juin 2014		Niveau : Classe de collège : 4^ème
Pré requis:		Voir programme de collège 4^ème
Objectifs les égalités : vocabulaire 1EG1
égalités les égalités : vocabulaire 2 EG2
Expression algébrique (niveau 2)

ENVIRONNEMENT du dossier :

INDEX : warmaths

Objectif précédent : 1°) Développer …… 2°) Première approche : niveau V

Objectif suivant : « factoriser » Développer (suite )

· Liste des cours d’algèbre. · Aller vers le corrigé

.

DOSSIER : LES SOMMES ALGEBRIQUES et applications

Fiche 1 : calcul de la moyenne

Fiche 2 : Calcul des coordonnées du milieu d’un segment.

- Sur un droite.

- Dans le plan.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Fiche 1 : Calcul s de moyennes .

1°) Calculs d’une moyenne .

Info +++ @

(soit une moyenne de note par exemple ) · Moyenne de 12 et 18 : ( 12 + 18 ) 2 = … …. = …… · Moyenne de 8 ; 15 ; 4 : ( 8 + 15 + 4 ) 3 = ….. …… = …… · Calculez la moyenne de : 11 ; 8 ; 4 ; 18 ; 7 ; 15 ; 9 ; vous trouvez : ……………( ………. ………= ……..)

Remarque 1 : Il est possible que la division « ne tombe pas juste » . Exemple : faîtes la moyenne de 13 ; 6 ; 18 : ( 13 + 6 + 18 ) 3 = 37 3 ; en faisant la division : on obtient : 12 , 333333333 La division ne se termine pas. Vous obtenez environ : 12 , 33 Dans le cas d’une moyenne de notes , on arrondirait à « 12 » ou « 12,5 »

2°) Moyenne de nombres relatifs.

Moyenne de ; - 3 ; 7 ; - 4 ; 9 ; - 2 ; 5 ; ………………….. ( - 3 + 7 – 4 + 9 – 2 + 5 ) 6 = 12 6 = +2

Remarque 2 : Il se peut que la somme soit un nombre relatif négatif , dans ce cas , pour calculer la moyenne , vous effectuez la division sans vous occuper du signe et vous attribuez le signe « - » au résultat. (cette règle sera justifiée dans la suite de cette fiche ) . Exemple ( - 24 3 = - 6 ) · Moyenne de : 1 ; - 9 ; - 7 ; 3 : …. ( + 1 – 9 – 7 + 3 ) 4 = - 12 4 = - 3 Activité n°1.. Calculez la moyenne de : - 7 ; 5 ; - 4 ; - 8 ; - 6 ; 3 ; - 5 ; 2 ………………….vous trouvez : ……………… = ………………….

3°) Autre façon de calculer une moyenne. Souvent, vous calculez la moyenne de vos notes pour savoir si vous avez plus ou moins de « 10 ». Supposez que vous avez obtenu les notes suivantes ; 5 ; 12 ; 18 ; 15 ; 9 ; 17 ; 8 ; . Par rapport à « 10 » : la note « 5 » vous fait perdre « 5 » points, c'est-à-dire « -5 » Par rapport à « 10 » : la note « 12 » vous fait gagner « 2  points », c'est-à-dire « +2 » Aussi, complétez le tableau donnant l’écart de vos notes par rapport à « 10 ».

Notes

5

12

18

15

9

17

8

………..

Somme

Ecarts

.-5

+2

+8

+5

.-1

+7

.-2

………

←Somme

La somme des gains ou des pertes ( par rapport à « 10 » ) est alors ……  « 14 » …….. Ce gain ( ou cette perte) total est à répartir sur les « 7 » notes. Votre moyenne est alors de : 10 + ( …. 7 ) = 10 +…… = …….. Vérifiez en calculant la moyenne par la première méthode , vous trouvez : ….. 7 = ……

Remarque 3 : Dans la deuxième ligne du tableau, si l’on enlève les traits verticaux, on obtient :

.-5

+2

+8

+5

.-1

+7

.-2

= 14

Nous sommes en présence d’une somme algébrique ( les signes d’addition sont en sous-entendus)

Activité n°2 : On vous demande de calculer la moyenne de  : 5 ; 8  ; 14 ; 16 ; 4 ; 12 ; 7 ; 6 . Ecart de rapport à « 10 » : ……………………… - 5 ; - 2 ; + 4 ; + 6 ; - 6 ; + 2 ; - 3 ; - 4 ; ← soit la somme = - 8 La moyenne est alors de : 10 + ( ….. 8 ) = 10 …….. = …… .. vérifiez par la 1^ère méthode. - Calculez de même la moyenne de 8 ; 13 ; 15 ;7 ; 1 ;9 ;6 11 ; 3 ; 2 ; vous trouvez …………………. : ………

4°) Calcul mental de la moyenne.

Info +++ @ sur le calcul mental..

Exemple :

Variation des écarts

Variation des écarts

Variation des écarts

Variation des écarts

Variation des écarts

Notes

16

8

15

6

13

11

Ecarts

+6

-2

+5

-4

+3

+1

+4

+5

-4

+3

+1

sommes

+4

→

+9

→

+5

→

+8

→

+9

Somme finale = +9

La moyenne est alors «  10 + ( …….. ) = 10 + …… = …….. . Vérifiez par la 1^ère méthode : ……

Activité n° 3….

Calculez mentalement la moyenne de : 8 ; 6 ; 13 ; 15 ; 7 ; 4 ; 5 ; 2 ; 12 ; …………. vous trouvez : ………………………. Et calculez la moyenne de : 12 ; 13 ; 5 ; 7 ; 8 ; 15 ; 6 ; 14 ; 16 ; 9 ;8 : .vous trouvez : …………………………

Fiche 2 : Calcul des coordonnées du milieu d’un segment. - Sur un droite. - Dans le plan.

Info +++@ ..les coordonnées du milieu d’une droite (segment)

I ) Milieu d’un segment sur une droite graduée :

« A » et « B » sont deux points d’une droite graduée. Le point « A » a pour abscisse ( -3) et le point « B » ( + 7). Placez sur la droite ci-contre le point « M » milieu du segment noté : [ AB] Donnez l’abscisse de ce point : M  a pour abscisse : ……………

Vérifiez que cette abscisse est égale à la demi-somme des abscisse de « A » et « B ». ( C'est-à-dire à la demi –somme des abscisses ) soit

Cas général : Etant donné deux points « A » et « B » d’une droite graduée et « M » le milieu de [ AB] , appelons «  » et «  » et «  » les abscisses respectives de « A », « B » et « M » et «  » la distance de « A » à « B »

On écrit : AM = MB =

En désignant par « B » celui des points qui a la plus grande abscisse, on a : Exprimons «  » de deux façons : ou On a alors :  ; c'est-à-dire : ou encore :

A retenir . L’abscisse du milieu d’un segment est égal à la demi-somme des abscisses des extrémités de ce segment .

Activité n°1…

Complétez le tableau suivant :

Abscisse du premier point

12

8

-5

4

-7

…….

Abscisse du second point

4

-5

-7

-3

4

Abscisse du milieu.

…….

…………

…………

……….

3

-5

II ) Calcul des coordonnées du milieu d’un segment .

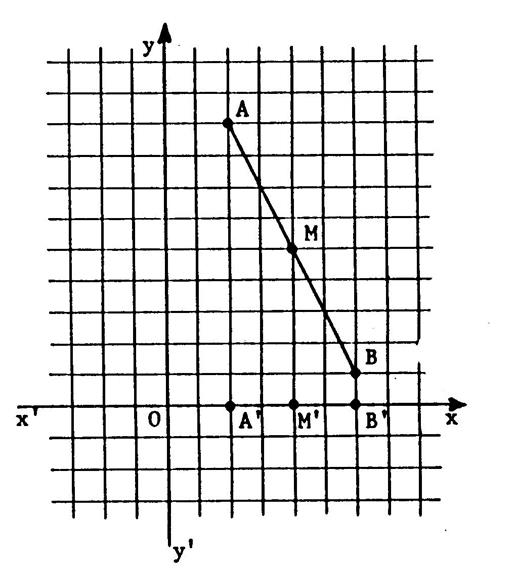
Soient : Deux axes de coordonnées : et y’ y. Ces deux axes sont perpendiculaires et on le même origine « O ». Le point « A » a pour«  coordonnées (+2) , (+ 9) . On écrit A ( 2 ;9). Le point « B » a pour«  coordonnées (+6) , (+ 1) . On écrit A ( 6 ;1). Le point « M » est le milieu de [ AB] . Nous allons déterminer ses coordonnées . Considérons la projection orthogonale sur . - Le point "A" a pour projeté le point « A’ » sur l’axe .. Donc « A » et « A’ » ont la même abscisse : « ….. » - Le point "B" a pour projeté le point « B’ » sur l’axe .. Donc « B » et « B’ » ont la même abscisse : « …. » - Le point "M" a pour projeté le point « M’ » sur l’axe .. Donc « M » et « M’ » ont la même abscisse. D'autre part , puisque « M » est le milieu de [ AB] , son projeté « M’ » est le milieu de [ A’B’]. ( voir propriété 7 vu dans la fiche « 4 » de cette leçon)

Donc l’abscisse de « M’ » est la demi-somme des abscisses de « A’ » et « B’ ». Donc l’abscisse de « M » est la demi-somme des abscisses de « A » et « B ». C'est-à-dire ( abscisse de « M ») = On ferait de même pour les ordonnées, on dira alors : C'est-à-dire ( ordonnée de « M ») =

A retenir : Relativement à un système d’axes de coordonnées , pour tout segment, l’abscisse du milieu est égale à la demi-somme des abscisses des extrémités , l’ordonnée du milieu est égale à la demi-somme des ordonnées des extrémités.

Activités n°2 ..

Complétez le tableau ci-dessous :

Coordonnées des 2 points.

( - 5 ; +2 )

( - 8 ; - 1)

( - 5 ; + 3 )

( + 9 ; - 3)

( + 3 ; + 7 )

( + 8 ; - 3 )

Coordonnées du milieu.

………

……..

( - 6 , - 3 )

( + 5 ; - 5 )

TRAVAUX AUTO FORMATIFS : voir les activités des fiches spécifiques….

CONTROLE:

1° ) Que signifie: Développer ?

2° ) Donner la condition minimum permettant de faire un développement.

3° ) Donner le modèle mathématique représentant ce minimum.

4 ° )Donner le modèle mathématique sur le développement de ( a + b ) ( c + d )

EVALUATION :

I ) Développer les expressions suivantes :
Série 1	résultat
9 ( 3 + 5 ) = (pour cet exercice uniquement ne pas effectuer les calculs!!)
Série 2
Série 3
Série 4
a (a b + c^2f )

II ) Développer les expressions suivantes et réduire et ordonner quand cela est possible : Nota pour « réduire » il faut avoir fait « factoriser »,il vous faudra reprendre ce travail qu’après avoir traité cet objectif !

Série 2	développer	Réduire	Ordonner
( x +1 ) ( x -2 ) =
x +5 ) ( 3x -2 ) =
( -4x +3 ) ( 5 x - 6 ) =

Série 3	développer	Réduire	Ordonner
( x +5 ) ( x + 5 ) =
( x -5 ) ( x - 5 ) =
( x +5 ) ( x - 5 ) =

Série 4	développer	Réduire	Ordonner
( 2x +3 )^2 =	Voir les I.R.
( -3x +1 ) ^2 =	Voir les I.R.

Série 5	développer	Réduire	Ordonner
( a + b )^2 =	Voir les I.R.
( a - b )^2 =	Voir les I.R.
( a + b ) ( a - b ) =	Voir les I.R.

Développer , réduire , ordonner

A = (x +5 ) ( 2 x – 1 ) – 3 (2x – 5 )

INTERDISCIPLINARITE

Géométrie

Calculer l'aire d'une surface	Longueur	largeur
Rectangle	L = x +a	l = x - b