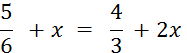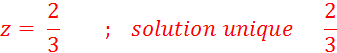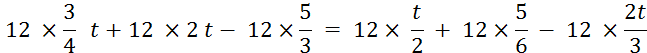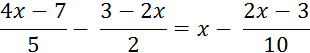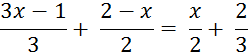Novembre 2014		Niveau : Classe de collège : 4^ème
	CORRIGE.	Retour vers les fiches à travailler.
Pré requis:		Voir programme de collège 4^ème
Objectifs les égalités : vocabulaire 1EG1
égalités les égalités : vocabulaire 2 EG2
Expression algébrique (niveau 2)

ENVIRONNEMENT du dossier :

INDEX : warmaths

Objectif précédent : 1°) Développer …… 2°) Première approche : niveau V

Objectif suivant : « factoriser » Développer (suite )

· Liste des cours d’algèbre. · Aller vers le corrigé

.

DOSSIER : EQUATIONS et RESOLUTION DE PROBLEMES .

Fiche 1 : Approche

Fiche 2 : « Egalité » et « équation. »

Fiche 3 : Propriétés des égalités. 

Fiche 4 : Résolution d’équations.

Fiche 5 : Résolution d’équation ( suite )

Fiche 6 : Résolution de problèmes.

Fiche 7 : Situations problèmes

Fiche 8 : Résolution d’équations ( avec dénominateurs) .

Fiche 9 : Situations problèmes .

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Fiche 1 : Approche

Problème :

Paul dit à Lison : Pense à un nombre, ajoute « 3 » à ce nombre, multiplie par « 5 » ce que tu viens de trouver puis retranche « 7 » au résultat. Dis-moi combien tu trouves, je te dirai le nombre auquel tu as pensé.

Réponse de Lison : « 93 ». Comment Paul fera-t-il pour trouver le nombre ?

Faisons un essai :

Supposons que Lison ait pensé au nombre « 13 ». Ecrivons l'ensemble des calculs à effectuer puis effectuez ces calculs :

………………………………………………..  « 13 » est-il la bonne réponse ?

· Pour résoudre ce genre de problème, on raisonne de la manière suivante : On imagine que l'on a trouvé la solution et que l'on fait la vérification.

Pour cela, on représente le nombre cherché par une lettre.

Appelons-le «  » (par exemple) et faisons comme on a fait pour 13.

93 ..  Ce qui peut s'écrire

Vous êtes en présence d’une « équation » , « » est appelée l’inconnue.

Tout nombre mis à la place de «   » et pour lequel l'égalité correspondante est vraie est appelé solution de l'équation.

« 13 » n'est pas solution de cette équation car il conduit à 73 = 93 qui est____________________________________________________ …….

Résoudre une équation, c'est trouver (toutes) les solutions de cette équation.

· Nous allons résoudre cette équation.

Grâce à la définition de la différence de deux nombres,

dire que c'est dire que

c'est-à-dire

Grâce à la définition du quotient de deux nombres,

dire que c'est dire que c'est-à-dire

et dire que c'est dire que c'est-à-dire _________

Vérification 5 donc «  17 » est solution de l'équation.

Réponse à la question du problème : Le nombre pensé par Virginie est

Fiche 2 : « Egalité » et « équation. »	Info +@+ égalité-équation-propriété+
est une égalité. C'est une phrase mathématique. Elle est vraie. Le verbe de cette phrase est " " qui se lit " égale" ou " est égal à".
A retenir : Une égalité est une phrase mathématique qui se présente sous la forme «   » dans laquelle «  » et « » représente le même objet.
Dans l'équation d'inconnue , figure aussi le signe " ",mais on ne peut pas dire à priori si cette phrase est vraie ou fausse :Tout dépend du nombre mis à la place de l'inconnue . Cette équation devient une égalité quand on remplace l'inconnue par une …………..
Vocabulaire	Info ++@ sur « les égalités »
Dans toute égalité (ou équation), ce qui est écrit : - A gauche du signe « = » s’appelle « membre de gauche » ou « premier membre » de l’égalité. - A droite du signe « = » s’appelle « membre de droite » ou « second membre » de l’égalité. Exemple : Dans l'égalité , le premier membre est « » , le deuxième membre est  «  »

Fiche 3 : Propriétés des égalités.		Info +@+ égalité-équation-propriété+
Egalité et « addition » et « soustraction »
et représentant le même nombre, on peut écrire l'égalité . étant un nombre quelconque, et représentent le même nombre. On peut donc écrire l'égalité et de même
A retenir : En ajoutant ( ou en retranchant )un même nombre aux deux membres d’une égalité , on obtient une nouvelle égalité.
Exemple : désignant un nombre tel que ,- on peut écrire 7________________________________________
TRANSPOSITION DE TERMES. étant des nombres quelconques, par définition de la différence de 2 nombres, dire que c'est dire que . Vous constatez que l'on passe d'une égalité à l'autre en faisant passer «  » d'un membre dans l'autre en changeant le signe qui le précède
	et .
On dit que l'on a transposé « b » (en changeant le signe qui le précède)
· De même, dire que «  » c'est dire que «  »
A retenir : Etant donné une égalité de nombres, on obtient une nouvelle égalité en « transposant un terme» d’un membre dans l’autre ( en changeant le signe qui le précède ).
Activité n°1 : étant des nombres tels que soit une égalité, transposez les termes qu'il faut pour obtenir une égalité dans laquelle les lettres soient dans le membre de gauche et les autres termes dans le membre de droite.
par transformation :
Activité n°2 : Dans le cas de l'égalité , Dites en l'expliquant oralement si vous pouvez appliquer directement la règle précédente. Faites ce qu'il faut pour pouvoir appliquer cette règle et écris une nouvelle égalité dans laquelle les "" soient seuls dans un même membre.
Il faut développer
Egalité et multiplication ou division .
et représentant le même nombre, on peut écrire l'égalité . étant un nombre quelconque, et représentent le même nombre. On peut donc écrire l'égalité . De même, à condition que «  » ne soit pas nul, on peut écrire
A retenir : En multipliant ou en divisant par un nombre non nul les deux membres d’une égalité , on obtient une nouvelle égalité.
Activité n°… : Exemples représentant des nombres, vous allez " simplifier" les égalités suivantes.
peut s'écrire c'est-à-dire
peut s'écrire c'est-à-dire
peut s'écrire __________________________________ c'est-à-dire
peut s'écrire c'est-à-dire
Cas où Contrôle que l'égalité est vraie. Peut-on écrire non D'une manière générale, on a sans avoir forcément

Fiche 4 : Résolution d’équations.	Info ++ @ : résoudre une équation.
On se propose de résoudre l'équation d'inconnue x c'est-à-dire trouver tous les nombres qui, mis à la place de «  » , sont tels que l'égalité correspondante soit vraie. En imaginant que «  » représente une solution (s'il en existe), alors est une égalité. On peut donc lui appliquer la règle de transposition (fiche 3). Transposons « 9 ». On obtient : ______________ c'est-à-dire " " et " " sont des phrases vraies pour les mêmes valeurs de L'équation possède une solution unique : le nombre «  »____________________________________________________ ___ Donc, l'équation possède la solution unique : ____________________________________________________________ «  »
Méthode : Pour résoudre une équation, on remplace l'équation donnée par une équation ayant les mêmes solutions mais qui s'écrit plus simplement. La plus simple étant de la forme ; «  » est un nombre bien déterminé.
Règle : Etant donné une équation, on obtient une équation ayant les mêmes solutions en transposant un terme d’un membre dans l’autre ( en changeant son signe ) ..
Exemple 2 : Résolvons l'équation d'inconnue . Transposons « » et «  » , on obtient : Ce qui s'écrit__________ Donc l'équation possède la solution unique : «  »
Exemple 3 : vous devez résoudre l'équation d'inconnue « » de deux façons différentes.
1^ère façon : Transposons «  » , on obtient : Ce qui s'écrit «  » est l'opposé de « » donc «  » peut s'écrire «  » . Donc l’équation possède la solution unique : «  »
2^ème façon : Transposons «  » et «  » , on obtient : « » Ce qui s’écrit «   » c'est-à-dire «   » On retrouve bien la même solution que précédemment.
Exemple 4 Résolvez l’équation d’ inconnue « y ». En transposant , on obtient Et après simplification , on obtient «  = » Donc l’équation possède la solution unique :
Activités : Résolvez les équations suivantes d’inconnues respectives «   »
	; ;

Fiche 5 : Résolution d’équation ( suite )
Exemple 1 On se propose de résoudre l'équation d'inconnue «  ». En imaginant que x représente une solution (s'il en existe), alors est une égalité. On peut donc lui appliquer la règle du « fiche 3 ». En divisant les deux membres par « 3 » , on obtient Les équations «  3x = 36 » et « x = 12 » ont les mêmes solutions. Donc, l'équation 3x = 36 possède la solution unique « 12 »
Exemple 2 Résolvez l'équation d'inconnue «  ». En raisonnant comme précédemment mais en multipliant les deux membres par «  », on obtient : ce qui s'écrit Les équations et ont les mêmes solutions. Donc, l'équation possède la solution unique : «  »
A retenir : Etant donné une équation , on obtient une équation ayant les mêmes solutions en multipliant ou en divisant par un même nombre non nul les deux membres de cette équation.
Exemple 3 Résolvez l'équation d'inconnue . En divisant les deux membres par «  » , on obtient : L'équation possède donc la solution unique :
Exemple 4 Résous l'équation 2t - 5 - 13 - t d'inconnue t. En transposant__ et____ , on obtient : 2t__
Exemple 5 Résolvez l'équation d'inconnue . On ne change pas les solutions de l'équation si l'on transforme l'écriture de chacun des deux membres de l'équation. En particulier, on peut développer : On obtient : en transposant les termes convenables, on obtient qui s'écrit - 8x = - 28 En divisant les deux membres par_____________ on obtient :__________ ____ L'équation donnée possède donc la solution unique : _______________________
Activités : Résolvez les équations suivantes ( à faire sur une feuille à part)
	;  ;
	;

Fiche 6 : Résolution de problèmes.	Info +@ +++ sur la résolution de pb.
Problème 1 Trois personnes se partagent une somme d'argent de 1630 € . La deuxième a 90 € de plus que la première et la troisième a 50 € de moins que la première. Trouve la part de chacune.
Pour résoudre un tel problème, on raisonne de la manière suivante : On imagine que l'on a trouvé la solution et que l'on fait la vérification. Supposons que l'on ait trouvé la part de la première personne. Appelons-la «  » La part de la deuxième personne est alors (en € ) 90______________________ La part de la troisième personne est alors (en €) – 50 ________________________ ~~ La somme totale (en € ) est alors : II ne te reste plus qu'à résoudre cette équation.
:  ; :  ;  ; Les parts sont alors : la première : 530 € ; la deuxième : 620 € , la troisième : 480 €
Méthode de résolution La résolution du problème précédent comporte quatre étapes. Il en est de même pour tous les problèmes de ce genre. 1°) Choix de l'inconnue et désignation de cette inconnue (ou des inconnues). Dans le problème précédent, l'inconnue est la part de la première personne. Cette inconnue a été désignée par x_ 2°) Mise en équation(s) C'est la traduction de l'énoncé en langage mathématique. On procède comme si, connaissant la solution, on faisait la vérification. 3°) Résolution de l'équation Comme tu l'as appris aux paragraphes précédents. 4°) Réponse à la question du problème La solution que l'on vient de trouver en langage mathématique doit être traduite en langage courant et interprétée.
Problème 2 : Pierre et Clotilde décident de constituer chacun une cagnotte. Pierre a mis 15€ dans la sienne et Clotilde a mis 43 € . Ils décident alors de mettre chaque jour 1 € dans leur cagnotte respective. Dans combien de jours la cagnotte de Marc sera-t-elle le double de celle de David ? 1°) Choix de l'inconnue. Appelons « » le nombre de jours cherché. 2°) Mise en équation Au bout de « » jours, dans la cagnotte de Pierre , il y a (en € ) : dans la cagnotte de Clotilde , il y a (en € ) " La cagnotte de Clotilde est le double de celle de Pierre " se traduit en langage mathématique par (en € ): 3°) Résolution de l'équation ; ; 4°) Réponse à la question du problème : Dans jours la cagnotte de Marc sera le double de celle de David. Remarque : Si la résolution de l'équation avait donné un nombre non entier, le problème posé n'aurait pas eu de solution
Fiche 7 : Situations problèmes	Info plus @@@ et d’autres problèmes encore..
Faites la rédaction de ces problèmes sur une feuille à part. vous n'indiquerez ici que la réponse à la question du problème.
Problème 1 Un père et un fils ont leur anniversaire le mime jour. Le père a 46 ans, le fils 12 ans. Dans combien d'années l'âge du père sera-t-il le triple de l'âge du fils?
Problème 2 : Simon et Victor jouent aux billes. Avant la partie, Simon avait 26 billes, Victor en avait 14. Simon a perdu et Victor possède maintenant trois fois plus de billes que Simon . Combien Victor a-t-il perdu de billes ?
Problème 3 On doit partager équitablement une somme d'argent entre plusieurs personnes. Si on donne 200 € à chaque personne, il reste 400 €. Si on donne 250 € à chaque personne, il manque 750 €. Quel est le nombre de personnes ? Quelle est la somme à partager ?
Problème 4 Dans une classe, il y a deux fois plus de filles que de garçons. 1°) Un jour où 4 filles et 4 garçons sont absents, il y a trois fois plus de filles "* que de garçons. Combien y a-t-il de filles et de garçons dans cette classe ? Indication Prenez comme inconnue le nombre de garçons. 2°) Dans la même classe, combien faudrait-il qu'il y ait de filles absentes et de garçons absents (le même nombre pour les deux) pour que le nombre des filles soit le quadruple du nombre des garçons ? Indication Appelez « » le nombre de filles absentes, (c'est aussi le nombre de garçons absents).
Problême 5 Un cycliste va d'une ville A vers une ville B à la vitesse de 30 km/h. Une heure plus tard, roulant à la vitesse de 90 km/h un automobiliste va de A vers B Combien de temps après son départ rencontrera-t-il le cycliste ? Indication Pour la mise en équation, exprime le fait qu'au moment de la rencontre, le cycliste et l'automobiliste ont parcouru la même distance.
Problème 6 Le salaire journalier d'un couple est 600€ (quand ils travaillent tous les En un mois, le mari a travaillé 21 jours et la femme 18 jours. Leur salaire mensuel total a été 11 790 €. Quel est le salaire journalier de chacun d'eux ?
Problème 7 A l'arrivée d'une course, pour récompenser les quatre premiers, on décide de partager 2150 € de la manière suivante : On donne une certaine somme au 4°. Au 3°, on donne le double de ce que l'on a donné au 4° plus 25 €. Au 2°, on donne le double de ce que l'on a donné au 3° plus 25 € Au 1°, on donne le double de ce que l'on a donné au 2° plus 25 €. Déterminez la part de chacun d'eux.

Fiche 8 : Résolution d’équations ( avec dénominateurs)			Info @++++
Vous allez résoudre des équations en utilisant les règles dans les fiches : ………. Et …………..
Activité 1 : Résolvez l’équation : d’inconnue « » . En transposant , on obtient , or L’équation possède la solution unique :
Activité 2 : Résolvez l’équation : d’inconnue « » . En divisant les deux membres par , on obtient , or L’équation possède la solution unique :
Activité 3 : Résolvez l’équation : d’inconnue «» . En transposant , on obtient , or On alors : en divisant les deux membres par , on obtient C'est-à-dire : L’équation possède la solution unique :
Autre méthode : Si on multiplie les deux membres de l’équation par un multiple des dénominateurs, on obtient une équation dans laquelle il n’y a plus de dénominateurs. Pour que le calcul soit le plus simple possible , il est préférable de choisir un multiple commun le plus petit possible . vous choisissez « 6 ».
On obtient alors : On obtient alors : et d’autre part On obtient alors l’équation : A vous de finir de résoudre cette équation : ; ; ;
Activité 4 : Résolvez l’équation :  ; d’inconnue «  » Le multiple commun des dénominateurs le plus petit possible est « 12 » Multiplions les deux membres de l’équation par ce nombre et développons , on obtient : Après simplification on obtient : En transposant les termes qu’il faut , on obtient : ; ; et en divisant les deux membres par : « 5 » on obtient  ; L’équation proposée possède la solution unique :
Activité 5 : Résolvez l’équation : d’inconnue « ». Le multiple commun des dénominateurs le plus petit possible est : « 18 » Et après simplification : Attention : il ne faut pas oublier de mettre les parenthèses dès que l’on enlève le trait de fraction. En développant, on obtient : finissez la résolution. ;
Activité 6 Résolvez l’équation : d’inconnue «  » .
Vous avez pu constater que dans la résolution des équations précédentes , on est toujours passé par une équation de la forme «   » dans laquelle «  » est l’inconnue et «  » et «  » des nombres connus. Pour résoudre l’équation de la forme «  » , on divise les deux membres de l’équation par « », à la condition que « » ne soit pas nul . On obtient alors «  » l’équation possède la solution unique «  ». · Que se passe –t-il si «  » ? C’est ce que nous allons étudier maintenant.
Activité 7 : Résolvez l’équation d’inconnue «  ». En développant, on obtient et en transposant : ; c'est-à-dire : Quel que soit le nombre mis à la place de « y » , Donc ne peut –être égal à « -3 ». Donc l’équation n’a pas de solution.
Activité 8
Résolvez l’équation d’inconnue «  » En multipliant les deux membres par « 6 » et en simplifiant , on obtient : et en développant , on obtient : En transposant : ; c'est-à-dire Quel que soit le nombre mis à la place de « z » , est toujours vraie. Donc , tous les nombres sont solution de l’équation. On énoncera alors :
Théorème :
	Etant donné l’équation «   » d’inconnue «  », Si «  » l’équation possède la solution unique : Si «  a = 0 » .
Activité 9 : Résolvez les équations suivantes : ( à faire sur une feuille à part )
Fiche 9 : Situations problèmes .
Activité 1 : Le périmètre d’un champ rectangulaire est de « 416 m » . La largeur est les de la longueur. Calculez la longueur et la largeur de ce champ.
Activité 2 : Une somme d’argent est partagée entre trois personnes. La première reçoit de la somme plus « 57 € ». La deuxième reçoit de la part de la première plus « 74 € » . La troisième reçoit « 106 € ». Quelle était la somme totale.
Activité 3 : On coupe un ruban de la manière suivante : On en enlève puis on enlève du reste , puis on enlève du nouveau reste. Le ruban ne mesure plus que « 1,8 m », quelle était la longueur initiale du ruban ?.
Activité 4 : Un marcheur effectue une randonnée de «  4 h » . Le parcours comporte le tiers de montée, la moitié de descente et le reste à plat. Sa vitesse En montée est de « 4 km/h » , en descente « 6 km /h » , sur le plat « 5 km/h » . Quelle est la longueur du parcours.
Indication : En choisissant comme inconnue la longueur du parcours, évaluez le temps passé dans chacun des 3 cas. : montée , descente , plat. N’oubliez pas que le temps est égal à l’espace parcouru divisé par la vitesse.

TRAVAUX AUTO FORMATIFS : voir les activités des fiches spécifiques….

CONTROLE:

EVALUATION :