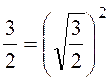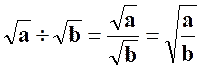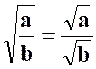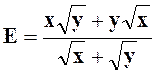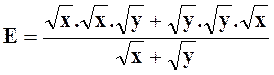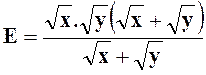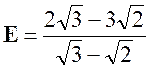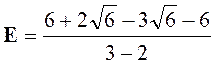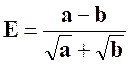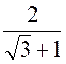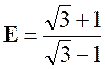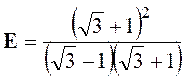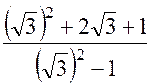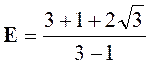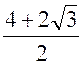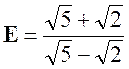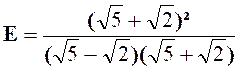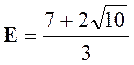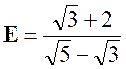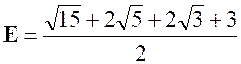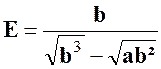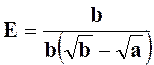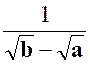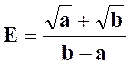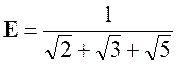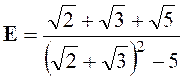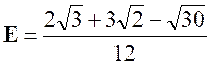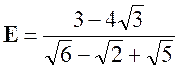COURS

1°)  Racine carré arithmétique.

Etant donné un nombre positif « a » sa racine carrée est le nombre « x » tel que :

·       «  x ² = a »        ( 1)

on écrit  

·       «   x =  »         ( 2 )

« x » est un nombre positif.

On dit que les formes  ( 1 ) et ( 2 ) sont équivalentes . C’est pour cela que nous écrivons que : «  tout nombre positif est le carré de sa racine carrée »

11  = 

17  = 

Ce qui nous permet de transformer : «  x² - 13 »     en      ( x + )  ( x - )

Le symbole  «   »  s’appelle « un radical ».

2°)  Propriétés :

Elles sont contenues dans les égalités :

 ( 1 )

( 2 )

Etant bien entendu que « a » et « b »  sont positifs séparément.

Ces propriétés permettent souvent d’ alléger l’écriture d’un nombre soumis à une extraction de racine carrée :

Exemples :

  =     = 3            ;  et   ;     =    = 

On doit toujours penser à ces transformation. Par exemple, dans un calcul, il ne faut pas traîner avec soi «  »  . il faut écrire : «  »

Exercices types :

Exercice 1 –   Calculer :  

Solution : On développe en utilisant ( a + b)² et la propriété distributive.

on applique la définition et la propriété (1) :

on réduit et on obtient : 

Exercice 2 –   Calculer :

Indications :

Réponse :                    

Exercice 3 –   Calculer :

Réponse :

La simplification des fractions, quand elle est possible, s’opère en décomposant, comme de coutume, le numérateur et le dénominateur en produits de facteurs

Info @

Exercice 4 –   simplifier :

                                  avec «  x ; y > 0 »

Solution : remarquer que    et de même pour « y » :   dés lors :

    =     on simplifie ; il reste

Exercice 5 –   simplifier :

Indications= multiplions les deux termes par :

Réponse :

Exercice 6 –   simplifier :

                      avec  « a > 0 et b > 0 »

Réponse :

Info @

4°) Quantité conjuguée.

Cours : Etant donné l’expression : «  »  , la quantité conjuguée est : «  »

De même :

conjuguée

conjuguée

conjuguée

Principe :On ne doit  jamais laisser subsister au dénominateur d’une fraction une expression binôme  ( ou trinôme)contenant un radical.

Par exemple : On ne garde pas 

A cause de l’identité des différences de deux carrés, le produit d’une quantité par sa conjuguée est rationnel ( ne contient plus de radical : )

Le procédé consiste donc à multiplier les deux termes de la fraction par la quantité conjuguée du dénominateur. ( voir l’exercice ci-dessus  N° 5)

Exercice 7 –  Transformer :

Solution :

On multiplie les deux termes par «  »

   =  

   =    = 

Exercice 8 –  Transformer :

Indications : 

Réponse : 

Exercice 9 –  Transformer :

Réponse : 

Exercice 10 –  Transformer :

    avec    «  a > 0 »    et     « b > 0 »

Solution : remarquer d’abord que :

    et 

dés lors :    = 

intervention de la quantité conjuguée du dénominateur :

Exercice 11 –  Transformer :

Indication : faire intervenir

Réponse : 

Exercice 12 –  Transformer :

Réponse :