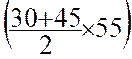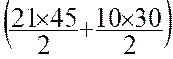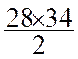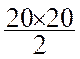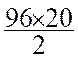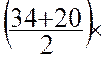Pré requis:

Aire des surfaces curvilignes. ( lecture)

Voir le découpage d’un triangle quelconque en deux triangles rectangles

Quadrilatère convexe et non - convexe

Les polygones

Formulaire ( calcul des aires des figures élémentaires)

ENVIRONNEMENT du dossier:

Index		AVANT : Les polygones réguliers Les calculs d’aires de surfaces de bases…	COURS	APRES : Liste des objectifs de calculs d’aire 2°)Aire de surfaces curvilignes. 3°) Devoir	Complément d’Info Les Polygones (7)
	TITRE : Calculs d’ AIRE D’UN POLYGONE quelconque (dit aussi : irrégulier)
	- Définition : Aire d’un polygone quelconque :
	- 1 Type de calcul par décomposition  (addition de surfaces élémentaires) :
	- Par différence :
	- Calculs de l’aire Exercice traité:

Travaux ;			devoirs	Corrigé
TEST	Contrôle	évaluation	Travaux niveau VI et niveau V Dos 200	Contrôle	évaluation
				Travail à donner aux élèves. personnel : préparation du devoir formatif.

Interdisciplinarités : Situations problèmes (matière concernée)

COURS

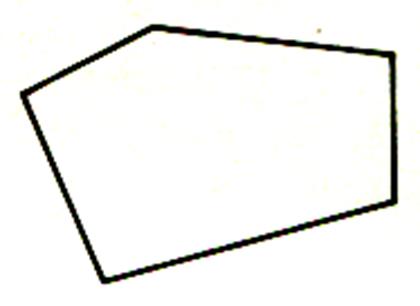
Aire d’un polygone quelconque :

Pour calculer l’aire d’un polygone on divise ces polygones en carrés , rectangles , trapèzes , triangles rectangles ; puis on additionne les surfaces partielles obtenues et on a la surface totale .

On peut aussi entourer le polygone irrégulier par un rectangle circonscrit passant par tous ses sommets ; on calcule la surface des diverses figures , triangles rectangles , trapèzes qui se trouvent en dehors du polygone et on soustrait leur somme de la surface du rectangle circonscrit .

AINSI :

L’aire d’un polygone peut être obtenue soit par décomposition en surfaces élémentaires ( somme = addition des aires) ou par différence ( aire d’un rectangle diminué de la somme des aires exclues)

Principe utilisé pour la décomposition d’un polygone irrégulier en arpentage :

Tracer une droite , si possible la plus longue dans le polygone  ,que l’on appelle « base »; et abaisser sur la base des droites perpendiculaires issues des extrémités des segments (angles) , de sorte à n’obtenir que des carrés ; rectangle ; trapèze ,triangles rectangles .

1 Type de calcul par décomposition :

Exemple 1

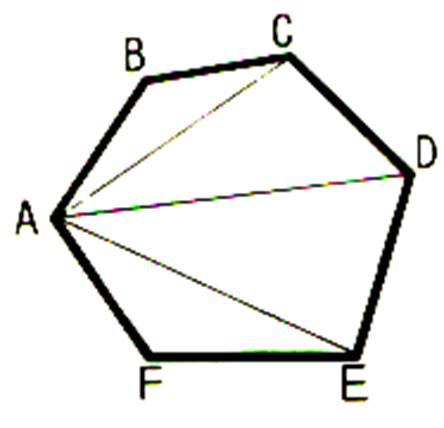
L’aire du polygone ABCDEF est la somme des aires des triangles ABC , ACD , ADE et AEF .

Exemple 2

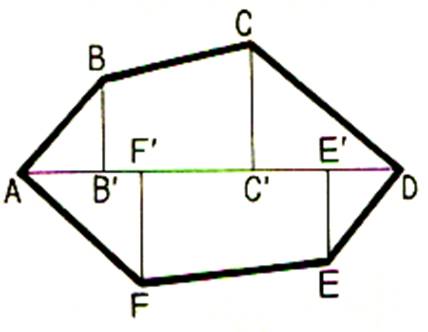
L’aire du polygone ABCDEF est la somme des aires des triangles rectangles ABB’ , CC’D , EE’D , AFF’ et des trapèzes rectangles BCC’B’ et EFF’E’ .

Ce procédé est celui utilisé par les arpenteurs.

Exemple :

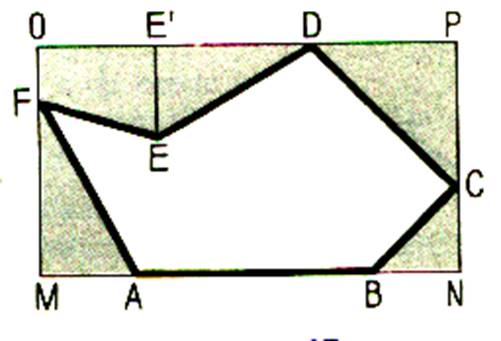
L’aire du polygone ABCDEF est égale à l’aire du rectangle circonscrit OPNM diminuée de la somme des aires des triangles rectangles BNC , CPD , DEE’ et FMA et du trapèze rectangle EE’OF.

Ce procédé est souvent utiliser pour connaître l’aire d’une pièce d’eau .

Calculs de l’aire Exercice traité:

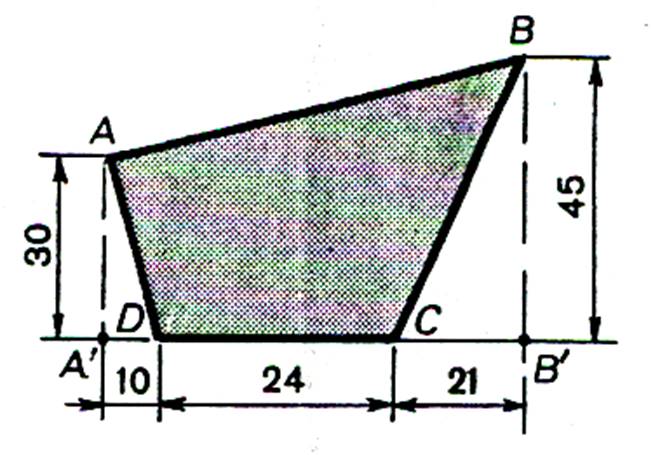
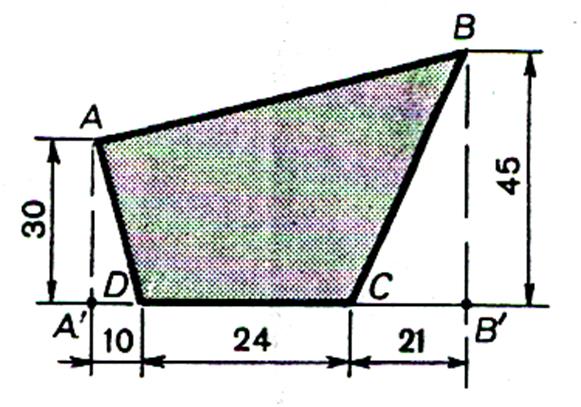
Calculer l’aire de la surface ( ABCD) ; les côtes sont en cm

Aire ( ABCD) = Aire ( AA’BB’) – [Aire ( BB’C) + Aire ( AA’D)]

Aire ( ABCD) = -

Aire = 1440 cm²

Autre problème résolu

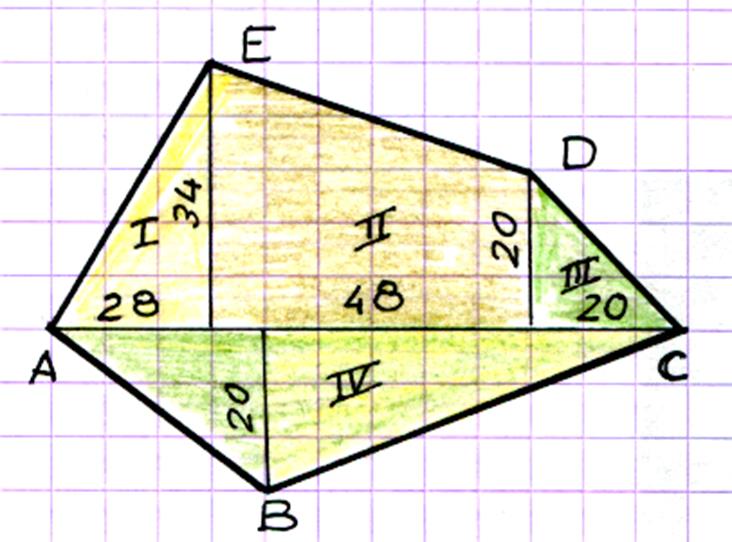
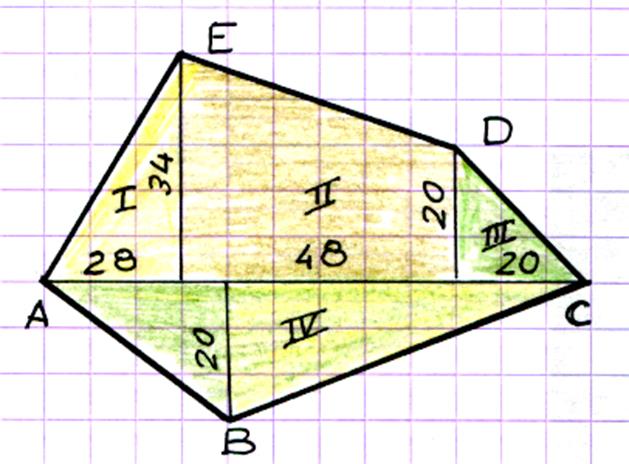
Les relevées d’un plan on données les dimensions suivantes :

Quelle est l’aire de ce polygone ?

Solution : On a tracé la ligne de base AC ;. Sur cette ligne on mène les perpendiculaires des angles B ; E ; D  , et on cherche successivement la surface des triangles I ; III ; IV et celle du trapèze II ;puis on additionne les résultats :

Triangle I : = 476 m²

Triangle II = = 200 m²

Triangle IV = = 960 m²

Trapèze IV =48 = 1296 m²

La superficie totale est de : 2932 m²

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°) A quoi est égale l’aire d’un polygone régulier ?

2°) Citer le nom des deux possibilités pour obtenir l’aire d’un polygone quelconque.

EVALUATION:

1°) Faire le découpage suivant deux cas :

PROBLEMES :

1°) Calculer l’aire de la surface ( ABCD) ; les côtes sont en cm

2°) Les relevées d’un plan on données les dimensions suivantes :

Quelle est l’aire de ce polygone ?

3°) Quelle est l’aire d’un champ qui a la forme d’un quadrilatère irrégulier ADCB .

Vous menez un diagonale AC et sur cette diagonale vous abaissez des perpendiculaires des sommets B et D . Quelle est la superficie du champ si la diagonale mesure 52 m et les perpendiculaires ED et FB mesurent respectivement 23 et 30 m

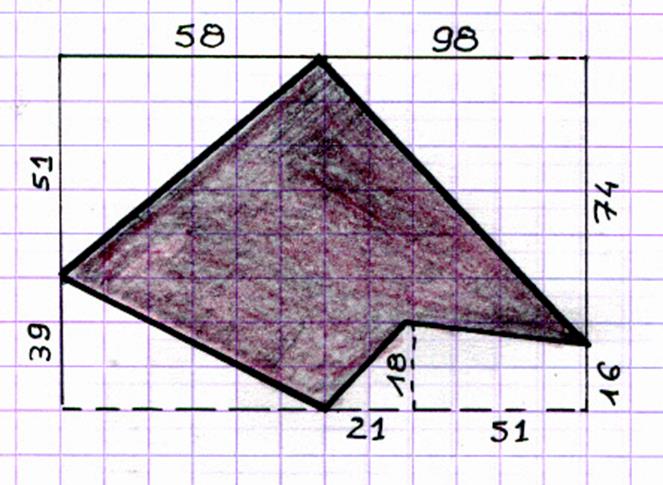
4°) Calculer d’après le plan et les données ci – jointes la superficie représentée par le polygone couvert en gris et circonscrit par un rectangle d’après les mesures indiquées sur le même plan .

5°) Un terrain la forme d’un pentagone irrégulier ABCDE . Pour le mesure vous tracer une diagonale BD , puis sur cette diagonale vous abaissez des perpendiculaires des sommets C, A, E .

Quelle est la superficie d u terrain si la diagonale mesure 46 m et les perpendiculaire CF 16 m , et AG et EH respectivement 21 m et 19 m ?

Quelle est la valeur du terrain à raison de 25 € le mètre carré