1°)  Le quadrillage

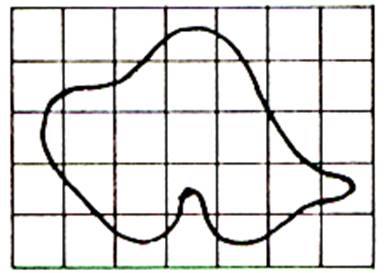
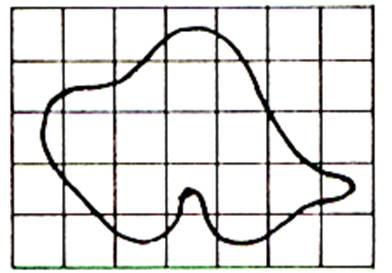
2°) La ligne courbe

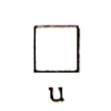
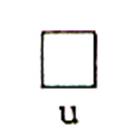
3° )  L’Unité d’aire

Index

AVANT :

Notion « aire »

COURS

APRES :

Liste des objectifs de calculs d’aire

TITRE : AIRE D’UNE SURFACE à frontière curviligne quelconque

I ) Détermination de l’aire par méthode d’approximation graphique 

II ) Encadrement de la mesure de l’aire

III ) Influence de l’unités sur la précision de l’encadrement .

Travaux ; devoirs

Corrigé

TEST

Contrôle

évaluation

Travaux niveau VI et V

Dos :  200

Contrôle

évaluation

COURS

I ) Détermination de l’aire par méthode d’approximation graphique :

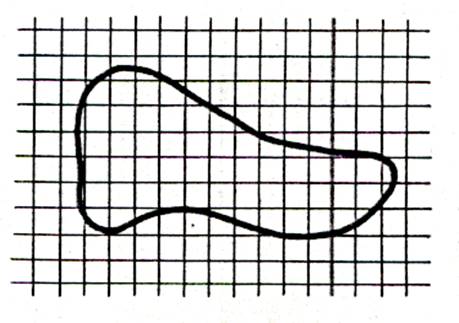
Cherchons à déterminer l’aire de la surface ci- dessous  :

Matériel : du papier  quadrillé  millimétré transparent .

Exemple 

d’application:       Les carreaux ont 1mm de coté

Etape 1 :   Appliquer sur le dessin le papier millimétré ;

Etape 2

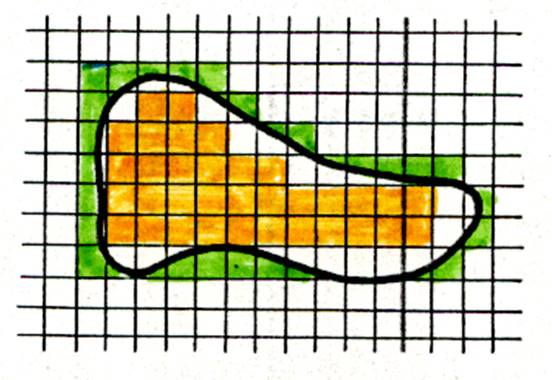
Compter le nombres de petits carreaux « n »  de 1 mm² entièrement à l’intérieurs à la frontière .( 34 carreaux jaunes ).

Compter ensuite le nombre « m » de petits carrés coupés en deux parties par la frontière .( 28 carreaux blancs) .

Pratiquement on peut considérer que , dans l’ensemble , la moitié de ces petits carreaux est intérieur à la courbe .

ce qui peut correspondre à environ 14 carreaux « jaunes »

Etape 3 :

Estimation : l’aire de la surface curviligne est d’environ 48 mm²

C’est une estimation ! ! ! !

On peut en tirer  une formule : Aire = n + (m /2 )   aire exprimée en mm²

Remarque : la détermination de l’aire est d’autant plus précise que le tracé de la courbe est plus fin.

NOTA :  D’autres méthodes de calcul permettant d’évaluer les aires limitées par une courbe . Il existe aussi des appareils  ( planimètres ; intégrateurs ; …) qui en parcourant le contour de la surface , donne mécaniquement la mesure de cette surface .

II) Encadrement de la mesure de l’aire.

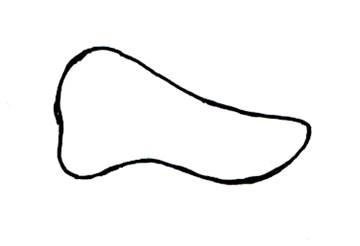
1°)  La figure représente une surface limitée par une courbe quelconque.

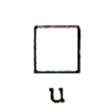
Il n’est pas possible de recouvrir exactement cette surface par des carreaux d’unité « u » :

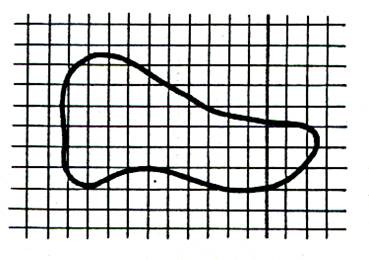
2°) On reprend la  même figure.

On peut la recouvrir partiellement par des carreaux situés à l’intérieur de la courbe .

On compte ainsi  7 carreaux « u »

3°) On reprend la  même figure.

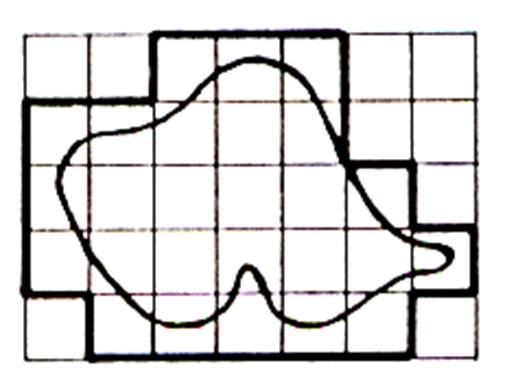
On peut la recouvrir  totalement par des carreaux  mais en débordant .

Le nombre minimum de carreaux  nécessaire à ce recouvrement est de  26 .

On obtient le   croquis :

En conclusion :

Si nous appelons « A » la mesure de l’aire de cette surface ( avec une unité « u ») ces deux recouvrements nous permettent de donner un encadrement de « A »

7u     <    A    <      26 u

Conclusion : la mesure d’une surface limitée par une ligne courbe doit être donnée avec un encadrement  .

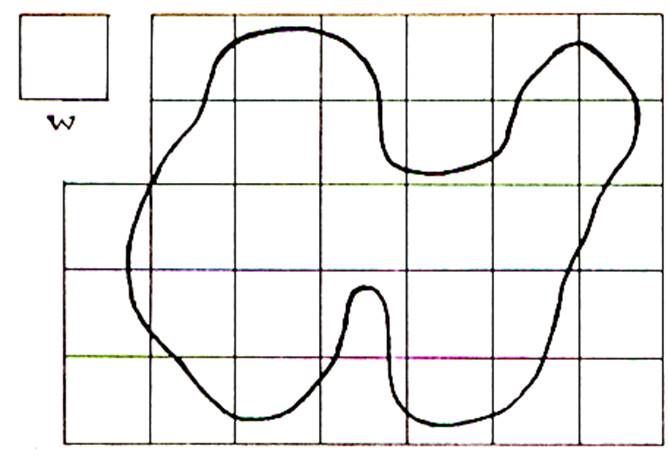
III) Influence de l’unités sur la précision de l’encadrement .

Nous représentons une même surface  dans deux situations de choix d’unité.

Dans les deux cas nous allons mesurer le recouvrement intérieur et extérieur.

Cas  1

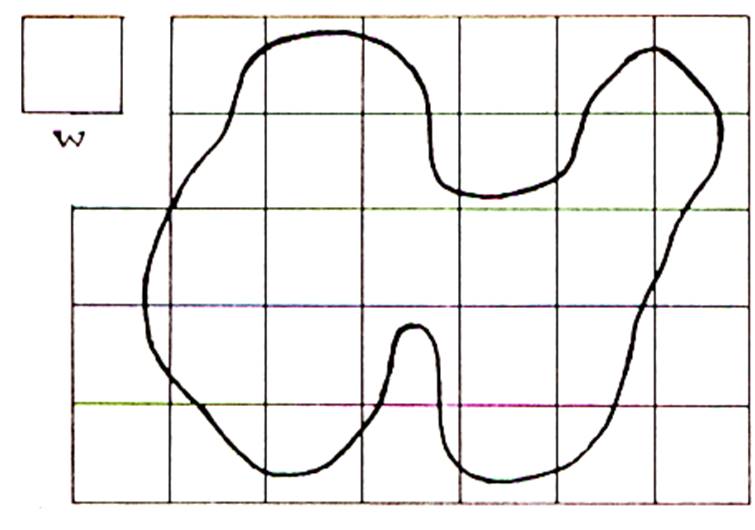
Considérons la surface « S » avec l’unité « w »

a)    on compte  7 carreaux  situés à l’intérieur.

b)    on compte   30 carreaux pour recouvrir totalement « S »

 Nous obtenons l’encadrement de « S » suivant :

7w   <    S    <    30 w

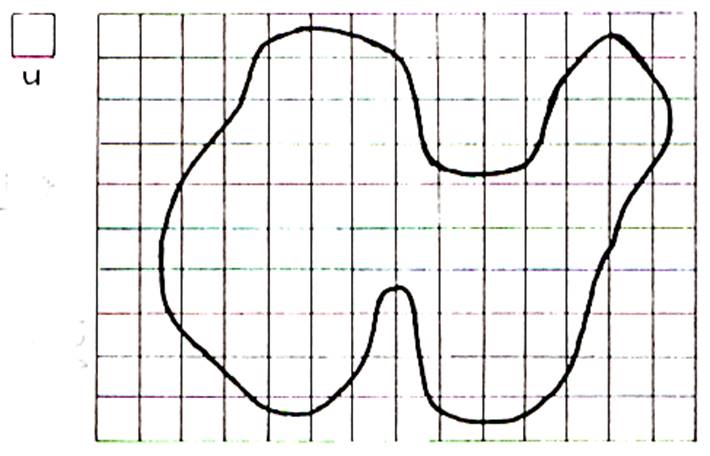
Cas 2 :

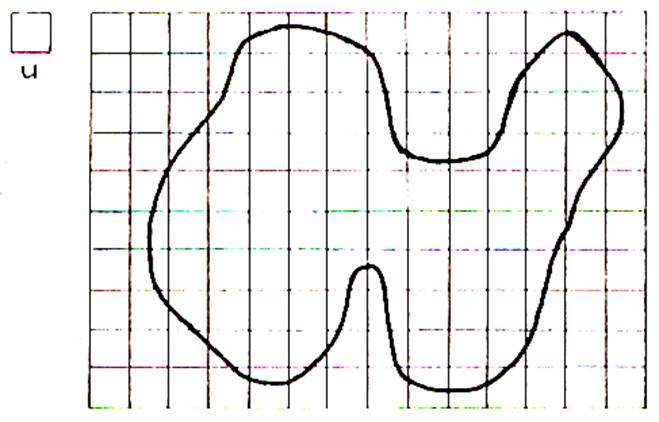
Considérons la surface « S » avec l’unité « u »

a)    on compte  48 carreaux  situés à l’intérieur.

b)    on compte   104  carreaux pour recouvrir totalement « S »

c)     Nous obtenons l’encadrement de « S » suivant :

48  u   <    S    <    104  u

Analyse :   

    sachant que  l’unité  w = 4  unité « u » 

à partir du dernier encadrement de « S » avec « u »:    

              48  u   <    S    <    104  u

on peut donner un autre encadrement de  « S » avec l’unité « w » :

  ( on doit calculer        48 u : 4  =  12 w ;     104 u : 4 =  26 w )

 (1) Soit :               12 w     <    S     <     26 w     ; ( 26 w – 12 w = 14 w )

Si l’on compare cet encadrement « calculé » ci dessus  et l’encadrement

  (2)                     7w   <    S    <    30 w   ; ( 30 w – 7 w = 23 w )

pour (1)  On constate un écart de  14 w  et pour  (2) un écart de  23w ;

 constat :      l’écart  14 w   représente  un plus petit écart  entre la mesure mini et la mesure maxi .l’erreur est moindre .

conclusion :  plus l’unité mesure  choisie est petite ; plus la précision dans la mesure sera proche de la valeur exacte .  

A retenir :

Les unités  d’aire  sont définies à partir des unités de longueur :

Ainsi l’ unité  « mètre carré » est l’aire d’un carré dont la longueur d’un côté est 1 mètre

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Qu’appelle –t-on méthode d’approximation graphique ?

 EVALUATION:  ( pour le corrigé voir le cours)

Par la méthode d’approximation graphique ,  trouver l’aire de la surface suivante

(1 carreau = 1 cm)

( estimée au cm²   près )

III) Influence de l’unités sur la précision de l’encadrement .

Nous représentons une même surface  dans deux situations de choix d’unité.

Dans les deux cas ,mesurer le recouvrement intérieur et extérieur.

Montrer que le cas 2 est plus précis que le cas 1

Cas  1

Cas 2 :