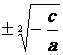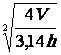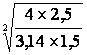|
Racine carré d’un quotient |
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : Voir : les IR
et l’équation produit ax² = 0 . |
DOSSIER :
Résoudre L’ EQUATION
incomplète du second degré : a x² + c = 0
|
TEST |
COURS |
Interdisciplinarité |
|
Dans l’équation du second degré « b = 0 » ; nous obtenons l’équation dite
« incomplète » .
|
|
L’équation s’écrit : « ax² + c = 0 » Elle est équivalente à « a x²
= - c » « x²
= - |
|
|
|
Donc :
1°)
si - 2° )
si - 3°)
si - |
|
|
|
|
|
Exemple : Soit
l' équation : 5 x2- 75 = 0
Résoudre :
|
|
|
|
Soit
: 5 x2-75 = 0 |
|
|
5 x2
= +75 |
|
|
x2 = |
|
|
x2 = 25 |
|
|
|
|
|
"x"
= (+ 5) ou
(-5) |
|
|
Nous
avons donc deux solutions: x ' = (+5 ) x '' = (-
5 ) |
En effet :
(+ 5) 2 = (+25)
(- 5 ) 2 = (+25) |
Représentation graphique :
La représentation graphique de l’équation y = 5
x2- 75 est une parabole ; l’axe « y »
étant l’axe de symétrie , le minimum étant « 75 »
Remarque : :
Pratiquement , pour résoudre une équation du second degré incomplète , il ne
faut pas utiliser ces résultats littéraux , mais refaire le calcul pour chaque équation
considérée.
CONTROLE :
EVALUATION
Résoudre l’équation : 5 x2 - 75 = 0
AIRE d' un CARRE:
|
A = c 2 |
A = aire |
c = longueur d' un coté |
Problème
1:
Calculer le coté d'un carré de 225 centimètres
carrés d' aire:
|
225 cm2 = c 2 |
D'ou c = |
C = + ou -
25 cm Conclusion : le coté du carré vaut 25 cm La
solution négative ne peut convenir. |
Problème
2
Calculer le rayon d'un disque dont on connaît son
aire:
|
A = 200,96 cm2 |
A = 3,14 R2 |
|
Donc 200,
96 = 3,14 r2 |
Après transformation R2 = 64 |
|
R = |
R
= 8 cm |
Problème
3
Quel diamètre convient-il de donner à un cylindre de 1,50 m de haut
pour obtenir une capacité de 25 hectolitres ?
|
25 hectolitres |
25 00 litres |
25 00 décimètres cubes |
2 , 500 m3 |
|
Le volume d'un cylindre: V = |
|
|
4V = 3,14 D2h |
D2 = |
|
|
D = |
|
|
D = 1,456 m |
|
|
|
Le
mouvement uniformément varié
|
V
= vo + a t |
"V " est la vitesse au temps
"t" "V o " est la vitesse
initiale "e"
désigne l' espace parcouru "a" désigne l' accélération du mouvement "t"
temps mis |
|
e = vot + |
"V o " est la vitesse
initiale "e"
désigne l' espace parcouru "a" désigne l' accélération du mouvement "t"
temps mis |
|
Si
le corps part du repos : vo = 0
; alors les formules
deviennent: V =
vo + a t devient V = 0 + a t ; e = vot + |
V = a t e
= + |
|
|
|
Problème
1:
Au départ d'une gare un train met 40 secondes pour atteindre
sa vitesse uniforme de 72 kilomètres à l'heure. Pour s'arrêter , il ralentit sa
vitesse de 0 ,40 m/s-1
On demande :
L' accélération du mouvement de départ.
L'espace parcouru quand il atteint sa vitesse
normale;
Le temps mis pour s'arrêter;
La distance de la gare d'arrivée à laquelle le
mécanicien doit cesser l'admission de vapeur.
1° v = at , d'où a![]()
v = 72
kilomètres à l'heure ou 72 000 mètres en 3600 secondes
ou ![]() = 20 mètres à
la seconde
= 20 mètres à
la seconde
a = ![]() = 0,50m par
seconde
= 0,50m par
seconde
2° e = +![]() a t2 ; e = +
a t2 ; e = +![]() 0,50
0,50 ![]() 402 = 400 mètres.
402 = 400 mètres.
3°) V = vo
+ a t de cette formule nous
tirons :
t = ![]()
mais v =
0 correspond à l' arrêt ; vo = vitesse initiale 72 kilomètres à l'heure ou
20 mètres à la seconde ; a = - 0,40 m accélération "retardatrice".
t = ![]() ; t =
; t = ![]() ; t = 50
secondes
; t = 50
secondes
4°) e = vot +![]() a t2 ; e = 20
a t2 ; e = 20![]() 50 +
50 + ![]()
![]() (-0,40)
(-0,40) ![]() 502
502
e = 1000-500
= 500 mètres