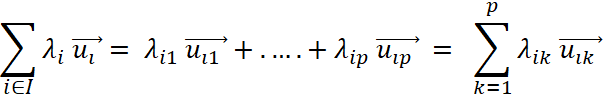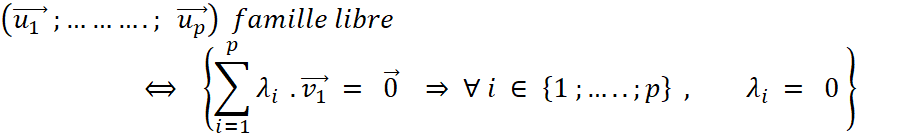Pré requis

Structures algébriques. Sur LES GROUPES , ANNEAUX , CORPS.

ENVIRONNEMENT du dossier

INDEX « warmaths »

Objectif précédent : 1°)Le vecteur 2°) Calcul de la mesure algébrique d’un bipoint

Objectif suivant  1°) les vecteurs colinéaires 2°) le produit scalaire de deux vecteurs.

Info générales : Liste des cours sur le « repérage » Liste des cours sur les vecteurs.

DOSSIER les vecteurs  : Les Espaces vectoriels, et Algèbre.

I ) Les espaces vectoriels.

A ) VECTEUR.

B ) ESPACE VECTORIEL .

C ) SOUS - ESPACE VECTORIEL.

II ) Algèbre.

A ) Familles génératrices ; familles libres et bases.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

	COURS
	Normes sur un espace vectoriel . Topologie .
	Préalable : dans ce cours la lettre « E » est un espace vectoriel . ( pour info plus sur la définition d’un espace vectoriel )
A-	Vecteurs ; Espaces vectoriels ; sous espaces vectoriels.
	Par définition :
	v Un élément de l’ensemble est appelé un vecteur de l’ensemble , les nombres s’appellent les « coordonnées canoniques du vecteur » .
	v Pour une valeur de « i » le vecteur ( lire : vecteur « e » indice « i » ) est le vecteur dont toutes les coordonnées sont nulles à l’exception de la coordonnée coordonnée qui vaut « 1 ». Remarque : Le vecteur nul est le vecteur dont toutes les coordonnées sont nulles ne soit :
	v Soient et deux vecteurs de et soit un nombre ( lire : un nombre alpha appartenant à l’ensemble des nombres )
	Somme de deux vecteurs : La somme ……de et de est définie par : ) , ), ) ) Remarque : les coordonnées de la somme aura pour coordonnées pour chaque rang la somme des coordonnées de même rang ) On écrira plus simplement : , ,
	Il en sera de même pour la somme de 3 vecteurs , et ………….. ainsi de suite ………………………
	INOFO PLUS : voir le représentation graphique d’un vecteur : Coordonnées cartésiennes : -Sur une droite.. ( repère : une dimension…) -Dans un plan.( repère :deux dimensions…) -Dans l’espace ( repère : trois dimensions ..) Voir : un autre repérage dans l’espace….
	Définition : suite.
	La multiplication ( dit aussi produit ) scalaire de par un nombre ( lire nombre alpha ) est définie par : ( à savoir )
	Propositions : eV 1
	Groupe commutatif : L’ensemble muni de la loi de l’addition ( ) : ( ) est un « groupe commutatif » .
	Pour la flèche Lire : « à pour image »
	« élément neutre et opposé ».
	( à savoir ) L’élément neutre pour ( )  est le vecteur : et l’inverse pour appelé « opposé » du vecteur est le vecteur «  ».
	La multiplication (produit par …) par un scalaire.	Info avant ….
	La multiplication par un scalaire : définie par ( ) vérifie les quatre propriétés suivantes :
	Traduction : quel que soit les nombres alpha et béta appartenant à l’ensemble des réels et quelque soit les vecteurs « u » et « v » appartenant à l’ensemble des vecteurs.
	1°)
	2°)
	3°)
	4° ) ( )
B-	ESPACE VECTORIEL .
	Définition :
	Un espace vectoriel « E » sur un corps est un ensemble dans lequel il existe une loi de composition interne , une application , notée «  » , de , et une loi interne , une multiplication par un scalaire , notée Plus précisément :
	v « E » muni de «  » est un groupe commutatif : «  » est associative , commutative , possède un élément neutre , et tout vecteur possède un inverse pour «  » appelé « opposé ». v Les lois ( addition ) «  » et (produit) « » vérifient les propriétés suivantes : La loi « » est une action de : (relation 2°) : Les additions dans sont distributives par rapport à la multiplication scalaire : , - - (relation 3°) - ( la relation 4° ) ( )
	Propositions : eV 2
	est un sous espace vectoriel sur le corps
C-	SOUS - ESPACE VECTORIEL . (noté : sev)
	Définition :
	Un sous espace vectoriel ( sev) d’un espace vectoriel « E » sur le corps est un sous ensemble « F » de « E » vérifiant les trois propriétés suivantes :
	1°) 2°) , ; 3°) , , .
	Remarques : Il est possible de résumer les conditions « 2° » et  « 3° » en . , .
	· Par suite , un sous espace vectoriel « F » et « E » est un sous –ensemble non vide de « E », car il contient , stable par combinaison linéaire : toute combinaison linéaire d’éléments de « F » appartient à « F ».
	· Un sous- espace vectoriel « F » d’un espace vectoriel « E » sur le corps est également un espace vectoriel sur le corps . · Les sous espaces vectoriels sont les généralisations en dimension quelconque des droites et des plans . · Pour tout et sont des sous-espaces vectoriels de . · Pour montrer qu’un ensemble « F » est un espace vectoriel sur le corps « K » , il est souvent beaucoup plus rapide de montrer qu’il est un sous-espace vectoriel d’un ensemble que nous savons déjà être un espace vectoriel sur le corps « K ».
	II ) Algèbre.
	Définition : Une algèbre sur un corps commutatif est une structure algébrique ( telle que : · ( est un espace vectoriel sur  ; · La loi «  » est des dans , c’est une loi de composition interne ; · La loi est distributive par rapport à la loi  ; · Pour tout dans et pour tout dans ,
	Exemple : est une algèbre sur de dimension « 2 ». Si est un corps commutatif , est une algèbre sur .
	A ) Familles génératrices ; familles libres et bases.
	Définition. Soit I un ensemble , E un espace vectoriel sur le corps , une famille de vecteurs de E et une famille d’éléments de Presque tous nuls, c'est-à-dire tous nuls sauf éventuellement un nombre « p » fini d’entre eux. Nous appelons combinaison linéaire de vecteurs de la famille de coefficient la somme : Où les : , , sont les seuls éléments de « I » pour lesquels
	Définition : Soit un ensemble , un espace vectoriel sur le corps , une famille de vecteurs de . Un vecteur est une combinaison linéaire des vecteurs de la famille s’il existe une famille d’éléments de presque tous nuls, telle que «  » est la combinaison linéaire de vecteurs de la famille de coefficient .
	Définition : Soit un ensemble , un espace vectoriel sur le corps , une famille de vecteurs de et un sous ensemble vectoriel ( sev) de . · est une famille génératrice de si tout élément de s’écrit comme une combinaison linéaire des vecteurs de la famille . · Les éléments de , presque tous nuls , . qui interviennent dans l’écriture de « u » comme combinaison linéaire des vecteurs de la famille sont des coordonnées de dans la famille . · Si .est une famille génératrice de , alors nous disons que est engendré par
	Définition : Les vecteurs .forment une famille libre de si et seulement si aucun des vecteurs de . ne peut être obtenu comme combinaison linéaire des autres vecteurs de cette famille.
	Définition : Si les vecteurs .ne forment pas une famille libre, nous disons que les vecteurs sont liés.
	Proposition 7 : avec les notations de la définition précédente , nous avons :
	Définition : Si une famille génératrice de , un sev de . Nous dirons que est une base de si est à la fois une famille libre et génératrice de .
	Proposition 8 : Soit l’ensemble un sous ensemble vectoriel ( sev) d’un espace vectoriel sur le corps . Soit une base de . Tout vecteur s’écrit de manière unique comme combinaison linéaire des vecteurs de base . Rn fait, nous avons :

TRAVAUX AUTO FORMATIFS.

CONTROLE

Evaluation .