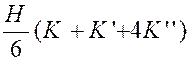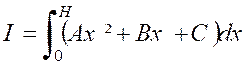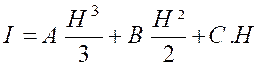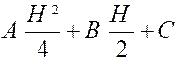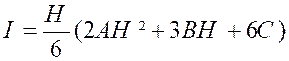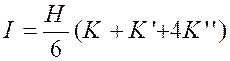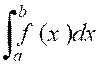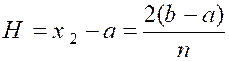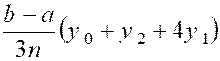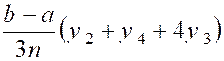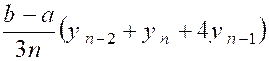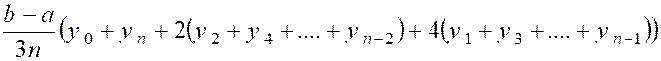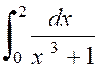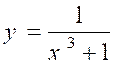COURS

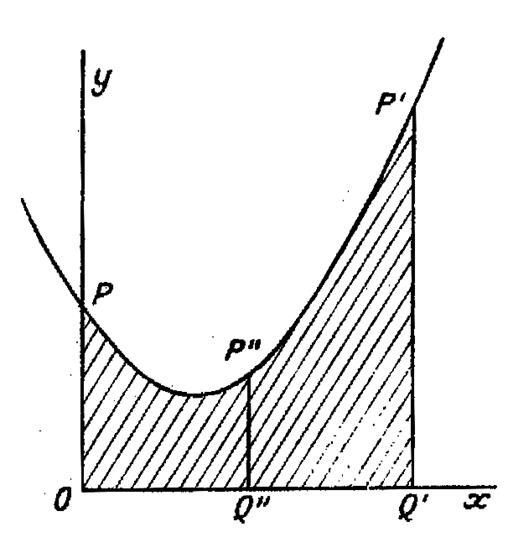
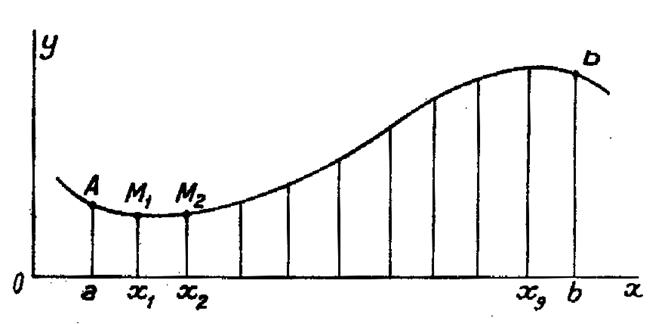
Cette méthode utilise un résultat relatif à l’aire limitée par une parabole « y =A x² + B x+ C »  (voir la figure ci-dessous) l’axe « 0x » et  « O’P’ » .

Posons « OQ’ =H » ; « OP = K » ; « Q’P’ = K’ » , soit «  K ‘’ = Q  ‘’ P ‘’ »  l’ordonnée équidistante des deux autres.
Nous allons démontrer que l’aire «  O P P ‘ Q’ » a pour valeur « 

En effet , cette aire est égale à l’intégrale :

soit 

D’autre part on a :

« K = C »

« K’= A H² + BH + C »

et  «  K’’=  »

On vérifie bien que    = 

Ceci posé, pour trouver une valeur approchée de l’intégrale «  partageons l’intervalle ( a ; b) en un nombre pair de parties, soit «  n = 10 ». (voir ci contre).

Par les trois premiers points « A » ;  « M₁ » ; « M₂ »,nous faisons passer une parabole de la forme précédente .En effet,l’équation de cette parabole contient trois coefficients qui sont déterminés par le fait que cette équation est vérifiée pour les coordonnées des points « A » ;  « M₁ » ; « M₂ ».

L’aire comprise entre la courbe ,l’axe «  » et les deux droites « x = a » et « x= x 2 » diffère  très peu de l’aire obtenue en remplaçant la courbe par la parabole .

Nous avons ici :

lire ci-dessous « B »

Et

D’où une valeur approchée de la surface :  «  »   

  on obtient de même les aires suivantes :

 ;…………………………

En faisant la somme ,on obtient :

La méthode est assez précise,mais ne permet pas d’avoir ni une limite supérieure de l’erreur commise,ni le sens de cette erreur.

Exemple :

Calculer l’intégrale

x

x³

x³+1

0,0

0

1

0,2

0,008

1,008

0,4

0,064

1,064

0,6

0,216

1,216

0,8

0,512

1,512

1

1

2

1,2

1,728

2,728

1,4

2,744

3,744

1,6

4,096

5,096

1,8

5,,832

6,832

2

8

9

En portant ces valeurs dans la formule précédente,on trouve comme valeur approchée : 1,090

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!

EVALUATION :

calculer :

Calculer l’intégrale   en calculant avec la méthode de simpson

Voir le cours !!!!!