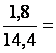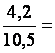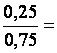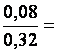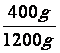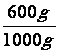|
Module : 6 La fraction. |
DOSSIER : 161 |
|||
|
LOGICIEL warmaths ; Pour Aide et
Formation Individualisée
; REMEDIATION mise à /NIVEAU : niveau VI |
||||
|
TRAVAUX FORMATIFS /
COLLEGE / Lycée Matière :
MATHEMATIQUES.
Niveau VI |
||||
|
CORRIGE SIMPLIFICATION D’UNE FRACTION |
||||
|
|
||||
|
Info 1 @ « cours
sur la simplification de fractions… » ; |
||||
|
TRAVAUX CONTROLE |
||||
|
Les
questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours
. |
||||
Simplifier une fraction, c’est la remplacer par une
fraction égale ayant des termes plus petits (plus simples) il faut pour
cela diviser ses deux termes par
un même nombre.
Multiplier les deux termes d’une fraction, c’est
toujours possible; mais les diviser est-il toujours possible ?
On
peut simplifier :
Mais
peut - on simplifier les fractions :
on ne peut pas simplifier ces fractions……
Quand on ne peut pas (ou ne peut plus) simplifier
une fraction, on dit qu’elle ne plus
être réduite ; on dit qu’elle
est « irréductible ».
1.
Simplifiez
les fractions, en effectuant les calcul indiqués :
( il faut
effectuer les divisions proposées)
|
|
|
|
|
|
|
|
2
. Complétez :
|
Comment
est-on passé de « 24 » à « 4 » ?
|
Comment
est-on passé de « 20 » à « 4 » ?
|
Comment est-on passé de « 14 » à
« 2 » ? on
divise 14 par 2 : on trouve « 7 » ; on divise
« 21 » par « 7 » réponse :
|
|
|
|
|
3. Simplifiez : Rappel : on simplifie une fraction si on divise le
numérateur et le dénominateur par un même nombre entier ; attention :
le numérateur et le dénominateur doivent rester des nombres entiers.
a)
par 2 ; 4 ; 5 ou 10, au choix :
|
|
|
|
|
|
|
On
peut simplifier par : par
2 := |
|
|
|
|
|
on
peut simplifier par : par
2 := |
par
2 := |
par
2 := NON ; par 4 =NON ; par 5 : = |
b )
par 3 ; 6 ou 9, au
choix :
|
par
3 =
|
par
3 =
|
par
3 =
|
|
par
3 =
|
par
3 =
|
par
3 =
|
4. Encadrez
les fractions irréductibles. Simplifiez les autres jusqu’à ce qu’elles soient
irréductibles.
|
|
Ne
peut être simplifiée Elle
est irréductible |
|
Simplification :
Elle
est irréductible |
|
Ne
peut être simplifiée Elle
est irréductible |
|
|
Simplification :
soit
= Fraction
irréductible |
|
Elle
est irréductible |
|
Simplification : Fraction
irréductible |
|
|
Ne
peut être simplifiée Elle
est irréductible |
|
|
|
|
|
|
Simplification :
|
|
Ne
peut être simplifiée Elle
est irréductible |
|
|
5
. Quelle fraction de litre est contenue
dans une bouteille de 40 cL ?
Écrivez-la,
puis simplifiez-la; retrouvez ensuite la valeur décimale de la fraction. = 
; la valeur
décimale est de : 0,40 litre
Même
question
·
pour des bouteilles de 75 cL;
: 
la valeur décimale est
de : 0,75 litre
·
pour des bouteilles
de 80 cL. : 
la valeur décimale est
de : 0,80 litre
6. Dites quelle fraction
d’heure représentent :
15
mn; 20 mn; 30 mn; 40 mn; 45 mn; 12 mn; 5 mn; 10 mn. Simplifiez s’il y a lieu.
|
15 mn; |
|
20 mn |
|
30 mn |
|
40 mn |
|
45 mn; |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 mn |
|
5 mn |
|
10 mn |
|
|
|
|
|
7. Simplifiez les écritures fractionnaires suivantes, après en avoir rendu les
termes entiers :
0,9 3,6 1,8 4,2 0,25 0,08
2,4 8,4 14,4 10,5 0,75 0,32
|
|
On
multiplie en haut ( num.) et en bas (dén.)
par 10
|
|
On
multiplie en haut ( num.) et en bas (dén.)
par 10
|
|
On
multiplie en haut ( num.) et en bas (dén.)
par 10
|
|
|
|
|
|
|
|
|
|
On
multiplie en haut ( num.) et en bas (dén.)
par 10
|
|
On
multiplie en haut ( num.) et en bas (dén.)
par 100
|
|
On
multiplie en haut ( num.) et en bas (dén.)
par 100
|
8.
Un pot-au-feu de
|
|
Fraction
de la masse totale représente la masse d’os |
|
|
|
|
|
Simplification :
|
|
|
|
|
|
|
9
. Un kilogramme de cerises donne
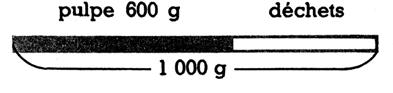
Quelle fraction du poids total représente la
masse de pulpe ? Simplifiez-la le plus
possible.
|
|
Fraction
de la masse totale représente la masse d’os |
|
|
|
|
|
Simplification :
|
|
|
|
|
|
|
10 ) Une
ménagère a acheté
a)
Quelle masse de pulpe aura-t-elle ? les « 3 / 5 » de 12
kg : soit 0,6 de 12 kg = 7,2 kg
de pulpe.
b) A quel prix lui revient
Coût des cerises : 12 fois 1,30 = 15,6
€ ;
Prix de revient d’un kg de pulpe : 15,6 / 7,2
= 2,16 €