|
Devoir
sommatif sur : TRACES
( I ) et
CARACTERISTIQUES (II) sur LES QUADRILATERES |
||
|
|
|
|
|
|
>>>> DEVOIR et
Evaluation Géométrie CC |
I ) EXERCICES DE CONSTRUCTION :
Les @ parallélogrammes
|
1°) Tracer un :Parallélogramme ABCD de côtés AB = 35 mm et AD = 45 mm et |
|
|
2°) Tracer un :
Parallélogramme ABCD tel que AB = 26
mm et AD = 48 mm et la diagonale BD = 40 mm |
|
|
3°) Tracer un :Parallélogramme ABCD
de côté AB = 5cm et de diagonales AC = 4 cm et BD = 80 mm |
|
|
4°) Tracer un :Parallélogramme
ABCD tel que AB = 2,5cm et AD = 5cm et la diagonale AC = 64 mm |
|
|
5°) Tracer un :
Parallélogramme ABCD de côtés AB = 5cm et AD = 4cm et de hauteur AH = 3cm |
|
|
6°) Tracer un :Parallélogramme ABCD de côté AB = 30 mm et de
hauteurs AH = 25 mm et AK = 32 mm ( niveau +++) |
|
|
1°) Tracer un :Rectangle ABCD tel que
AB = 55mm et AD = 35 mm |
|
|
2°) Tracer un :Rectangle ABCD de
diagonale 5 cm et de côté AB = 20 mm |
|
|
3°) En +++ : Tracer un : Rectangle ABCD de diagonale 55 mm et tel que |
|
|
4°) En plus : Tracer un : rectangle ABCD de
longueur triple de la largeur et de périmètre 16 cm . |
|
|
1°) Tracer un :Losange ABCD tel que AB
= 27 mm et |
|
|
2°) Tracer un :Losange ABCD de
diagonales AC = 46 mm et BD = 38 mm |
|
|
3°) Tracer un : Losange ABCD
de diagonale BD = 4 cm et tel que |
|
|
4°) Tracer un :En plus : losange
d’aire A = 6cm2 et de
diagonale AC = 3 cm |
|
|
1°) Tracer un :Carré de côté AB = 43 mm |
|
|
2°) Tracer un :Carré de diagonale AC =
52 mm |
|
|
4°) Tracer un :En plus : carré de
périmètre p = 10 cm |
|
|
5°) Tracer un :En plus : carré
d’aire A = 1225 mm2 |
|
|
II ) contrôle des CONNAISSANCES : Exercices d’identification : Soit le parallélogramme ABCD et « O »
le point d’intersection des diagonales |
|
Consignes : mettre une croix
pour les figures concernées ; justifier.
|
Propriétés ou caractères |
trapèze |
Trapèze
isocèle |
Trapèze
rectangle |
parallélogramme |
rectangle |
Losange |
Carré |
justification |
AB // DC
|
|
|
|
|
|
|
|
|
|
AO =OC= OD = OB |
|
|
|
|
|
|
|
|
|
AB = BC=CD=DA |
|
|
|
|
|
|
|
|
|
AB//DC et |
|
|
|
|
|
|
|
|
|
BC // AD et |
|
|
|
|
|
|
|
|
|
AB = CD et AD = BC |
|
|
|
|
|
|
|
|
|
Rectangle et AB = BC |
|
|
|
|
|
|
|
|
|
Parallélogramme tel que AC ^ BD |
|
|
|
|
|
|
|
|
|
Propriétés ou caractères
|
trapèze |
Trapèze
isocèle |
Trapèze
rectangle |
parallélogramme |
rectangle |
Losange |
Carré |
justification |
|
AD // BC et |
|
|
|
|
|
|
|
|
|
AB //CD Et AD // BC |
|
|
|
|
|
|
|
|
|
Losange tel que |
|
|
|
|
|
|
|
|
|
AB //DC et AB =DC=BC |
|
|
|
|
|
|
|
|
|
Médiatrice de
AB et médiatrice de DC confondues |
|
|
|
|
|
|
|
|
|
AB // CD et AB = CD |
|
|
|
|
|
|
|
|
|
[AC] et [BD ]
médiatrices l’une de l’autre |
|
|
|
|
|
|
|
|
|
AD // BC et AB = CD |
|
|
|
|
|
|
|
|
|
m(A,C) = m (
B,D)= 0 |
|
|
|
|
|
|
|
|
|
Propriétés ou caractères
|
trapèze |
Trapèze
isocèle |
Trapèze
rectangle |
parallélogramme |
rectangle |
Losange |
Carré |
justification |
|
Losange tel que
AC = BD |
|
|
|
|
|
|
|
|
|
m(A,C) et m (B,D) = 0 et AC = BD |
|
|
|
|
|
|
|
|
RESUME de cours :
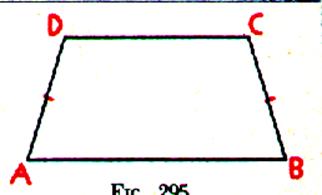
Les 3 Différentes sortes de trapèze :
|
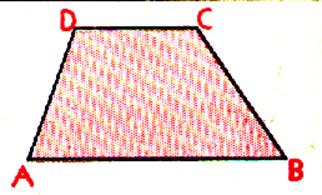
1°)Trapèze quelconque |
|
|
Définition description : - Quadrilatère convexe ayant deux côtés parallèles .
[DC] // [AB] - [DC] et [AB]
sont les bases. AB > DC [DC] est la plus petite base et
[AB] est la plus grande base. |
|
|
Propriétés:
les angles ayant pour
sommets les extrémités d’un des côtés non parallèles sont supplémentaires .
Identification : Quadrilatère convexe ayant deux côtés parallèles . [DC]
// [AB] |
|
|
2°) Trapèze
isocèle |
|
|
C’est un trapèze dont les cotés non
parallèles sont isométriques. (1) AD = BC
|
|
|
-Propriétés du trapèze quelconque -les angles à la base sont égaux - les
médiatrices des bases sont confondues ( 3) - l’axe de
symétrie : médiatrice des bases - l’identification
se fait avec (1) ou (2) ou
(3) |
|
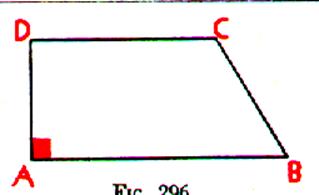
3°)Trapèze
rectangle DCBA
|
|
|
Description : Trapèze ayant un angle droit
|
|
|
Propriétés : - propriétés du
trapèze quelconque - si Identification à partir
de : Trapèze ayant un angle droit |
|
LE PARALLELOGRAMME