calculs de la distance de deux points dans un repere orthogonal

	Classe de troisième de collège..		Programme de 3^ème

	Fiche pédagogique à travailler….		Aller au corrigé !!!!!

Pré requis:

Projection orthogonale d’un segment (détermination des composantes)
Mesure algébrique d’un bipoint .
DISTANCE entre deux points .

ENVIRONNEMENT du dossier:

Retour vers la page entrée warmaths

Objectif précédent :

1°)Composantes d’un segment

2°) Coordonnées d’un vecteur dans un repère

Objectif suivant :

Calcul de la longueur d’un segment dans un plan

Liste des cours sur la géométrie.

	Fiche : Distance de deux points dans un repère orthonormal.

	Rappel : repère orthonormal et repère orthogonal.
	I ) Distance d’un point à l’origine ( repère orthonormal)
	II ) Distance de deux points quelconques du plan .( dans un repère orthonormal)
	III ) Exercices types.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Vocabulaire : Un repère est constitué par 2 axes de coordonnées de même origine. Un repère orthogonal : un repère orthogonal à ses deux axes perpendiculaires . ( on ne parle pas de ses unités ) Un repère orthonormal : un repère est orthonormal di les deux axes sont perpendiculaires et ont même unités de longueur sur les axes.

I ) Distance d’un point à l’origine ( repère orthonormal)
Dans les 4 cas ci-dessous , vous allez calculer la distance d’un point à l’origine « O ». Pour cela , vous faites apparaitre un triangle rectangle ( coloriez –le) et vous appliquez le théorème de Pythagore.
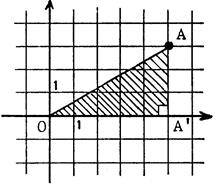
Cas 1
OA² = OA’ ² + A’ A ² OA² = 5² + 3 ² OA² = 25 + 9 OA² = 34 OA = qui s’écrit aussi : OA =
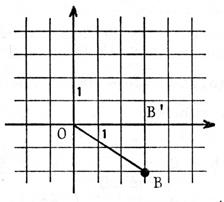
Cas 2 :
OB² = OB’ ² + B’B² OB² = 3² + 2² OB² = 9 + 4 = 13 OB = soit :
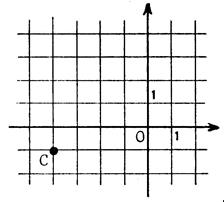
Cas 3 :
OC² = ……OC’²……..+ ……C’C²….. OC² = ……1²……. + ……4²…… OC² = ……17……….. OC = ……………
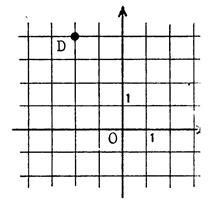
Cas 4 :
OD² = ……OD ‘²……..+ ……D’D²….. OD² = ……4²……. + ……2²…… OD² = ……20……….. OD = ……………

Or vous savez que : « Deux nombres opposés ont le même carré ». Exemple ( - 4 ) ² = 4² (info +++@)
Vous pouvez donc , dans vos calculs , faire apparaitre les coordonnées des points « A ; B ; C ; D ». Ainsi si nous reprenons les 4 cas précédents.

Cas 1 :	Cas 2 :	Cas 3 :	Cas 4 :
A ( 5 ; 3 ) OA² = 5 ² + 3 ²	B ( 3 ; -2 ) OB² = 3² + ( -2 )²	C ( -4 ; -1 ) OB² = ( - 4 ) ² + ( -1 )²	D ( -2 ; 4 ) OD² = OD’² + D’D ² OD² = 4 ² + ( -2 )²

Dans tous les cas , vous constatez que le carré de la distance d’un point à l’origine est égal à la somme des carrés des coordonnées du point. On énoncera alors :
Le théorème : Le plan étant muni d’un repère orthonormal d’origine « O ». Si « M ( m ; m’) » alors OM² = m² m’² ou encore « OM = » ; qui peut s’écrire aussi :

Activité 1 : Le plan est muni d’un repère orthonormal d’origine « O » , « P ( ) ». On vous demande de calculer : OP . ( la distance de O à P)

II ) Distance de deux points quelconques du plan .( dans un repère orthonormal)

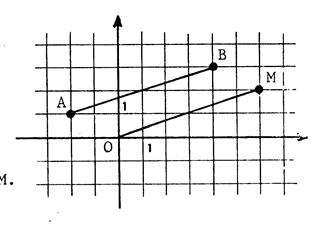
Soit la figure ci-contre : Sur cette figure on a placé les points A ( -2 ; 1 ) et B ( 4 ; 3 ). Nous allons choisir de calculer la longueur « AB »
« M » est l’image de « O » dans la translation de vecteur . On a alors et par conséquent « OM = AB » Les coordonnées de sont égales aux coordonnées de « M ». ; soit 6 ; 2 ) D’après ce qui précède , OM² = 6² + .. 2².. = 40 donc AB = .
Cas général : Dans le plan muni d’un repère orthonormal, considérons les points A ( x , y ) ; B ( x’ ; y’ ). En raisonnant comme précédemment on a y’ – y )²

Théorème : Le plan étant muni d’un repère orthonormal , Si A ( x , y ) et B ( x’ ; y’ ) alors AB² = ( x’ – x )² + ( y’ – y )² ou

III ) Exercices types.
Avertissement : Dans toutes les activités proposées , le repère est orthonormal .

Activité 1 : soit M ( - 8 ; 3 ) et N ( 4 ; -2 ) . Calculez « MN » . ( utilisez le théorème vu précédemment )

Activité 2 :
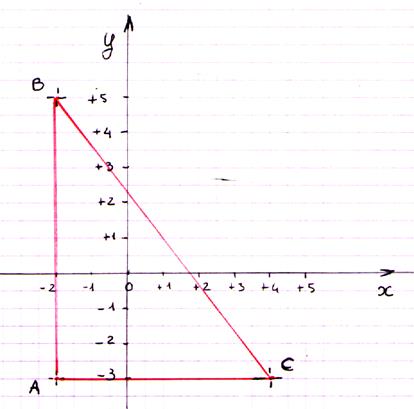
Sur la figure ci-contre : Placez les points H( 1 ; 4 ) ; K ( 7 ; - 2 ) ; L ( -3 ; - 6 ). Démontrez que « HKL » est un triangle isocèle.
Activité 3 :
Sur la figure ci-contre : Placez les points E ( 4 ; -2 ) ; D ( 0 ; 6 ) ; F ( 0 ; - 4 ) ; Démontrez que « EDF » est un triangle rectangle.
Activité 4 :
Sur la figure ci-contre : Placez les points : A ( 3 ; 5 ) ; B ( 2 ; -3 ) ; C ( -5 ; - 7 ) ; D ( -4 ;1 ) . Démontrez que « ABCD » est un losange.
Activité 4 :
Placez les points A ( -3 ; 3 ) et B ( 4 ; -1 ) Soit C ( x ; -3 ) . ON se propose de déterminer l’ abscisse « x » du point « C » de telle sorte que le triangle « ABC » soit rectangle ( en « A » , « B » ou « C » ). Tous les points qui ont pour ordonnée « -3 » sont situés sur une parallèle à l’axe des abscisses . Tracez – la . Les points « C » cherchés sont situés sur elle.
1°) Déterminez par le dessin les points « C » possibles. ( Si les triangle est rectangle en « C » ; « C » est sur le cercle de diamètre )

2°) Déterminez par le calcul les coordonnées des points « C » qui conviennent . ( A rédiger sur une autre feuille )