DOSSIER :Le théorème de PYTHAGORE

Fiche 1 / Le théorème de Pythagore. ( Démonstrations).

Fiche 2 : Application du théorème de Pythagore .

Fiche 3 : Calculs dans l’espace.

Fiche 4 : Réciproque du théorème de Pythagore.

Fiche 5 : Exercices.

Fiche 1. Le théorème de Pythagore.

Les constatations que vous avez faites dans le cours sur « le triangle rectangle » à une propriété sous le  nom de « Théorème de Pythagore ».

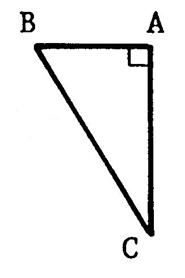
d’où le théorème « 10 ». 

Si « ABC » est un triangle rectangle en « A » alors : 

BC²  = BA² + AC²

Par abus de langage , au lieu de « carré de la mesure de la longueur du côté »  on dit « carré du côté » ( de même pour l’hypoténuse) .

Avec ces notations , on dira :

Théorème de Pythagore :

Dans tout triangle rectangle le carré de l’hypoténuse est égal à la somme des carrés des deux autres  côtés.

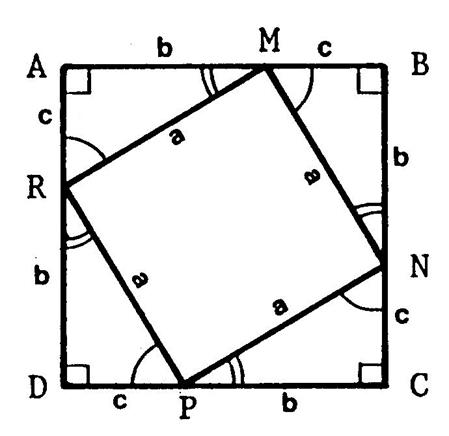
Démonstration :

« ABCD » est un carré.

Sur les côtés de ce carré , on a placé les points « M », »N » , « P » , « R »  tels que « AM = BN= CP= DR= b »  et  «  MB = NC = PD = RA = c ».

Les triangles  "ARM" , "BMN » ,  « CPN » et « DPR » sont superposables.

( Ce sont les moitiés de rectangles dont les côtés ont pour longueur « b » et « c » )

Appelons « a » l’hypoténuse de ces triangles rectangles :

«  MN = NP = PR = RM = a »

Le quadrilatère « MNPR » dont les côtés ont la même longueur est un ……..losange…….

Dans tous les triangles rectangles , les angles aigus sont complémentaires et comme les 4 triangles sont superposables , alors ( par exemple)  et    sont complémentaires donc   est ……… « droit »………………..

Donc , le losange « RMNP » qui a un angle droit est un   carré dont le côté est « a ».

Sur les deux figures suivantes on a représenté le même carré « ABCD »

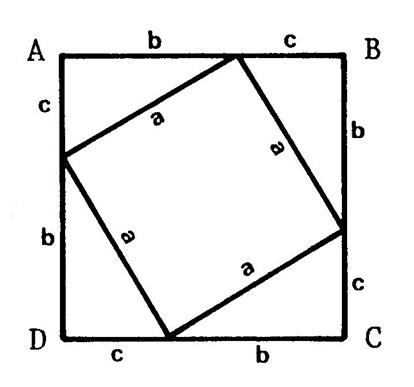
Figure 1

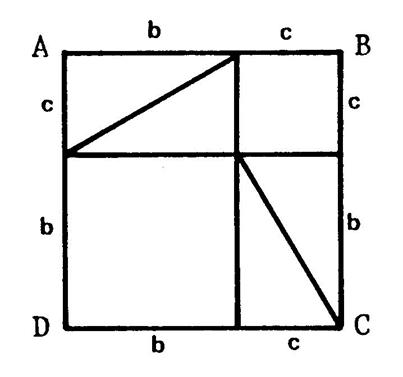
Figure 2

Mais vous remarquez que les 4 triangles sont disposés différemment.

Activité :

Passez en couleur les 4 triangles sur les deux figures.

La surface non colorée dans le carré « ABCD » a la même aire dans les deux figures.

Sur Figure 1  , c’es un carré de côté « a » , son aire est « a² ».

Sur la figure 2 , ce sont deux carrés de côtés respectifs « b » et « c », l’aire est donc «  b² + c² »

L’aire étant dans les deux cas , on peut donc écrire : «  a² =  b² + c² »

v Nous vous proposons une autre démonstration :

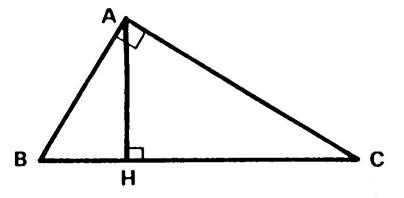
« ABC » est un triangle rectangle en « A3. [AH] est la hauteur.

Par définition , on peut écrire :

De même , dans le triangle rectangle « BAH »,

Donc , par transitivité,   c'est-à-dire        d’où     (rel.1 )

Dans le triangle rectangle «  ABC » ,    , de même , dans le triangle « CAH »    ,

Donc ,par transitivité ,    , c'est-à-dire     d’où     (rel.2 )

« H » est situé entre « B » et « C » ( on peut le démontrer )  donc 

Alors grâce aux égalités des deux relation ( rel. 1 et rel.2) , on peut écrire que :

C'est-à-dire : 

On en déduit que    , c'est-à-dire que  

Fiche 2 : Application du théorème de Pythagore .

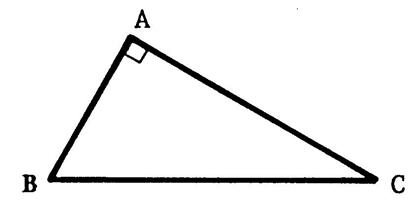
« ABC »  est un triangle rectangle en « A ».

Nous allons comparer l’hypoténuse aux deux autres côtés.

D’après le théorème de Pythagore :  

On en déduit alors que  

Vous savez que deux nombres positifs sont rangés dans le même ordre que leurs carrés ( vous leçon :…….Fiche :    .)

Donc 

Théorème n°11 :

Dans tout triangle rectangle, l’hypoténuse est le plus grand des côtés.

Activités :

Calcul de longueurs dans un triangle rectangle.

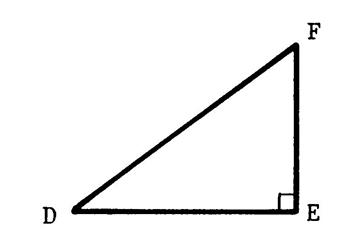
Exercice 1 :

« DEF » est un triangle rectangle en « E ».

L’unité est le « cm. »

Sachant que  « DE = 8 »  et « EF= 6 ». Vous devez calculer « DF ».

Résolution :

Grâce au théorème de Pythagore , on peut écrire

On a alors   d’où     

Puisque     ;    

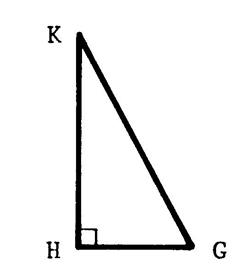
Exercice 2 :

« HKG » est un triangle rectangle en « H ».

L’unité est le « cm. »

Sachant que  « GK = 17 »  et « HK = 15 ». Vous devez calculer « GH ».

Résolution :

Grâce au théorème de Pythagore , on peut écrire

On a alors en déduit      d’où     

    ;        ;alors    

Exercice 3 :

Dessinez un triangle « MNP » rectangle en « P » sachant que  ( en mm) , « MP = 55 »  et «  PN = 35 ».

Ci-contre , le côté   [NP] est déjà placé.

1°) Calculez une valeur approchée de « MN »  ( à 1 mm près)

2°) Calculez une valeur approchée ( à 1° près) de .

Contrôlez en mesurant sur la figure.

Exercice 4 :

( sur feuille)  Dessinez un triangle « RST » rectangle en « T » sachant que ( en mm) «  RS = 100 » et « RT = 60 ».

Le côté [RS] est déjà placé. ( voir la fiche 3 : sur le triangle rectangle).

Tracez la hauteur [TV].

1°) Calculez « TS ».

2°) En utilisant l’aire de  « RST » , calculez « TV ».

3°) Calculez « RV » et « VS ».

Contrôlez en mesurant sur la figure.

Fiche 3 : Calculs dans l’espace.

Info +++ sur..

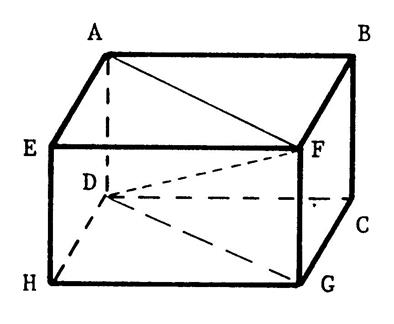
« ABCDEFGH » est un parallélépipède rectangle tel que  ( en cm) « AB= 12 , « BF= 9 » , « BC = 8 ».

Vous allez calculer « DF » . Pour cela :

Expliquez (oralement) pourquoi « AFGH » est un rectangle .

Commencez par calculer « AF »  

Fiche 4 : Réciproque du théorème de Pythagore.

Voici trois nombres « 33 » , « 56 » , « 65 ».

Calculez leurs carrés.

33² =  1089

56 ² =    3136

65 ² = 4225

Complétez :   33²   + 56 ²  = 1089   +   3136    =  4225

Vous constatez que   33²   + 56 ²  =  65²

    Construisez un triangle dont les longueurs des  côtés ( en mm) sont  « 33 » , « 56 » , « 65 ».

Que constatez-vous pour ce triangle ?........................................................................................

    Ce que vous venez de constatez , il est possible de le démontrer , nous l’admettrons:

Propriété 38 :

Si dans un triangle le carré d’un des côtés est égal à la somme des carrés des deux autres côtés, alors le triangle est rectangle.

Remarque : étant donné un triangle « ABC » dans lequel « BC » est le plus grand côté, si    , alors le triangle  « ABC »  n’est pas rectangle.  ( expliquez verbalement )

Exercice 1 : On donne un triangle « MNP » tel que  ( en cm) « MN= 85 » , « PN = 84 » , «  PM = 13 ».

1°) Démontrez que « MNP » est un triangle rectangle.

2°) Soit  « R » un point tel que « MR = 36 » et « NR = 77 ».

                                Démontrez que « R3 est situé sur le cercle circonscrit au triangle « MNP »

Exercice 2 : Dessinez un rectangle « ABCD » tel que  ( en mm) « AB = 60 »    et  « BC = 30 ».

Placez    sur  [AB] un point « P » tel que « AP = 40 ».

Tracez  [DP]  et  [PC]

Faites  les calculs nécessaires pour savoir si le triangle   « DPC » est rectangle ou  non.

Fiche 5 : Exercices

Exercice 1 :

 ABCD est un losange  de centre 0 tel que AC = 80 et BD = 18 Calcule la longueur des côtés de ce losange, (unité le mm)

Exercice 2 : On donne un cercle de centre 0 et de rayon R = 26 (unité le mm) . [EF] est une corde telle que EF = 48. G étant le projeté de 0 sur (EF), calcule OG.

Exercice 3  On donne deux demi-droites [Ox et [Oy telles que  soit aigu, cos    = 0,8.

1 °) Faites la figure en expliquant la construction.

                                       (Cette figure sera complétée tout au long du problème).

 2°) Soit M un point de [Ox tel que (en mm) OM = 45.

                             Soit H le projeté orthogonal de M sur [Oy. Calculez OH et MH.

 3°) Soit P le point de [OM] tel que OP = 2 PM . Calculez  OP et PM.

 4°) Soit K le projeté orthogonal de P sur [Oy.  Calculez  OK , KH , PK.

 5°) Calculez  PH. Donnez  une valeur approchée de PH à 0,1 près.

 6°) Dites en l'expliquant si OPH est un triangle rectangle.

Exercice 4 :

« ABC »   est un triangle rectangle en A de hauteur [AD] . AB = 15 et AC = 20. (unité le  cm).

 « E » est le projeté orthogonal de D sur (AC) et « F » le projeté orthogonal de D sur (AB).

 Calculez     BC , AD , BD , DC , ED , FD , AF , AE , FB , EC , EF.

 (il sera parfois utile de faire intervenir des calculs d'aires).

Exercice 5

RST est un triangle tel que RS = 25 et ST = 17 (unité le cm). [SJ] est hauteur. J est un point de [RT]. SJ = 15. Faites les calculs nécessaires pour savoir si RST est oui ou non rectangle en S.

Exercice 6

On donne deux points M et N tels que MN = 10 (unité le cm).

On trace le cercle de centre M et de rayon 8 et le cercle de centre N et de rayon 6.

Les deux cercles se coupent en E et F.

1°) Démontrez que MEN et MNF sont des triangles rectangles.

 2°) Démontrez que (MN) est médiatrice de [EF].

3°) (MN) et (EF) se coupent en L. Calculez EF. (utilise le calcul d'aire).

Exercice 7 d'après BEPC AMIENS, Juin 87.

PQRS est un rectangle. PQ = 3, QR = 5 (l'unité est le cm).

E est un point de la demi-droite [QR.

 Faire une figure dans chacun des cas suivants.

 1°) On suppose que QE= 2. Calculez PE (donnez une valeur approchée à 0,1 près).

2°) On suppose que  = 45°. Calculez QE et PE (donnez une valeur approchée à 0,1 près)

 3°) On suppose que le triangle SPE est isocèle de sommet principal P. Calculez QE.

4°) On suppose que " « 60°. Calculez  PE et QE (donnez une valeur approchée à 0,1 près)

Exercice 8

 ABCD est un carré dont le côté est égal à 100 mm . M est le milieu de [BC].

1° ) P est le point de [DC] tel que DP « 70 mm . Faites une figure.

Faites les calculs nécessaires pour savoir si le triangle AMP est rectangle ou non.

 2°) En faisant une figure soignée, cherchez où il faudrait placer un point N sur [ DC], pour que le triangle AMN soit rectangle en M (mesure DN). Vérifiez par le calcul la valeur trouvée pour DN.

CONTROLE