Pré requis :

Géométrie : le quadrillage

Environnement du dossier

Index warmaths

Objectif précédent : Fonction linéaire

Objectif suivant : l’échelle

Info Plus :

DOSSIER Les cartes géographiques

LES CARTES ROUTIERES et échelles graphiques

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
				Vers des travaux en arithmétique

COURS

Définitions de l’échelle :

Observation :

Observons deux épreuves de format différent d’une même photo.

a) sur les deux épreuves , les angles formés par deux lignes analogues (en géométrie on dit « homologues » ) représentant les mêmes lignes réelles , sont égaux .

b) Au contraire , les longueurs analogues sont modifiées .

Ainsi : chaque longueur « ab » d’une épreuve s’obtient en multipliant la longueur « AB » correspondante de l’autre épreuve par un même nombre ou une fraction quelles que soit ces longueurs .

Ce nombre s’appelle « échelle » , ou « rapport de réduction » ou « rapport d’agrandissement » ou « rapport de similitude »

Echelles :

Par exemple , pour reproduire un dessin à l’échelle ½ , il faut multiplier toutes les longueurs par ½ (ou 0,5) ; pour reproduire un dessin à l’échelle 3 , il faut multiplier toutes les longueurs par 3 , les angles de la figure restant inchangées.

L’échelle s’exprime aussi par un nombre décimal. Par exemple , pour reproduire un dessin à l’échelle 2,5 , il faut multiplier toutes les longueurs par 2,5 .

On dit aussi , par exemple , qu’un terrain est reproduit à l’échelle de 1cm par mètre. .Cela signifie qu’une longueur vraie de 1m est représentée sur le dessin par 1 cm. Inversement , si on mesure une longueur de 1 cm sur le dessin , c’est que la vraie longueur est 1 m . L’échelle de réduction est égale à 1 /100 .

Il est commode de donner l’échelle sous forme d’une fraction ou d’un nombre décimal .

Si l’échelle est 5/7 par exemple , cela signifie que 7 cm vrais sont représentés sur un dessin par 5 cm, que 7 m sont représentés par 5 m , , que 7 mm sont représentés par 5 mm …..

Si l’échelle est 0,5 par exemple , cela signifie que 1 m vrai est représenté par 0,5 m ; c’est à dire 5 dm , que 1 cm est représenté par 0,5 cm , c’est à dire 5 mm, que 1 mm est représenté par 0,5 mm , c’est à dire un demi millimètre.

Cartes couramment utilisées:

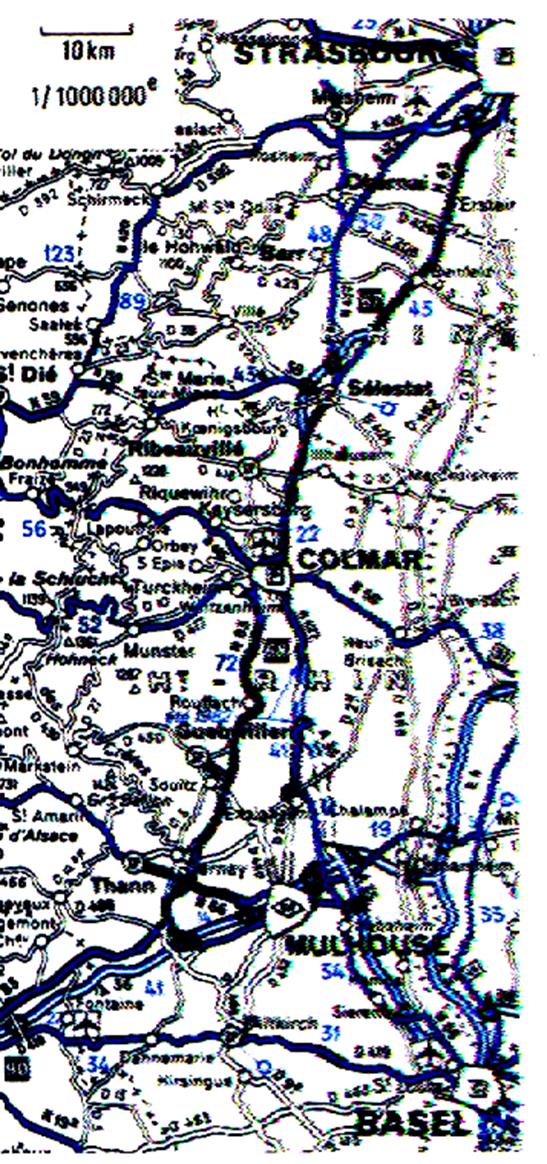
Cartes routières au 1 / 1 000 000 Une longueur de 1 000 000 cm sur le terrain est représentée par 1 cm sur la carte. 1cm sur la carte représente donc 10 km sur le terrain.
Cartes routières au 1 / 100 000 Une longueur de 100 000 cm sur le terrain est représentée par 1 cm sur la carte. 1cm sur la carte représente donc 1 km sur le terrain.
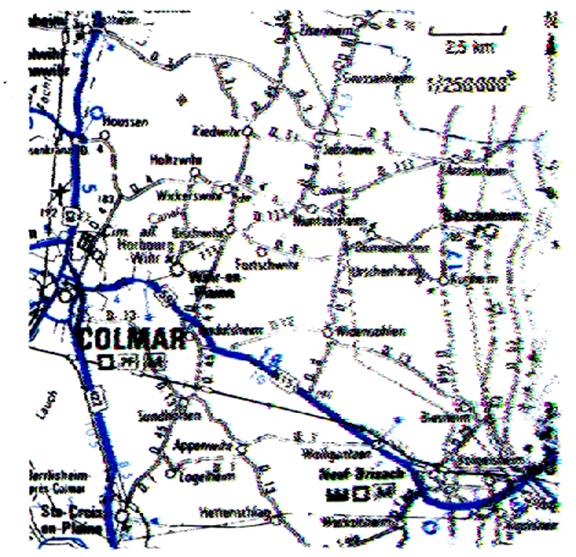
Cartes routières au 1 / 250 000 Une longueur de 250 000 cm sur le terrain est représentée par 1 cm sur la carte. 1cm sur la carte représente donc 2,5 km sur le terrain.
Cartes routières au 1 / 100 000 Une longueur de 100 000 cm sur le terrain est représentée par 1 cm sur la carte. 1cm sur la carte représente donc 1 km sur le terrain.
Cartes d’état-major au 1 / 80 000 Une longueur de 80 000 cm ( ou 800m) sur le terrain est représentée par 1 cm sur la carte. 1,25 cm sur la carte représente donc 1 km sur le terrain.
Cartes ONF au 1 / 25 000 Une longueur de 25 000 cm ( 250 m ) sur le terrain est représentée par 1 cm sur la carte. 1cm sur la carte représente donc 250 m sur le terrain.
Cartes ONF au 1 / 10 000 Une longueur de 10 000 cm ( 100 m ) sur le terrain est représentée par 1 cm sur la carte. 1cm sur la carte représente donc 100 m sur le terrain. Il existe des cartes aux 1/20000 et 1/5000
Les plans cadastraux : ils sont à l’ échelle 1/2500 ou 1/1000 Dans le premier cas , 1cm sur le plan représente 25 m sur le terrain et dans le deuxième cas , 1 cm sur le plan représente 10 m sur le terrain.

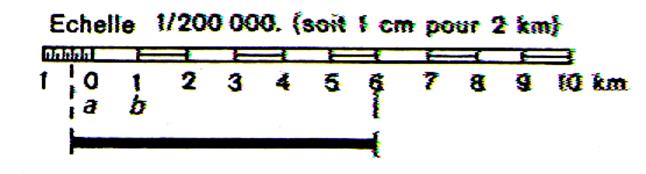
Echelle graphique 1/200 000

A propos d ‘ agrandissement ou de réduction ou « vraie grandeur »

1 ) nous faisons un agrandissement , si le rapport « Dimension du plan » (notée : Dp) sur « Dimension réelle » (notée : Dr) est supérieure à 1

(traduction mathématique : si > 1 alors « agrandissement »)

2 ) nous faisons une réduction , si le rapport Dp sur Dr est inférieure à 1

(traduction mathématique : si < 1 alors « réduction »)

3 ) nous faisons une représentation en vraie grandeur si le rapport Dp sur Dr est égal à 1

(traduction mathématique : si = 1 alors la représentation est dite «vraie grandeur » 

Travaux auto formatifs :

CONTROLE :

Donner la relation mathématique qui lie l’échelle , la dimension du plan et la dimension réelle.

1. Sous forme littérale

2. Sous la forme d’une formule.

EVALUATION :

Course d’orientation :

1°) La distance entre deux balises est de 1,5km ;quelle est la longueur que l’on doit mesurer sur un plan au 1/10 000 ?

2° ) La distance entre deux points est de 12,5 cm sur une carte au 1/20000 , quelle est la distance qui sépare ces deux balises ?

Sachant qu’un individu fait 60 « double pas » pour parcourir 100 m , combien doit-il compter de « double pas » avant d’avoir l’espoir d ‘apercevoir la balise ?