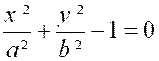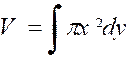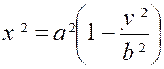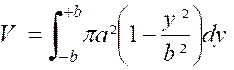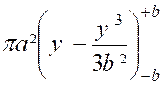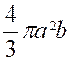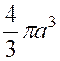les intégrales : application géométriques des intégrales simple: les volumes de révolution

	COURS

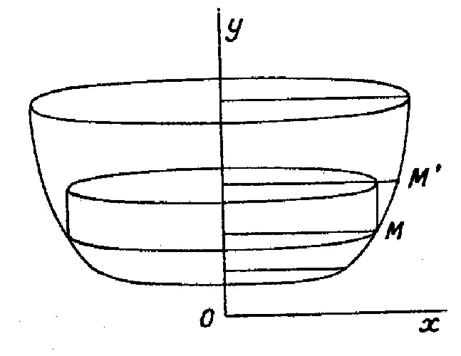
	Soit une courbe « » qui tourne autour de l’axe « 0y » . (voir figure ci contre). Cette courbe engendre une surface de révolution . On va calculer de volume limité par cette surface et deux plans perpendiculaires , sur l’ axe « Oy ». Par deux points « M » et « M ’ » , infiniment voisins, de la courbe donnée, menons deux plans perpendiculaires su l’axe « 0y ». Entre eux se trouve une petite partie du volume à évaluer et nous pouvons ( info rappel) sans grande erreur,remplacer ce petit volume par un cylindre de révolution ayant pour axe « Oy » , pour rayon de base l’abscisse « x » du point « M » et pour hauteur la différence « dy » entre les ordonnées des points « M » et « M ’ »
	L’élément de volume a donc pour valeur : « » Cette intégrale étant calculée entre les limites imposées par l’énoncé.

	Exemple :

	Voir : l’intégrale conduit au calcul du volume de la sphère…

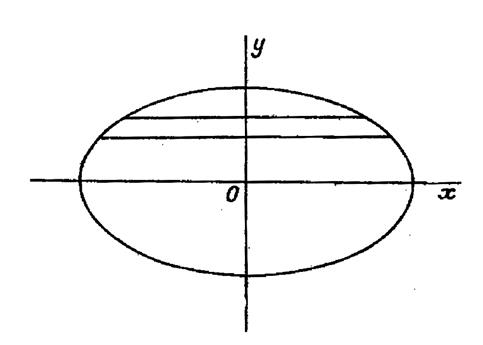
	Calculer le volume de l’ellipsoïde de révolution engendré par l’ellipse. en tournant autour de l’axe « Oy » (voir la figure ci contre.) Le volume est donné par l’intégrale :
	D’après l’équation de l’ ellipse , nous avons : par suite : = = Remarque : Si ,en particulier,on pose « b=a » , l’ellipse devient un cercle et on retrouve le volume de la sphère :



	CE qui termine ce cours…………..


	TRAVAUX AUTO FORMATIFS.

	CONTRÔLE
	Voir le cours !!!!!

	EVALUATION :
	calculer :
	Reprendre chaque exercice du cours.










	Voir le cours !!!!!