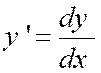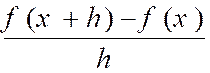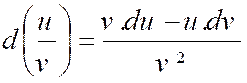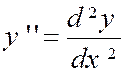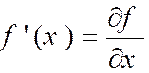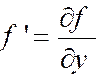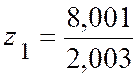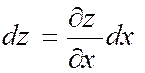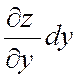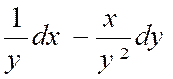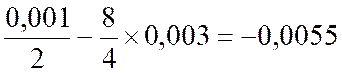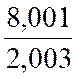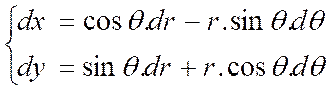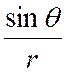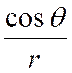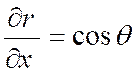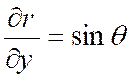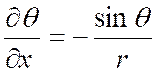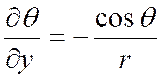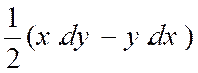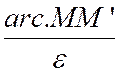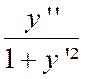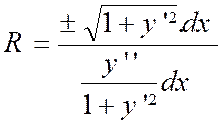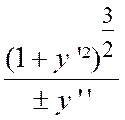Pré requis:

Info : liste des connaissances en algèbre préparant au même concours.
Fonctions (présentation )
Fonction : devoirs sur les pré requis

ENVIRONNEMENT du dossier:

Index warmaths

AVANT :

1°)Les dérivées.(sommaire).

2°) Les fonctions primitives

COURS

APRES :

Liste des chapitres traités

Le calcul intégral.

Complément d’Info :

1°) Liste des cours : prépa concours

A consulter pour compléments :

2°) les études de fonctions.

3°)Suite : Module sur les primitives et les intégrales

TITRE :niveau III : LES DIFFERENTIELLES.



	1. Différentielle première d’une fonction d’une variable indépendante.
	2. Signification géométrique de la différentielle première.
	3. Calcul d’une différentielle.
	4. Calcul d’une différentielle d’une somme .
	5. Calcul de différentielle d’un produit.
	6. Calcul de différentielle d’un quotient.
	7. Différentielle seconde d’une fonction d’une variable.
	8. Différentielle première d’une fonction de plusieurs variables.
	9. Représentation géométrique de la différentielle première d’une fonction de deux variables.
	10. Emploi de la différentielle totale pour le calcul des dérivées partielles.
	11. Exemples géométriques de différentielles.
	A ) Arc de courbe plane :
	B ) Aire plane :
	C ) Aire d’un secteur.
	D) Volume de révolution.
	E) Aire de révolution.
	F ) Variation de longueur d’un segment dont les extrémités décrivent deux courbes données.
	Exemples : 1°) Courbes parallèles. ; 2°) Propriété de l’arc de développée.
	13. Courbure. ( et l’angle de contingence)
	14. Calcul du rayon de courbure .


TEST	Contrôle	évaluation	Contrôle	évaluation

COURS

	1- Différentielle première d’une fonction d’une variable indépendante.
	Soit la fonction « y = f (x) » On appelle « différentielle première » de cette fonction le produit de sa dérivée par un accroissement arbitraire « h » donné à la variable « x » , soit l’écriture : « *d y = h f ‘* (x) = h y ’** »
	Si , en particulier, nous appliquons cette définition à la fonction « y = x » , nous avons alors « y ‘ = 1 », et par suite « d x = h »
	Convenons de prendre « h = d x » dans tous les cas nous obtenons ainsi une nouvelle forme de la différentielle : « d y = y ‘ d x » D’où : (on retiendra que : )
Q ..?	La différentielle d’une fonction est le produit de sa dérivée par la différentielle de la variable.
	C’est de là que vient la notation : « » qui sert à désigner la dérivée de « y » par rapport à « x ».
	Remarque : Il est intéressant d’expliquer comment on est conduit à la convention « h = d x » Supposons que « x » soit lui-même une fonction « g ( t ) » d’une autre variable « t » et soit « k » l’accroissement qu’il faut donner à « t »pour que « x » prenne l’accroissement « h ». La fonction « y = f (x) » devient une fonction de « t », soit « F( t ) » , dont la différentielle de « y = F( t ) » est par définition : « d y = k F ‘ ( t ) » La même définition entraîne que : « d x = k g ‘ ( t ) ». D’autre part , d’après le théorème donnant la dérivée d’une fonction de fonction , on a : « F ‘ ( t ) = f ‘ ( x ) g ‘ ( t ) » Par suite : « d y = f ‘ ( x ) . k g ‘ ( t ) » « d y = f ‘ ( x ) . d x » En comparant : avec : « *d y = h f ‘* (x) » on voit bien que : « h = d x »**
	2. Signification géométrique de la différentielle première.
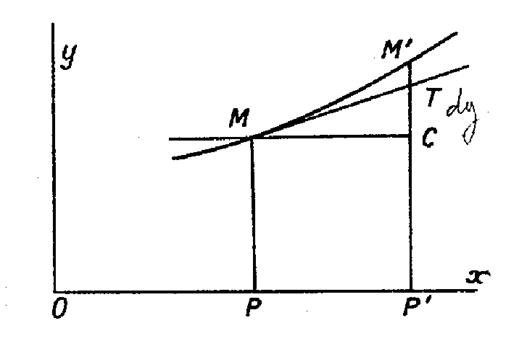
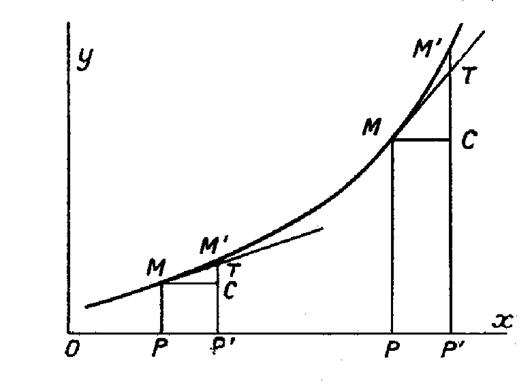
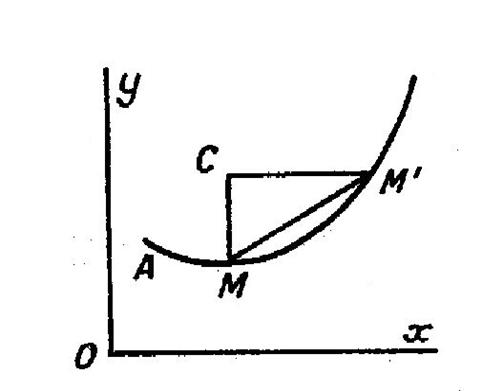
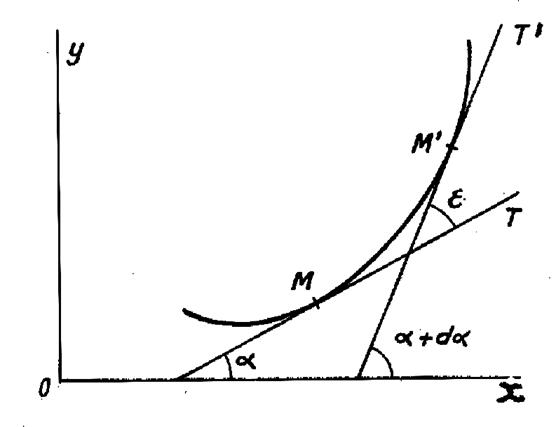
	Traçons la courbe représentant les variations de la fonction : « y = f ( x ) ». Soit « M » le point d’abscisse « = x » ; et « M ’ » le point d’abscisse « = x + d x ». Menons la tangente « MT », en « M », à la courbe et soit « T » son intersection avec « P ‘ M’ ». Enfin , soit « MC »la parallèle à l’axe « O x » menée par « M » . L’angle « CMT » a pour tangente la dérivée « y ‘ », de sorte que : « CT = MC . tan ()= y ‘ d x = d y »
	D’où : ( on retiendra que : )
	La différentielle représente l’accroissement d’ordonnée sur la tangente.
	Elle constitue une valeur approchée de l’accroissement exacte « CM’ », de la fonction ; et l’erreur est d’autant plus petite que l’accroissement « dx » de la variable est lui-même plus petit. En effet, dans ces conditions, l’arc de courbe diffère de moins en moins de la tangente.
	Remarque : Ceci nous fait comprendre une autre définition de la différentielle première : La différentielle première est la partie principale de l’accroissement pris par la fonction quand on donne à la variable un accroissement infiniment petit.
	En effet, quand « P’ » tend vers « P » , la différence « TM’ » entre « dy » et l’accroissement « y » devient négligeable par rapport à « dy ». On peut encore dire : La dérivée « f ‘ ( x ) » est la limite du rapport : quand « h » tend vers zéro. Par suite : = ( :lire « epsilon ») · tendant vers zéro en même temps que « h » On a donc : « f ‘ ( x + h ) - f ‘ ( x ) = h . f ‘ ( x ) + h » Puisque « h » est infiniment petit par rapport à « h . f ‘ ( x ) » ; on voit donc que « h . f ‘ ( x ) » , différentielle de la fonction « f ( x ) », est la partie principale , ou valeur approchée de l’accroissement « f ‘ ( x + h ) - f ‘ ( x ) de la fonction « f ( x ) ».
Voir dérivée de x².	Exemple : soit « f ( x ) = x² » Posons « x = 4 » et « h = 0,001 » La différentielle de la fonction est : « d f = 2 x .h » = 2 fois. 4 fois . 0,001 = 0,008 L’accroissement exact de la fonction est « 4,001)² - 16 = 16, 008001 – 16 = 0,008001 La différence entre l’accroissement de « f ‘ ( x ) » et sa différentielle est : 0,008001- 0,008 = 0, 000 001 Cette différence est très petite vis-à-vis de la différentielle « d f ».
	3 – Calcul d’une différentielle.
	On obtient la différentielle d’une fonction « f‘ ( x ) » en multipliant sa dérivée par « d x »
	Exemple : soit « y = sin x » ; on a « y ‘ = cos x » et « d y = cos x . dx »
	4 – Calcul d’une différentielle d’une somme .
	Soit « y = u + v » , on sait que « y ‘ = u’ + v ’ » D’autre part : « d y = y ‘ . dx » ; « d u = u ‘ . dx » ; « d v =v ‘ . dx » , par suite , en multipliant par « dx » on a : « d y = d u + d v »


	5 – Calcul d’une différentielle d’un produit .
	D’après le même raisonnement , on a : « d ( u .v ) = u dv + v du »


	6 – Calcul d’une différentielle d’un quotient .
	On a de même : « »

	7- Différentielle seconde d’une fonction d’une variable.
	Soit : « dy = y ‘ dx » la différentielle première de la fonction « y ».
	Le second membre est un produit dont on peut prendre , à nouveau, la différentielle. Mais on voit sur la figure ci contre , que si l’on veut comparer entre elles les valeurs que prend la différentielle « CT » pour toutes les valeurs de « x » , il faut prendre pour « P P ‘ » une valeur indépendante de « x ». Cette valeur sert , pour ainsi dire, d’unité de mesure pour évaluer les différentielles. On obtient ainsi , ce qui est logique, une différentielle d’autant plus grande que la fonction croît plus rapidement . C’est pour cette raison que « dx » ne doit pas être différentié, de sorte que : « d (d y )= d y ‘ . d x » D’où : « d² y = y ‘ ’ dx . dx = y ‘ ’ ( dx )² » « d² y » s’appelle « la différentielle seconde de y » . On peut donc écrire : « d² y = y ‘ ’ dx ² » ce qui explique la notation : « » servant à représenter la dérivée seconde.
	8 – Différentielle première d’une fonction de plusieurs variables.
	Par définition , la différentielle première de la fonction « Z = f ( x ; y ) » est « d z = f ‘ (x ) d x + f ‘ y d y » et étant les dérivées partielles de « f » par rapport à « x » et « y » « d z » s’appelle aussi une différentielle totale . Ici encore « d z » est la partie principale de l’accroissement pris par « z » « d z quand on donne à « x » et « y » des accroissements infiniment petits . Bornons nous à une vérification numérique :
	Exemple : soit « z = » , pour « x = 8 » et « y = 2 », on a « z = 4 » Donnons à « x » l’accroissement « 0,001 » et à « y « l’accroissement « 0,003 » , de sorte que « z » prend la nouvelle valeur : ; la différence de « z » est : « + = = » D’autre part , l’accroissement exact de « z » est « = - 4 = 3 , 994 5082 – 4 = - 0, 005 491 8 » La différence entre l’accroissement et la différentielle est « = 0, 000 0082 . Elle est de l’ordre de « »
	9- Représentation géométrique de la différentielle première d’une fonction de deux variables.
	Info : géométrie dans l’espace … « voir : repérage d’un point dans l’espace » ..
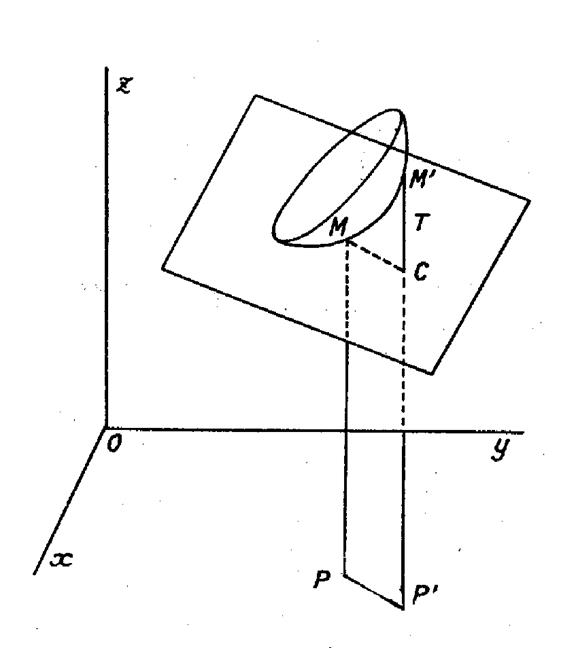
	Par rapport à trois axes orthogonaux , 0x , Oy , Oz (figure ci contre) l’équation « z = f ( x , y) »représente une surface.
	Cherchons à interpréter la différentielle. « dz = f ‘x dx + f ‘y dy » à l’aide du plan tangent , de même que nous avons utilisé la tangente à une courbe pour interpréter la différentielle d’une fonction d’une variable. Soit le point « M » projeté sur le plan « x0y »en « P » et « M’ » le point projeté en « P’ » de coordonnées ( x + dx ; y + dy ) . Menons le plan tangent , en « M » à la surface et soit « T »son intersection avec « P ‘ M ’ ». Enfin soit « MC » la parallèle à « P P ’ » menée par «M ». L’équation du plan tangent est : « Z – z = ( X – x ) f ‘ x + ( Y – y ) f ‘ y » « X , Y , Z » étant les coordonnées courantes. La cote « Z » du point « T » s’obtient en faisant : « X = x + dx » ; « Y = y – dy » D’où « Z – z = = f ‘x dx + f’ ‘ y dy = dz »
	Par suite : la différentielle représente l’accroissement de cote sur le plan tangent. Elle constitue une valeur approchée de l’accroissement « C M’ ». L’erreur devient négligeable quand « dx » et « dy » tendant vers zéro. En effet , la surface diffère alors de moins en moins du plan tangent.

	10 – Emploi de la différentielle totale pour le calcul des dérivées partielles.

	Soit « dz = f ‘x dx + f’ ‘ y dy » la différentielle d’une fonction « f ( x ; y ) » de deux variables indépendantes « x » et « y » . Supposons que , par un procédé quelconque , on ait mis « dz » sous la forme « d z = A dx + B dy ». En identifiant ces deux expressions de « dz » , on obtient : ( f ‘ x – A ) dx + ( f ‘ y – B) dy = 0 Cette identité a lieu quelle que soit la manière dont varient « x » et « y » , c'est-à-dire quelles que soient les valeurs de« dx » et de « dy » . Par suite : ( f ‘ x = A ) et ( f ‘ y = B) On obtient donc ainsi les dérivées de « f » par rapport à « x » et « y » .
	Exemple : Soient « r » et « » les coordonnées polaires d’un point dont les coordonnées cartésiennes sont « x » et « y » . Il en résulte que : « x = r . cos » ; « y = r . sin » Ces deux équations définissent implicitement « r » et « » en fonction de « x » et de « y » . Cherchons les dérivées partielles de « r » et de « » par rapport à« x » et « y ». En différenciant les deux équations précédentes , nous avons : résolvons ces équations par rapport à « dr » et « d ». Nous obtenons : « dr = cos .dx + sin .dy » « d= - dx + dy » D’après ce qui précède , on a : ; ; ;
	11 Exemples géométriques de différentielles.

	A ) Arc de courbe plane :
	Soient « M ( x ; y ) et « M’ ( (x + dx) ; ( y + dy)) deux points infiniment voisins d’une courbe plane ( voir ci contre). En appelant « s » l’arc « AM » , compté sur la courbe à partir d’une origine « A », l’accroissement « ds = M M’ » de l’arc diffère très peu de la corde « MM’ ». On peut donc écrire approximativement : « d s ² = ² = ² + ² = dx² + dy² » d’où la différentielle de l’arc. « ds = » Ce résultat obtenu en confondant l’arc et la corde, est d’autant plus approché que « M’ » est voisin de « M » . Il sera donc utilisable quand l’arc « MM’ » tendra vers zéro.

	Supposons maintenant la courbe définie en coordonnées polaires. ( voir la courbe ci dessous)
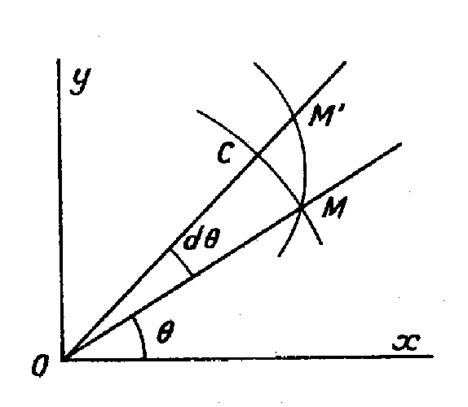
	Soient « r » et « » les coordonnées de « M » et « r + dr » et « et d » celles de « M ’ ». Le cercle de centre « O »et de rayon « OM » coupe « OM ‘ »en « C »et le petit arc de cercle « CM » peut être assimilé à un segment de droite perpendiculaire à « CM ‘ ». Par suite le triangle rectiligne « MCM ’ »est rectangle en « C »et « ² = ² + ² » d’autre part , le petit arc de cercle « CM » est égal au produit du rayon par l’angle au centre compté en radians. « CM = r d » et « C M ’ = dr » On a donc : « ² = d s ² = r ² d ² + d r ² »
	Remarque : Ce résultat peut se déduire du précédent . Soient « x ; y » les coordonnés cartésiennes de « M » , On a : « x = r . cos » ; « y = r . sin » Par suite et « d x² + dy² = ( cos .dr - r sin . d )² + ( sin .dr - r cos . d )² = dr² + r² d²
	B ) Aire plane :
	Considérons l’aire limitée par une courbe (voir figure ci-dessous)
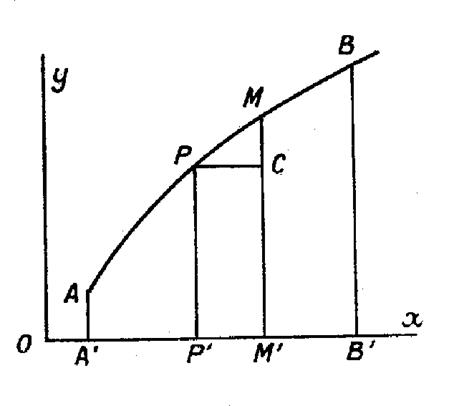
	L’axe « Ox » et deux parallèles « A’ A ; B ‘ B » à l’arc « 0y ». En partageant cette aire par des parallèles « P ‘ P » et « M’ M » à « Oy », on obtient un élément d’aire qui est un trapèze curviligne « P ‘ P M M ’ » Menons par « P » la parallèle « P C » à « O x ». Nous obtenons un rectangle « P ‘ P C M ’ »dont l’aire diffère très peu de l’aire du trapèze. Ce rectangle représente la différentielle de l’aire. Il a pour surface : « P ‘ P . P ‘ M’ = y dx »
	C ) Aire d’un secteur.
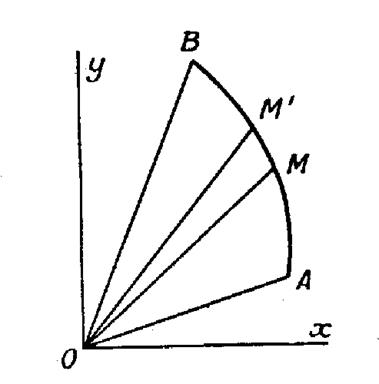
	L’aire d’un secteur « AOB » ( figure ci contre) limité par une courbe et deux rayons vecteurs , peut être décomposée en éléments tel que « M O M ’ ». Ce sont des triangles curvilignes , assimilables à des triangles rectilignes obtenus en remplaçant l’arc « M M ’ »par la corde. Pour avoir une valeur approchée de l’élément d’aire , c'est-à-dire sa différentielle, distinguons deux cas suivant la manière dont la courbe est définie.
	1°) En coordonnées cartésiennes , nous appelons « x » et « y » , les coordonnées de « M » et « x + dx » ; « y + dy » celles de « M’ » . L’aire du triangle « M O M ’ » est , au signe prés :
		O	0	1	=
		« x »	« y »	1
		« x + dx »	« y + dy »	1
	2°) En coordonnées polaires , soient « r » et « » les coordonnées de « M » et « r + dr » et « et d » celles de « M ’ ». l’aire du triangle « M O M ’ » est : « OM . O M’ .sin MOM ‘ = ( r + rd ) sin d » En négligeant « dr » vis-à-vis de « r » , et remplaçant le sinus par l’arc , nous obtenons la différentielle cherchée : « r ² d » Remarque : O peut déduire le second résultat du premier. En effet , en posant : « x = r cos . » et « y = r sin. » On a : « dx = cos dr – r sin d » ; « dx =sin dr – r cos d » d’où : « x dy – y dx = r cos. ( sin dr – r cos d ) - r sin ( cos dr – r sin d ) = r ² d »
	D) Volume de révolution.
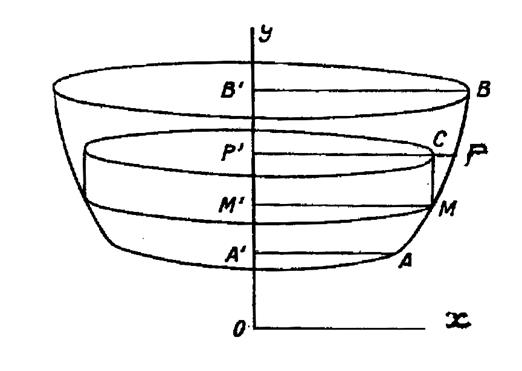
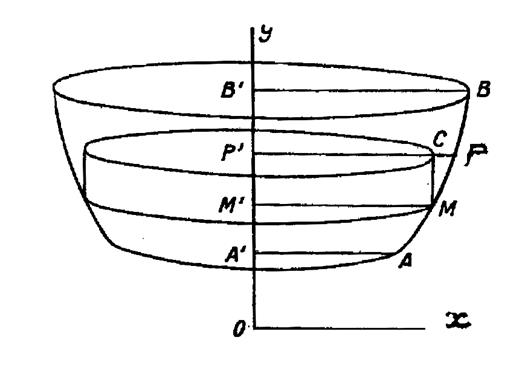
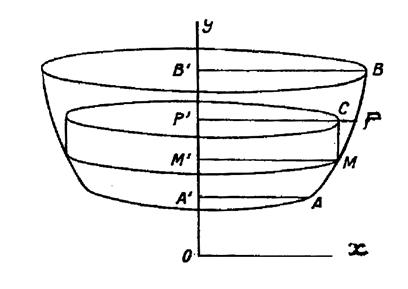
	Considérons une courbe « y » f( x ) qui tourne autour de l’axe « Oy » (voir ci contre). L’aire limitée par la courbe « 0y » et deux parallèles « A A ‘ » ; « B B ‘ »à « Ox »engendre un volume de révolution. Partageons ce volume par des plans infiniment voisins et perpendiculaires à « Oy » L’élément de volume , engendré par le trapèze curviligne « M’ M P P ‘ » peut être remplacé approximativement par le cylindre engendré par le rectangle « M’ M P P ‘ ». Le rayon de base du cylindre est « M’ M = x » Sa hauteur est « MC = dy » Son volume est la différentielle cherchée « d V = x² d y »

	E) Aire de révolution.
	Cherchons maintenant la différentielle de l’aire de révolution engendrée par la même courbe en tournant autour de « O y ». (voir ci contre) L’élément d’aire est une petite zone décrite par l’arc « MP ». Cette aire est assimilable à l’aire du tronc de cône engendré par la corde « M M’ ».( On commettrait une erreur en prenant l’aire du cylindre engendré par « MC »).
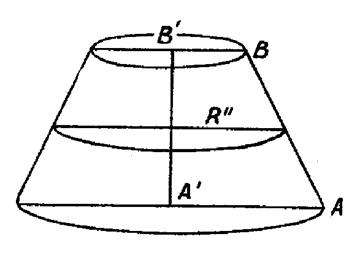
	Rappelons que l’aire d’un tronc de cône est le demi-produit de la somme des circonférences de base par l’ apothème. « ( A ‘ A + B ‘ B) AB = ( R + R ‘ ) a » ( voir la figure ci contre) ou encore , en appelant « R ‘ ’ »la rayon d’une section équidistante des bases, de sorte que « R + R ‘ = 2 R ‘ ’ » , on obtient pour surface « 2 R ‘ ‘ a »
	Dans le cas actuel ( voir ci contre ) R ‘ ‘ est l’abscisse « x » du point « M » et « a » est l’élément d’arc « ds = MP » de la courbe génératrice. Exactement , R ‘ ‘ = x + », mais « » est négligeable vis-à-vis de « x », l’élément d’aire est donc : « »
	F ) Variation de longueur d’un segment dont les extrémités décrivent deux courbes données.
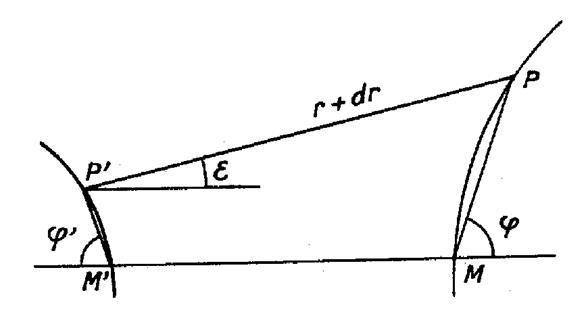
	Soit un segment de droite « M’ M »de longueur « r », dont les extrémités décrivent deux courbes données. ( ci contre). Quand les deux points « M » et « M’ » décrivent respectivement deux petits arcs « MP = ds » et « M ’ P ‘ = d s’ », le segment prend une nouvelle position « P ‘ P » , de longueur « r + d r » Soient d’autre par , « » et « ‘»les angles que font «MP » et « M ’ P ‘ » avec « M’ M ». Ce sont , à la limite, les angles que font avec « M’ M » les tangentes aux deux courbes. Projetons le contour polygonal « M ’ P ‘ MP » sur la droite « M’ M »et désignons par « » l’angle infiniment petit que fait « P ‘ P » avec « M’ M ». Nous obtenons : « r = - M’ P ‘ cos ’ + ( r + dr) cos - M P cos »
	D’autre part , « cos » est très voisin de « 1 » . D’une manière précise , « cos = 1 – 2 sin ² » et , quand « » tend vers zéro , « sin ² » est infiniment petit du second ordre puisqu’il est équivalent à « » On peut donc écrire : « r = - cos ’ ds’ + r + dr - cos ds» D’où finalement : « dr = - cos ds + cos ’ ds ‘ » Nous allons nous borner à deux applications de cette formule.
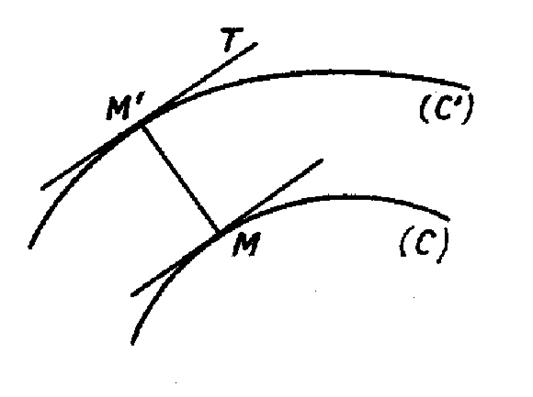
	1°) Courbes parallèles. Sur toutes les normales à une courbe ( C ) (figure ci contre) portons une longueur constante « M M’ = r » . Le lieu de « M ’ » est , par définition, une courbe ( C’) parallèle à « C ». Dans ce cas : « dr = 0 » ; « = » ; cos = 0 Par suite : cos ’ d s’ = 0 Comme « d s’ » n’est pas nul , on a « cos’ = 0 » et « ‘ = » M’ T’ » à la courbe ( C’) . Autrement dit : deux points correspondants « M » et « M ’ » , les deux courbes parallèles sont normales à la même droite « M M ’ »

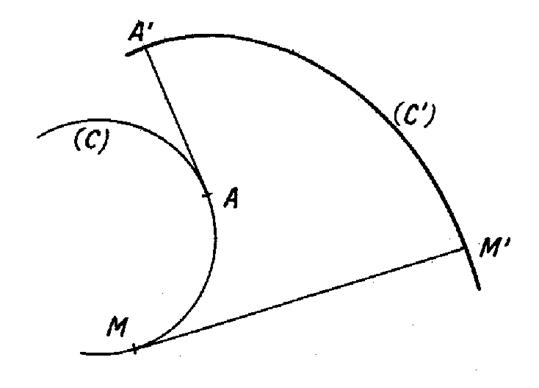
	2°) Propriété de l’arc de développée. Soit « C » la développée d’une courbe « C’ » c’est à dire l’enveloppe de ses normales ( voir ci contre) . Le segment « M M ’ » de longueur « r » , fait avec la courbe « C » en « M » , un angle nul et avec la courbe « C’ » en « M ’ », un angle droit. Par suite , « cos = 1 » , « cos ‘ = 0 » et la formule précédente se réduit à « dr = ds » En intégrant , on a : « r – r ₀ = s – s ₀ » ; « r ₀ et s ₀ » étant les valeurs de « r » et « s » pour une position particulière du segment « A A ‘ ». D’autre part : « r – r ₀ = M M ’ » et « s – s ₀ = arc AM», d’où : l’arc de développée est égal à la différence des longueurs des normales limitées à la courbe et à sa développée.
	12 – Courbure.
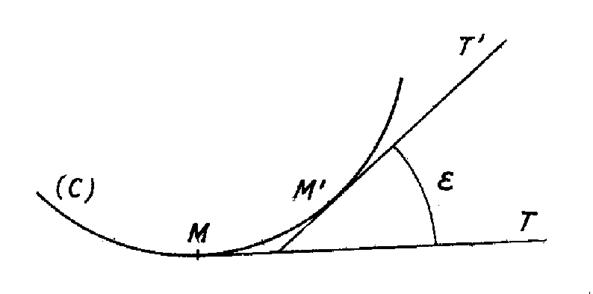
	Soit « M M ‘ »un petit arc « ds » d’une courbe « C » ( figure ci contre). Les tangentes « MT » et « M ’ T ’ » font entre elles un petit angle « » qu’on appelle l’angle de contingence. Le rapport « » tend , quand « M’ » tend vers « M », vers une limite qu’on appelle le rayon de courbure « R » en « M ». La courbure est « ».

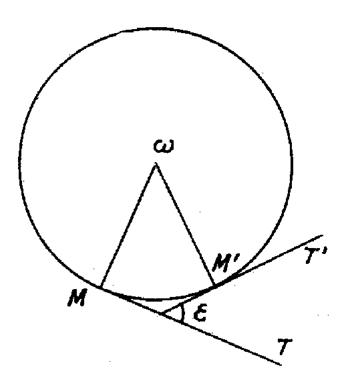
	Cette définition se comprend en considérant un cercle ( voir figure ci contre). L’angle de contingence est égal à l’angle « M M ’ » des deux rayons. On sait que l’arc « M M ’ » est le produit du rayon par la mesure de l’angle au centre, évalué en radian. Par suite : « Arc M M ‘= R » et « R = »

	Désignons par « » l’angle que fait avec « O x » la tangente « M T » (figure ci contre) La tangente voisine « M’ T’ »fait avec « O x »l’angle « + d » de sorte que « = d » Par suite : R = ; « R » est donc le rapport des différentielles de l’arc « s » et de l’angle « » , ou ce qui revient au même , « R » est la dérivée de « s » par rapport à « ».
	13 - Calcul du rayon de courbure .
	Soit une courbe « y = f (x ) » on sait que « ds = et que « dy= y ‘ dx » , on a : « ds = = » D’autre part, le coefficient angulaire de la tangente est égale à la dérivée, c'est-à-dire que « tan = y ’ » On a donc : « = arc tan y ’» Et : « d = d (arc tan y ’) = dx » D’après la façon dont on calcule une différentielle ( info ++) : Donc : = On choisit le signe devant « y ‘ ‘ » , de manière à obtenir pour « R » une valeur positive.
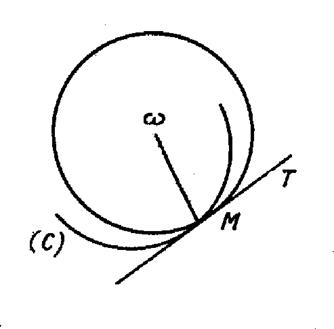
	Définition : Le cercle de courbure « » s’obtient en portant sur la normale , dans le sens de la concavité, une longueur égale à « R » (voir la figure ci contre) Le cercle de centre « »et de rayon « « M»est le cercle de courbure, ou cercle osculateur. C’est le cercle qui au point « M », a la même courbure que la courbe . On démontre que le cercle de courbure est la position limite d’un cercle qui est tangent en « M » à la courbe ( C )et qui passe par un point « M’ » de ( C ) infiniment voisin de « M »
	En général, la courbe ( C ) traverse , en « M », son cercle de courbure. Sur l’arc de courbe extérieur au cercle, la courbure est plus petite qu’en « M », sur l’arc intérieur au cercle la courbure est plus grande.


	CE qui termine ce cours…………..


	TRAVAUX AUTO FORMATIFS.

	CONTRÔLE
	Voir le cours !!!!!voir les définitions en « orange » !!!!!

	EVALUATION :
	Voir le cours !!!!!