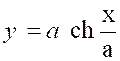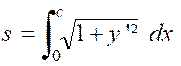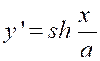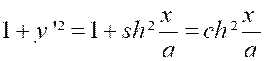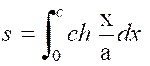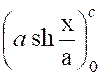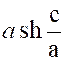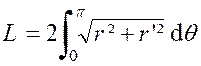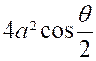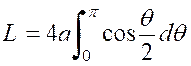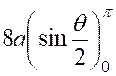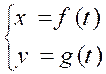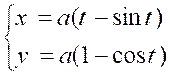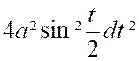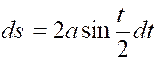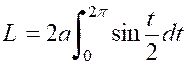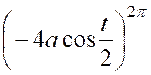Pré requis:
|
Info : liste des connaissances en algèbre
préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
|
AVANT :
2°) Le calcul intégral. (niveau 4) 4°) L’intégration par parties. 5°) application
géométrique d’une intégrale simple :aires
planes. |
APRES :
|
Complément d’Info :
1°) Liste des cours : prépa concours
A consulter pour compléments : |
TITRE :niveau
III : LES INTEGRALES : APPLICATIONS GEOMETRIQUES DES INTEGRALES
SIMPLES :
ARC D’UNE COURBE PLANE.
|
|
|
|
|
|
· Préambule. « Rectifier une courbe » ;
« Quadrature d’une aire » ;
« Cubature d’un solide » |
|
|
|
1° )L’équation de la courbe
est de la forme : |
|
|
|
2°) La courbe est définie en coordonnées
polaires. |
|
|
|
3°) La courbe est définie par des équations
paramétriques. |
|
|
|
|
|
|
|
|
|
|||
|
Voir
l’évaluation !!! |
|
Contrôle |
évaluation |
||
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
« Rectifier
une courbe » On dit que l’on
« rectifie » une courbe lorsqu’on en cherche la longueur. Cette façon de parler signifie que l’on cherche
une longueur, un segment rectiligne, équivalente à la longueur de l’arc de
courbe. |
|
|
|
|
« Quadrature
d’une aire » : |
|
|
|
|
On appelle souvent « quadrature d’une
aire » la mesure de sa surface ; cela correspond à la recherche
d’un carré ayant une aire équivalente. |
|
|
|
|
« Cubature
d’un solide » |
|
|
|
|
On appelle « cubature d’un solide » la
mesure de son volume , cela correspond à la
recherche d’un cube ayant un volume équivalent. |
|
|
|
|
|
|
|
|
|
D’une manière générale ,
l’élément d’arc « ds » est donné par la
relation : |
|
|
|
|
Plusieurs cas sont à distinguer suivant la
manière dont la courbe est définie. |
|
|
|
|
1°) L’équation de la courbe est de la forme : |
|
|
|
|
Dans ce cas « Par suite , l’élément d’
arc est , au signe prés : Exactement : Cette valeur de « ds »
exprimée sans double signe est valable
si « dx » et « ds » sont de
même signe, c'est-à-dire si on prend comme « sens positif» des
arcs le sens pour lequel l’abscisse
« x » va en croissant. |
|
|
|
|
|
|
|
|
|
Exemple : |
|
|
|
|
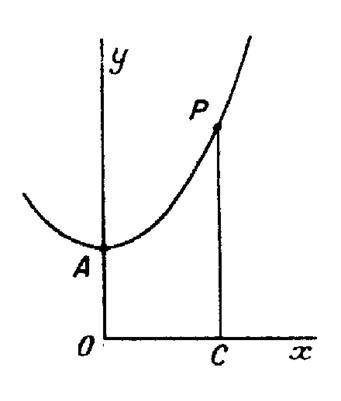
Vérifier la chaînette « Soit
« AP » l’arc limité au sommet « A » et à un point
« P » d’abscisse « c » Il a pour valeur :
On a « Par suite : « |
|
|
|
|
|
|
|
|
|
2°) La courbe est définie en coordonnées polaires. |
|
|
|
|
Dans ce cas l’élément d’arc est : ( voir rappel info) |
|
|
|
|
« |
|
|
|
|
Exemple : |
|
|
|
|
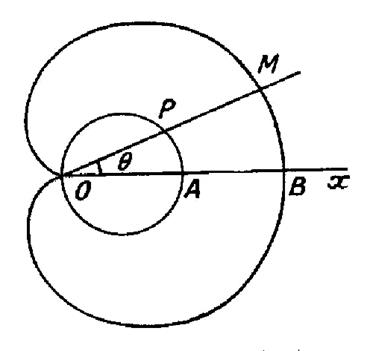
Longueur d’une cardioïde : La
cardioïde a pour équation : On l’obtient en construisant d’abord un cercle de
diamètre « OA = a » et en
partant sur chaque rayon « vecteur » « OP » une longueur
« P M = a ». Par symétrie, la longueur totale est le double de
l’arc « BMO »obtenu lorsque « « or « et «
par suite :
|
|
|
|
|
3°) La courbe est définie par des équations paramétriques. |
|
|
|
|
et par suite : « |
|
|
|
|
Exemple |
|
|
|
|
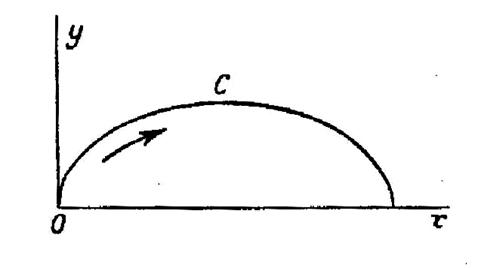
Calculer la longueur de la cycloïde
. ( voir figure ci contre)
et = « |
|
|
|
|
Par suite , en comptant
les arcs positivement dans le sens des « x » croissants : « La courbe « OCB » est obtenue ,toute entière , quand « t » varie
de « 0 » à « 2 « |
|
|
|
|
Remarque : On sait que la cycloïde est engendrée par un point d’une
circonférence de rayon « a » qui roule sans glisser sur « Ox ». ( voir comme exemple :Une cycloïde
est la trajectoire de la valve
d’une roue de vélo , lorsque la roue effectue un tour .) |
|
|
|
|
|
|
|
|
|
CE qui termine ce cours………….. |
|
|
|
|
|
|
|
||
|
|
TRAVAUX AUTO FORMATIFS. |
||||
|
|
|
|
|||
|
|
CONTRÔLE |
|
|||
|
|
Voir le cours !!!!! |
|
|||
|
|
|
|
|||
|
|
EVALUATION :
|
||||
|
|
calculer : |
|
|||
|
|
Reprendre chaque exercice du cours. |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Voir le cours !!!!! |
|
|||