Pré requis:
|
Fonction généralités (présentation ) |
ENVIRONNEMENT du dossier:
|
Objectif précédent |
Objectif suivant |
DEVOIR :contrôle des connaissances
|
|
|
|
|
|
|
|
|
|
1°)fonction application (définitions) |
I )
TRADUIRE :
a) f : N![]() R
R
x ![]() 2, 5 x
2, 5 x
lire :
Il y a fonction de l’ensemble N
(entiers naturels) vers l’ensemble R (réels) où « x » à pour
image 2,5 x
b ) f :
N ![]() D
D
x ![]() 3x +2
3x +2
lire :
Il y a fonction de l’ensemble N
(entiers naturels) vers l’ensemble D (décimaux) où « x » à pour
image 3 x +2
c)
f : R ![]() R
R
x ![]() 2x2 +3x
-1
2x2 +3x
-1
lire : Il y a
fonction de l’ensemble R (réels) vers
l’ensemble R (réels) où « x » à pour image 2x2 +3x -1
Dire si la relation qui existe entre les éléments de l’ensemble E et
les éléments de l’ensemble F est une fonction , et une application .
Justifier votre réponse .
on donne x Î E et
y Î
F
N°1
|
x |
62 |
79 |
124 |
156 |
163 |
182 |
195 |
|
y |
33 |
45 |
57 |
87 |
96 |
135 |
167 |
C’est une fonction ; chaque élément de l’ensemble de départ a une
image dans l’ensemble d’arrivée, (au plus).C’est une application puisque c’est
une fonction et que chaque élément a une image dans l’ensemble d’arrivée.
N°2
|
x |
62 |
79 |
124 |
156 |
163 |
182 |
195 |
|
y |
33 |
45 |
|
87 |
96 |
135 |
167 |
C’est une fonction ;chaque élément de l’ensemble de
départ a une image dans l’ensemble
d’arrivée., ce n’est une application .
N°3
|
x |
62 |
79 |
124 |
156 |
163 |
182 |
195 |
|
y |
33 |
45 |
57 |
87 ;135 |
96 |
|
167 |
Ce n’est pas une fonction ;l’
élément « 156 »de l’ensemble de départ a deux images
dans l’ensemble d’arrivée.
N°4
|
x |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
y |
7 |
7 |
9 |
11 |
15 |
17 |
19 |
C’est une fonction ; chaque élément de l’ensemble de départ a une
image dans l’ensemble d’arrivée, (au plus).C’est une application puisque c’est
une fonction et que chaque élément a une image dans l’ensemble d’arrivée.
N°5
|
x |
0 |
1 |
2 |
3 |
7/5 |
8 |
2 |
|
y |
2 |
3 |
2 |
5 |
7 |
3 |
5 |
N°6
|
x |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
y |
7 |
|
9 |
11 |
15 |
17 |
19 |
C’est une fonction ; chaque élément de l’ensemble de départ a une
image dans l’ensemble d’arrivée, (au plus).Ce n’est pas une application puisque
l’élément 8 n’a pas une image dans l’ensemble d’arrivée.
|
2°)fonction
« équation » |
identifier les fonctions suivantes :
y =
3x ; fonction linéaire
y =
-2x ; fonction linéaire
y = x2 +2x +1 fonction
du second degré
y= -x+1 fonction
affine
y = - x fonction
linéaire
y = (2/3) x fonction
linéaire
y = (12 /100) x fonction
linéaire
y = 2x2 +3x +5 fonction du
second degré
y = x fonction
linéaire
y = -2x2 +4x +2 fonction
du second degré
y = 3x +5 fonction
affine
y = -4x2 +x +7 fonction du second degré
y =0,3 x
+7 fonction affine
y = 15 x
+350 ; fonction affine
|
3°)fonction
« tableau de
variation » |
Soit
"x" un "réel"
quelconque .A chaque valeur de "x" on fait correspondre son image y =
3 x2
Compléter le tableau :
|
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
12 |
3 |
0 |
3 |
12 |
27 |
48 |
V )
Soit "x" un "réel" quelconque .
A chaque valeur de "x" on fait
correspondre son image y = -3 x +2
Compléter le tableau :
|
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
8 |
5 |
2 |
-1 |
-4 |
-7 |
-10 |
VI )
Soit "d" un réel tel
que : 0 £ d £ 5
A chaque valeur de d , on fait correspondre le réel p tel que p = 6,28 ![]() d
d
Compléter le tableau :
|
d |
0 |
1 |
2 |
3 |
4 |
5 |
|
p |
0 |
6,28 |
12,56 |
18,84 |
25,12 |
31,40 |
VII ) Soit "x" un nombre réel quelconque.
A chaque valeur de "x" faire correspondre
son double y
a) On appelle f cette fonction . Donner f(x) = 2x
b) Compléter le tableau:
|
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
5 |
|
y |
-4 |
-2 |
0 |
2 |
4 |
6 |
10 |
|
4°)fonction
« graphe » |
Les graphes
G1 ; G2 ; G3 ; G4 ; G5
; G6 représentent - ils
chacun une fonction ? Justifier votre réponse .
|
Graphes: |
O ou N |
justification |
|
G 1 = |
O
|
G
représente le graphe d ' une fonction , parce que chaque valeur du couple de points à une
seule valeur. |
|
G2 = |
N |
G
ne représente pas le graphe d ' une fonction , parce que la valeur "3" possède 2 valeurs
4 et 5. |
|
G3
= í( |
O |
G
représente le graphe d ' une fonction , parce que chaque valeur du couple de points à une
seule valeur. |
|
G4
= |
N |
Parce que « 5 » à deux
images. |
|
G5
= |
N |
Parce que « 7 » à deux
images. |
|
G6
= |
O |
G
représente le graphe d ' une fonction , parce que chaque valeur du couple de points à une
seule valeur. |
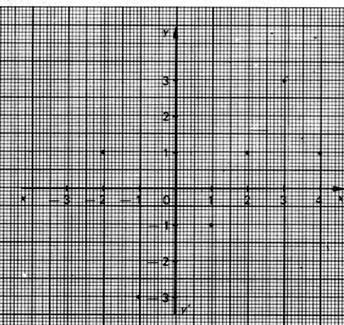
2°) On donne la représentation
graphique de la fonction « g » , donner son graphe.
G =í
(-4,3 ;-0,3) ;(-2 ;-1) ;(-1 ;-3) ; (+1 ; -1
) ;(+2 ; +1 ) ; (+3 ; +3 ) ;(+4 ;+1) ý
|
|
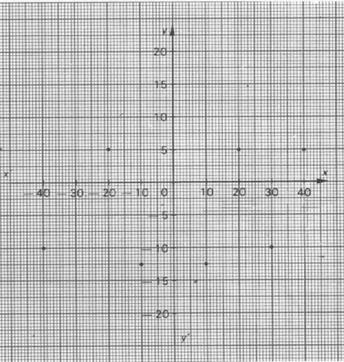
3°) On donne la représentation
graphique de la fonction « f » , donner son graphe.
G =í (-10 ;-40) ;
(-20 ;+5) ;(-10 ;-12,5) ;(+1 ;-12,5) ;(+20 ;+5) ;(+30 ;-10) ;(+40 ;+5)
ý
|
|
|
5°)fonction
« représentation graphique» |
Faire les représentations graphiques
des fonctions représentées par les équations données :
|
Faire la représentation graphique de la fonction : y =
3,5x |
Réponse : construction d’un tableau de variation :
|
|
A |
B |
O |
C |
D |
E |
|
« x » |
-2 |
0 |
0,4 =(3/7) |
0,75 (3/4) |
2 |
5 |
|
« y » |
-7 |
0 |
1,5 |
2,6 |
7 |
17,5 |
|
Voir la représentation
graphique |
|
Faire la représentation graphique de la fonction : y =
-2x+1
Réponse : construction d’un tableau de variation :
|
|
A |
B |
O |
C |
D |
E |
|
« x » |
-2 |
-1 |
0 |
+1 |
+2 |
|
|
« y » |
5 |
3 |
1 |
-1 |
-3 |
|
Faire la représentation graphique de la fonction : y = 3x![]()
Réponse : construction d’un tableau de variation :
|
|
A |
B |
O |
C |
D |
E |
|
« x » |
-2 |
-1 |
0 |
+1 |
+2 |
|
|
« y » |
12 |
3 |
0 |
3 |
12 |
|
On prendra le plus de valeur possible pour « x » , afin
d’avoir un maximum de points ,pour permettre d’avoir un tracé précis.
Faire la représentation graphique de la fonction : y =
-3x![]() +2x -1
+2x -1
Prendre le plus de points possible.