Pré requis:
|
|
|
|
Fonction affine (info ) |
|
|
Représentation graphique d’une droite dans un repère
cartésien |
Environnement du
dossier
|
Objectif précédent : 3°)
Résoudre une équation de la forme ….. |
|||
|
|
|
|
|
DOSSIER : EQUATION
d'une fonction
affine : forme y = m x + p
|
TEST |
COURS |
Interdisciplinarité |
|
|
|
COURS
|
|
|
|
|
L’équation d’une fonction affine est toujours de la forme : |
|
|
|
|
I
) Activités : savoir rechercher
une équation. |
|
|
|
|
Activité 1 : Trouver une équation d’une
droite ( D) passant par un point et dont on connaît
le coefficient directeur de (D) |
|
|
|
|
Enoncé 1 |
|
|
|
|
Trouver une équation d’une droite ( D) passant
par un point A ( -3 ; 1) et dont
le coefficient directeur de (D) est
– 4 . |
|
|
|
|
Solution : |
|
|
|
|
Tracer (D) |
|
|
|
|
(D) à pour équation la forme :
on
connaît « m » ; donc (1) |
|
|
|
|
|
|
|
|
|
Recherche de « p » : La droite passe par « A » ; Quand
« On remplace dans l’équation (1) :
on
résout l’équation : p = 1
–12 p =
-11 |
Il faut
résoudre la forme :
|
|
|
|
|
|
|
|
|
Conclusion : (D) à pour équation : |
|
|
|
|
|
|
|
|
|
Activité 2 : Trouver une
équation d’une droite ( D) passant par deux
points dont on connaît les
coordonnées. |
|
|
|
|
Enoncé 2 : Soit une droite (D’) la droite passant un point A’ de coordonnées ( -2 ;3 ) et par le
point B de coordonnées ( 1 ; 4 ) |
|
|
|
|
Solution : |
|
|
|
|
L’équation de la droite est de la forme |
|
|
|
|
Pour
A’ : Pour
B :
|
|
|
|
|
|
|
|
|
|
Les deux égalités doivent être vérifié par «
|
Info plus : résoudre
un système de deux équations à deux inconnues |
|
|
|
|
|
|
|
|
L’équation 3 = -2 (1)
( 2
) l’équation devient
par transformation |
|
|
|
|
|
|
|
|
|
On remplace dans l’équation ( 2) ,
D’où
|
|
|
|
|
|
|
|
|
|
Si
|
|
|
|
|
La droite ( D’) a donc pour équation :
|
A vérifier par un tracé. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Activité 3 : Trouver une équation d’une droite
( D) passant par deux points dont on connaît les coordonnées.Cas
particulier d’une droite parallèle à l’axe des ordonnées. |
|
|
|
|
|
|
|
|
|
Enoncé 3 : Soit la droite ( D’’) passant par
les points E ( 3 ; 4 ) et F ( 3 ;-2 ) |
|
|
|
|
|
|
|
|
|
Solution : |
|
|
|
|
1°) tracer ( D’’) |
|
|
|
|
|
|
|
|
|
2°) Analyse du tracé : |
|
|
|
|
Quelles sont les coordonnées du projeté
de « E » sur ( O J) selon ( OI ) ? |
|
|
|
|
|
|
|
|
|
Quelles sont les coordonnées du projeté
de « F » sur ( O J) selon ( OI ) ? ( même
projection) |
|
|
|
|
|
|
|
|
|
Quelles sont les coordonnées du projeté
de tous les autres points de la droite
passant par « E » et « F » sur ( O J) selon ( OI ) ? |
|
|
|
|
|
|
|
|
|
Constat : on constate que la droite ( EF) est
constituée de tous les points ayant pour abscisse « 3 » et qu’il n’y a que ces points sur (EF)
|
|
|
|
|
Activité 4 : |
|
|
|
|
Cas particulier d’une droite parallèle à l’axe des ordonnées. |
|
|
|
|
Soit la droite ( MN) passant par les points M ( 2 ; - 4 )
et N ( 5 ;-4 ) |
|
|
|
|
|
|
|
|
|
1°) tracer ( MN) |
|
|
|
|
|
|
|
|
|
2°) Analyse
du tracé : |
|
|
|
|
|
|
|
|
|
Quelles sont les coordonnées du projeté
de « M » sur ( O I) selon ( OJ ) ? |
|
|
|
|
|
|
|
|
|
Quelles sont les coordonnées du projeté
de « N » sur ( O I) selon (
OJ ) ? ( même projection) |
|
|
|
|
|
|
|
|
|
Quelles sont les coordonnées du projeté
de tous les autres points de la droite
passant par « M » et « N » sur ( O I) selon ( OJ ) ? |
|
|
|
|
|
|
|
|
|
Constat : on constate que la droite ( MN)
est constituée de tous les points ayant pour ordonnée « -4 » et qu’il n’y a que ces points sur (MN) y = - 4 est une équation de la
droite (MN) |
|
|
|
|
On retiendra la propriété suivante : Toute droite non parallèle à l’axe des ordonnées a une équation du
type : Toute droite passant par deux
points de même abscisse
« p » est parallèle à l’axe des ordonnées et a pour équation : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO - FORMATIFS
.
1° ) Donner la procédure permettant de trouver
une équation d’une droite ( D) passant par un point et dont on connaît le coefficient directeur de (D).
2°) Donner la procédure permettant
de trouver une équation d’une droite
(D’) passant deux
points dont on connaît les coordonnées .
EVALUATION:
1° ) Trouver une équation d’une droite ( D)
passant par un point A ( -3 ; 1) et
dont le coefficient directeur de (D) est
– 4 .
2°) Trouver l’équation de la
droite (D’) passant
un point A’ de coordonnées (
-2 ;3 ) et par le point B de coordonnées ( 1 ; 4 )
3°) Trouver l’équation
de la droite ( D’’) passant par les points E ( 3 ; 4 ) et F
( 3 ;-2 ) . ( passer par un tracé)
4°) Trouver
l’équation de la droite ( MN) passant par les points M ( 2 ; - 4 ) et
N ( 5 ;-4 ). (Passer par un tracé )
5°) Donner les équations des 3 droites. AB ;
BM ; AM
ensuite calculer les longueurs des côtés du triangle. 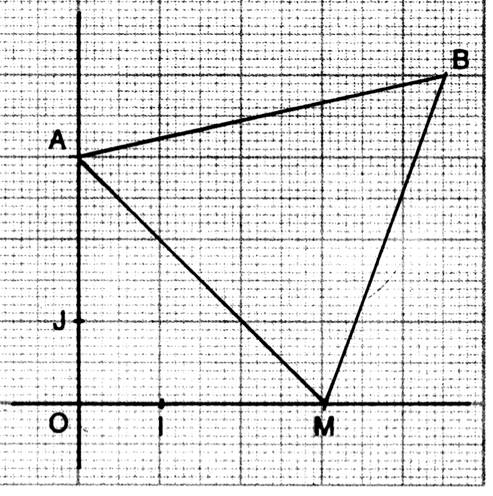
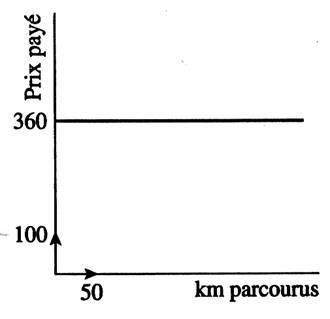
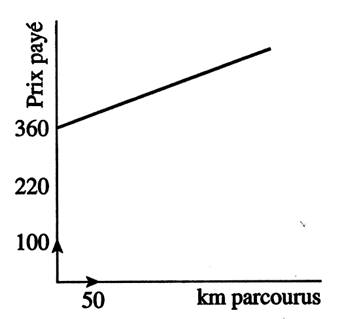
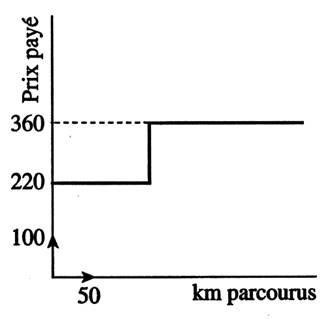
Exemple de
tracés : Interpréter ces tracés.
|
|
|
|
|
|
|
|
|
|
|
|
|
|